|
1 | 1 | --- |
2 | 2 | Title: '.log10()' |
3 | | -Description: 'Calculates the base-10 logarithm of each element in an array.' |
| 3 | +Description: 'Calculates the base-10 logarithm of input values element-wise.' |
4 | 4 | Subjects: |
5 | 5 | - 'Computer Science' |
6 | 6 | - 'Data Science' |
7 | 7 | Tags: |
8 | 8 | - 'Arrays' |
9 | | - - 'Methods' |
| 9 | + - 'Functions' |
| 10 | + - 'Math' |
10 | 11 | - 'NumPy' |
11 | 12 | CatalogContent: |
12 | 13 | - 'learn-python-3' |
13 | | - - 'paths/computer-science' |
| 14 | + - 'paths/data-science' |
14 | 15 | --- |
15 | 16 |
|
16 | | -In NumPy, the **`.log10()`** method is used to calculate the base-10 logarithm of each element in an array. It is primarily used in scientific computations and mathematical applications where logarithmic scaling is required. |
| 17 | +NumPy's **`.log10()`** function calculates the **base-10 logarithm** of input values element-wise. It computes the power to which 10 must be raised to obtain a given number. It’s a key tool for applying logarithmic transformations in numerical computing. |
| 18 | + |
| 19 | +The `.log10()` function is widely used in various fields such as data science, signal processing, and scientific computing. It helps visualize data spanning multiple orders of magnitude, simplifies multiplicative relationships into additive ones, and is crucial for applications like sound analysis (decibel calculations), pH measurements in chemistry, earthquake magnitude (Richter scale), and creating log-scale visualizations. |
17 | 20 |
|
18 | 21 | ## Syntax |
19 | 22 |
|
20 | 23 | ```pseudo |
21 | | -numpy.log10(array, out=None, where=True) |
| 24 | +numpy.log10(x, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True) |
22 | 25 | ``` |
23 | 26 |
|
24 | | -- `array`: An array-like structure containing the elements for which the base-10 algorithm will be applied. |
25 | | -- `out` (Optional): The array where the result is to be stored. If not provided, a new array is created to store the results. |
26 | | -- `where` (Optional): The condition (array of boolean values) that determines which elements will the method be applied on. |
27 | | - - If the condition is `True` for a particular element, the logarithm is computed for that element. |
28 | | - - If the condition is `False` for a particular element, the logarithm is not computed for that element and the original element is retained. |
29 | | - - If not provided, the logarithm is computed for all elements. |
| 27 | +**Parameters:** |
| 28 | + |
| 29 | +- `x`: Input array or scalar value for which to calculate the base-10 logarithm. |
| 30 | +- `out`(Optional): Output array to store results. Must have the same shape as the expected output. |
| 31 | +- `where`(Optional): Boolean array or condition specifying where to calculate the logarithm. |
| 32 | +- `casting`(Optional): Controls what kind of data casting may occur during the operation. |
| 33 | +- `order`(Optional): Memory layout for the output array. |
| 34 | +- `dtype`(Optional): Data type for the output. If not specified, the data type of the input is used. |
| 35 | +- `subok`(Optional): If `True`, allow subclasses of ndarray. |
| 36 | + |
| 37 | +**Return value:** |
30 | 38 |
|
31 | | -## Example |
| 39 | +The function returns an [ndarray](https://www.codecademy.com/resources/docs/numpy/ndarray) containing the base-10 logarithm of each element in `x`. For negative input values, it returns `NaN` (Not a Number). |
32 | 40 |
|
33 | | -The below example demonstrates the use of the `.log10()` method: |
| 41 | +## Example 1: Basic Usage of the `.log10()` method in NumPy |
| 42 | + |
| 43 | +This example demonstrates how to calculate the base-10 logarithm of various numbers using NumPy's `.log10()` function: |
34 | 44 |
|
35 | 45 | ```py |
36 | 46 | import numpy as np |
37 | 47 |
|
38 | | -result = np.log10([1e-15, -3., 10, 100]) |
| 48 | +# Create an array of values |
| 49 | +values = np.array([1, 10, 100, 1000]) |
| 50 | + |
| 51 | +# Calculate the base-10 logarithm |
| 52 | +result = np.log10(values) |
39 | 53 |
|
40 | | -print(result) |
| 54 | +# Display the result |
| 55 | +print("Original values:", values) |
| 56 | +print("Base-10 logarithms:", result) |
| 57 | + |
| 58 | +# Base-10 logarithm of a single value |
| 59 | +single_value = 10000 |
| 60 | +print(f"log10({single_value}) =", np.log10(single_value)) |
| 61 | + |
| 62 | +# Working with negative or zero values |
| 63 | +mixed_values = np.array([100, 10, 1, 0, -10]) |
| 64 | +print("Mixed values:", mixed_values) |
| 65 | +print("Base-10 logarithms (with warnings):", np.log10(mixed_values)) |
41 | 66 | ``` |
42 | 67 |
|
43 | | -The code above will generate the following output: |
| 68 | +The output generated by this code will be: |
44 | 69 |
|
45 | 70 | ```shell |
46 | | -[-15. nan 1. 2.] |
| 71 | +Original values: [1 10 100 1000] |
| 72 | +Base-10 logarithms: [0. 1. 2. 3.] |
| 73 | +log10(10000) = 4.0 |
| 74 | +Mixed values: [ 100 10 1 0 -10] |
| 75 | +Base-10 logarithms (with warnings): [ 2. 1. 0. -inf nan] |
47 | 76 | ``` |
48 | 77 |
|
49 | | -> **Note:** Running the above code will result in a `RuntimeWarning` due to attempting to calculate the logarithm of a negative number, which is not a valid operation. |
| 78 | +This example shows that `.log10()` returns the expected mathematical results: `log10(1)=0`, `log10(10)=1`, `log10(100)=2`, etc. For zero, it returns negative infinity, and for negative numbers, it returns NaN. |
50 | 79 |
|
51 | | -## Codebyte Example |
| 80 | +## Example 2: Visualizing Logarithmic Data |
52 | 81 |
|
53 | | -In this codebyte example, the `.log10()` method only computes the base-10 logarithm of positive elements in the array: |
| 82 | +This example creates a visual comparison between linear and logarithmic scales, which is useful for datasets that span multiple orders of magnitude: |
54 | 83 |
|
55 | | -```codebyte/python |
| 84 | +```py |
56 | 85 | import numpy as np |
| 86 | +import matplotlib.pyplot as plt |
| 87 | + |
| 88 | +# Generate data with exponential growth |
| 89 | +x = np.linspace(0, 5, 100) |
| 90 | +y = np.power(10, x) # Values will range from 1 to 100,000 |
| 91 | + |
| 92 | +# Create a figure with two subplots |
| 93 | +fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5)) |
| 94 | + |
| 95 | +# Plot on linear scale |
| 96 | +ax1.plot(x, y, 'b-') |
| 97 | +ax1.set_title('Linear Scale') |
| 98 | +ax1.set_xlabel('x') |
| 99 | +ax1.set_ylabel('y = 10^x') |
| 100 | +ax1.grid(True) |
| 101 | + |
| 102 | +# Plot on log scale (equivalent to plotting log10(y) on a linear scale) |
| 103 | +ax2.plot(x, np.log10(y), 'r-') |
| 104 | +ax2.set_title('Logarithmic Scale (base-10)') |
| 105 | +ax2.set_xlabel('x') |
| 106 | +ax2.set_ylabel('log10(y)') |
| 107 | +ax2.grid(True) |
| 108 | + |
| 109 | +plt.tight_layout() |
| 110 | +plt.show() |
| 111 | + |
| 112 | +# Print some values to understand the transformation |
| 113 | +sample_points = [0, 1, 2, 3, 4, 5] |
| 114 | +for point in sample_points: |
| 115 | + value = 10**point |
| 116 | + log_value = np.log10(value) |
| 117 | + print(f"x = {point}, y = {value}, log10(y) = {log_value}") |
| 118 | +``` |
57 | 119 |
|
58 | | -result = np.log10([1, 0.1, 1000], where=np.array([1, 0.1, 1000]) > 0) |
| 120 | +The output of the above code will be: |
59 | 121 |
|
60 | | -print(result) |
| 122 | +```shell |
| 123 | +x = 0, y = 1.0, log10(y) = 0.0 |
| 124 | +x = 1, y = 10.0, log10(y) = 1.0 |
| 125 | +x = 2, y = 100.0, log10(y) = 2.0 |
| 126 | +x = 3, y = 1000.0, log10(y) = 3.0 |
| 127 | +x = 4, y = 10000.0, log10(y) = 4.0 |
| 128 | +x = 5, y = 100000.0, log10(y) = 5.0 |
61 | 129 | ``` |
| 130 | + |
| 131 | +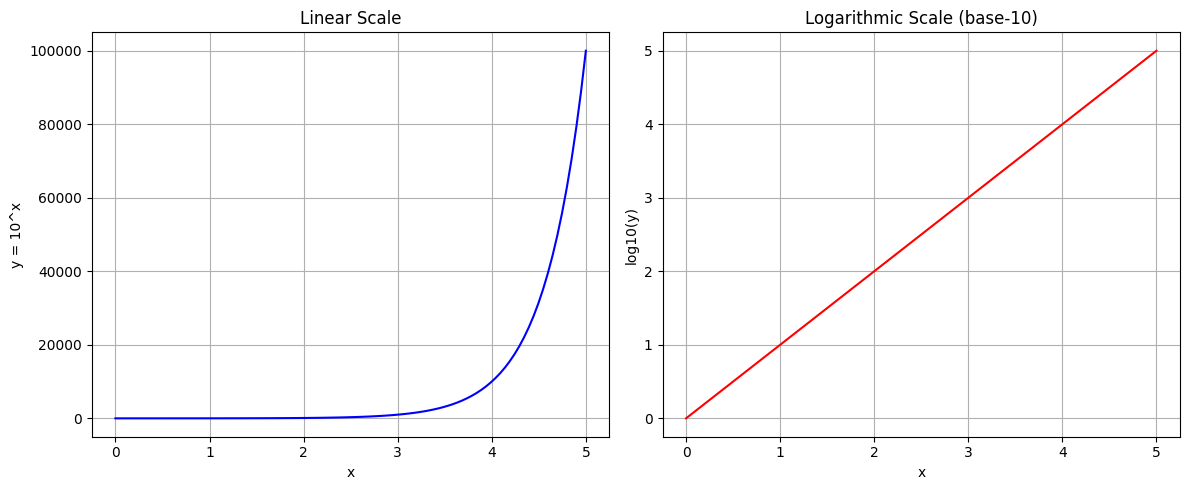 |
| 132 | + |
| 133 | +This example demonstrates how `.log10()` can transform exponentially growing data into a linear relationship, making it easier to visualize and analyze data that spans multiple orders of magnitude. |
| 134 | + |
| 135 | +## Codebyte Example: Analyzing Sound Intensity |
| 136 | + |
| 137 | +This example demonstrates how to use `.log10()` to calculate decibel levels from sound pressure measurements, a common application in audio engineering and acoustics. |
| 138 | + |
| 139 | +```codebyte/python |
| 140 | +import numpy as np |
| 141 | +
|
| 142 | +# Define reference sound pressure level (20 micropascals) |
| 143 | +p_ref = 2e-5 # Pascal |
| 144 | +
|
| 145 | +# Create array of sound pressure measurements (in Pascal) |
| 146 | +# Ranging from reference level to 1000 times reference |
| 147 | +sound_pressures = np.array([p_ref, 2*p_ref, 10*p_ref, 100*p_ref, 1000*p_ref]) |
| 148 | +
|
| 149 | +# Calculate sound pressure level in decibels using the formula: |
| 150 | +# SPL (dB) = 20 * log10(p/p_ref) |
| 151 | +decibels = 20 * np.log10(sound_pressures / p_ref) |
| 152 | +
|
| 153 | +# Display results |
| 154 | +print("Sound Pressure (Pa) | Sound Pressure Level (dB)") |
| 155 | +print("-" * 45) |
| 156 | +for pressure, db in zip(sound_pressures, decibels): |
| 157 | + print(f"{pressure:.8f} Pa | {db:.1f} dB") |
| 158 | +
|
| 159 | +# Examples of common sound levels |
| 160 | +common_sounds = { |
| 161 | + "Threshold of hearing": 0, |
| 162 | + "Whisper": 20, |
| 163 | + "Normal conversation": 60, |
| 164 | + "Heavy traffic": 80, |
| 165 | + "Rock concert": 110, |
| 166 | + "Threshold of pain": 130 |
| 167 | +} |
| 168 | +
|
| 169 | +print("\nCommon Sound Levels:") |
| 170 | +for sound, level in common_sounds.items(): |
| 171 | + # Calculate ratio to reference pressure |
| 172 | + ratio = 10**(level/20) |
| 173 | + pressure = p_ref * ratio |
| 174 | + print(f"{sound}: {level} dB ({pressure:.8f} Pa)") |
| 175 | +``` |
| 176 | + |
| 177 | +This example demonstrates how logarithmic scales are essential for representing sound levels in a way that corresponds to human perception, using `.log10()` to convert between linear pressure measurements and logarithmic decibel values. |
| 178 | + |
| 179 | +## Frequently Asked Questions |
| 180 | + |
| 181 | +### 1. What happens when I use `.log10()` on zero or negative numbers? |
| 182 | + |
| 183 | +For zero values, `.log10()` returns negative infinity (`-inf`). For negative values, it returns NaN (Not a Number) since logarithms of negative numbers are not defined in the real number system. |
| 184 | + |
| 185 | +### 2. How does NumPy's `.log10()` compare to using `np.log(x)/np.log(10)`? |
| 186 | + |
| 187 | +Both approaches calculate the base-10 logarithm, but `.log10()` is optimized for this specific calculation and is typically faster and more numerically stable than the division approach. |
| 188 | + |
| 189 | +### 3. Can I use `.log10()` on complex numbers? |
| 190 | + |
| 191 | +Yes, NumPy's `.log10()` supports complex numbers. For a complex input, it returns the complex base-10 logarithm. |
| 192 | + |
| 193 | +### 4. How do I handle data that includes zeros or negative values when I need to apply a logarithmic transformation? |
| 194 | + |
| 195 | +Common strategies include: |
| 196 | + |
| 197 | +- Adding a small constant to all values: `np.log10(data + epsilon)` |
| 198 | +- Using only positive values: `np.log10(data[data > 0])` |
| 199 | +- Using a symmetric log transformation like `np.sign(data) * np.log10(1 + np.abs(data))` |
| 200 | + |
| 201 | +### 5. Is there a way to specify a different base for logarithms in NumPy? |
| 202 | + |
| 203 | +Yes, you can use the `np.log()` function with the change of base formula: `np.log(x) / np.log(base)`. NumPy also provides specific functions for common bases: `np.log10()` for base-10, `np.log2()` for base-2, and `np.log()` or `np.log1p()` for the natural logarithm. |
0 commit comments