|
| 1 | +## 题目地址(1203. 项目管理) |
| 2 | + |
| 3 | +https://leetcode-cn.com/problems/sort-items-by-groups-respecting-dependencies/ |
| 4 | + |
| 5 | +## 题目描述 |
| 6 | + |
| 7 | +``` |
| 8 | +
|
| 9 | +公司共有 n 个项目和 m 个小组,每个项目要不无人接手,要不就由 m 个小组之一负责。 |
| 10 | +
|
| 11 | +group[i] 表示第 i 个项目所属的小组,如果这个项目目前无人接手,那么 group[i] 就等于 -1。(项目和小组都是从零开始编号的)小组可能存在没有接手任何项目的情况。 |
| 12 | +
|
| 13 | +请你帮忙按要求安排这些项目的进度,并返回排序后的项目列表: |
| 14 | +
|
| 15 | +同一小组的项目,排序后在列表中彼此相邻。 |
| 16 | +项目之间存在一定的依赖关系,我们用一个列表 beforeItems 来表示,其中 beforeItems[i] 表示在进行第 i 个项目前(位于第 i 个项目左侧)应该完成的所有项目。 |
| 17 | +如果存在多个解决方案,只需要返回其中任意一个即可。如果没有合适的解决方案,就请返回一个 空列表 。 |
| 18 | +
|
| 19 | + |
| 20 | +
|
| 21 | +示例 1: |
| 22 | +``` |
| 23 | + |
| 24 | + |
| 25 | + |
| 26 | +``` |
| 27 | +输入:n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]] |
| 28 | +输出:[6,3,4,1,5,2,0,7] |
| 29 | +示例 2: |
| 30 | +
|
| 31 | +输入:n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]] |
| 32 | +输出:[] |
| 33 | +解释:与示例 1 大致相同,但是在排序后的列表中,4 必须放在 6 的前面。 |
| 34 | + |
| 35 | +
|
| 36 | +提示: |
| 37 | +
|
| 38 | +1 <= m <= n <= 3 * 104 |
| 39 | +group.length == beforeItems.length == n |
| 40 | +-1 <= group[i] <= m - 1 |
| 41 | +0 <= beforeItems[i].length <= n - 1 |
| 42 | +0 <= beforeItems[i][j] <= n - 1 |
| 43 | +i != beforeItems[i][j] |
| 44 | +beforeItems[i] 不含重复元素 |
| 45 | +
|
| 46 | +``` |
| 47 | + |
| 48 | +## 前置知识 |
| 49 | + |
| 50 | +- 图论 - 拓扑排序 |
| 51 | +- BFS & DFS |
| 52 | + |
| 53 | +## 公司 |
| 54 | + |
| 55 | +- 暂无 |
| 56 | + |
| 57 | +## 思路 |
| 58 | + |
| 59 | +首先这道题不简单。 题目隐藏了三个考点,参考了其他题解之后,发现他们思路挺不错的,但讲述的并不清楚,于是写下了这篇题解。 |
| 60 | + |
| 61 | +### 考点一 - 如何确定拓扑排序? |
| 62 | + |
| 63 | +对于拓扑排序,我们可以使用 BFS 和 DFS 两种方式来解决。 |
| 64 | + |
| 65 | +使用 BFS 则从入度为 0 的开始(没有任何依赖),将其邻居(依赖)逐步加入队列,并将入度(依赖数目)减去 1,如果减到 0 了,说明没啥依赖了,将其入队处理。这种做法不需要使用 visited 数组,因为环的入度不可能为 0,也就不会入队,自然不会有死循环。 |
| 66 | + |
| 67 | +代码: |
| 68 | + |
| 69 | +```py |
| 70 | + def tp_sort(self, items, indegree, neighbors): |
| 71 | + q = collections.deque([]) |
| 72 | + ans = [] |
| 73 | + for item in items: |
| 74 | + if not indegree[item]: |
| 75 | + q.append(item) |
| 76 | + while q: |
| 77 | + cur = q.popleft() |
| 78 | + ans.append(cur) |
| 79 | + |
| 80 | + for neighbor in neighbors[cur]: |
| 81 | + indegree[neighbor] -= 1 |
| 82 | + if not indegree[neighbor]: |
| 83 | + q.append(neighbor) |
| 84 | + |
| 85 | + return ans |
| 86 | +``` |
| 87 | + |
| 88 | +使用 DFS 可以从图的任意一点出发,基于深度优先遍历检测是否有环。如果有,则返回 [],如果没有,则直接将 path 返回即可。使用此方法需要 visited 数组。 |
| 89 | + |
| 90 | +代码: |
| 91 | + |
| 92 | +```py |
| 93 | +class Solution: |
| 94 | + def tp_sort(self, items: int, pres: List[List[int]]) -> List[int]: |
| 95 | + res = [] |
| 96 | + visited = [0] * items |
| 97 | + adjacent = [[] for _ in range(items)] |
| 98 | + |
| 99 | + def dfs(i): |
| 100 | + if visited[i] == 1: |
| 101 | + return False |
| 102 | + if visited[i] == 2: |
| 103 | + return True |
| 104 | + visited[i] = 1 |
| 105 | + for j in adjacent[i]: |
| 106 | + if not dfs(j): |
| 107 | + return False |
| 108 | + |
| 109 | + visited[i] = 2 |
| 110 | + res.append(i) |
| 111 | + return True |
| 112 | + for cur, pre in pres: |
| 113 | + adjacent[cur].append(pre) |
| 114 | + for i in range(items): |
| 115 | + if not dfs(i): |
| 116 | + return [] |
| 117 | + return res |
| 118 | +``` |
| 119 | + |
| 120 | +相关题目: |
| 121 | + |
| 122 | +- [210. 课程表 II](https://leetcode-cn.com/problems/course-schedule-ii/) |
| 123 | +- [207. 课程表](https://leetcode-cn.com/problems/course-schedule/) |
| 124 | + |
| 125 | +### 考点二 - 如何确定项目的依赖关系? |
| 126 | + |
| 127 | +如下图: |
| 128 | + |
| 129 | +- 圆圈表示的是项目 |
| 130 | +- 黑色线条表示项目的依赖关系 |
| 131 | +- 红色线条表示项目和组之间的依赖关系 |
| 132 | +- 绿色线条是项目之间的依赖关系 |
| 133 | + |
| 134 | +注意绿色线条不是题目给出的,而是需要我们自己生成。 |
| 135 | + |
| 136 | +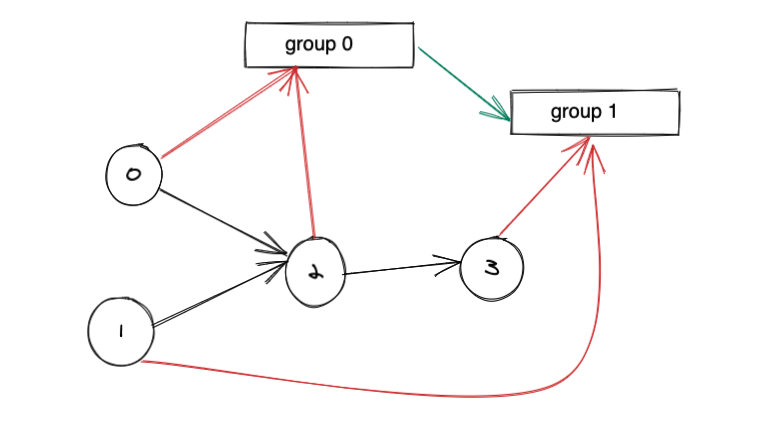 |
| 137 | + |
| 138 | +生成绿色部分依赖关系的核心逻辑是**如果一个项目和这个项目的依赖(如果存在)需要不同的组来完成**,那么这两个组就拥有依赖关系。代码: |
| 139 | + |
| 140 | +```py |
| 141 | + |
| 142 | +for pre in pres[project]: |
| 143 | + if group[pre] != group[project]: |
| 144 | + # 小组关系图 |
| 145 | + group_indegree[group[project]] += 1 |
| 146 | + group_neighbors[group[pre]].append(group[project]) |
| 147 | + else: |
| 148 | + # 项目关系图 |
| 149 | + # ... |
| 150 | +``` |
| 151 | + |
| 152 | +pres 是题目中的 beforeItems,即项目的依赖关系。 |
| 153 | + |
| 154 | +### 考点三 - 无人负责的项目如何处理? |
| 155 | + |
| 156 | +如果无组处理,意味着随便找一个组分配即可,这意味着其是图中入度为零的点。 |
| 157 | + |
| 158 | +一种方法是将这些无人处理的进行编号,只要给分别给它们一个不重复的 id 即可,注意这个 id 一定不能是已经存在的 id。由于原有的 group id 范围是 [0, m-1] 因此我们可以从 m 开始并逐个自增 1 来实现,详见代码。 |
| 159 | + |
| 160 | +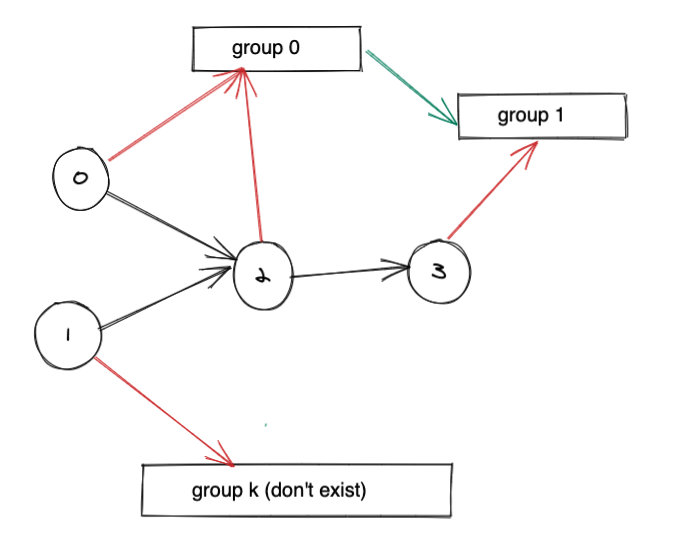 |
| 161 | + |
| 162 | +## 代码 |
| 163 | + |
| 164 | +代码支持:Python3 |
| 165 | + |
| 166 | +Python3: |
| 167 | + |
| 168 | +```py |
| 169 | +class Solution: |
| 170 | + def tp_sort(self, items, indegree, neighbors): |
| 171 | + q = collections.deque([]) |
| 172 | + ans = [] |
| 173 | + for item in items: |
| 174 | + if not indegree[item]: |
| 175 | + q.append(item) |
| 176 | + while q: |
| 177 | + cur = q.popleft() |
| 178 | + ans.append(cur) |
| 179 | + |
| 180 | + for neighbor in neighbors[cur]: |
| 181 | + indegree[neighbor] -= 1 |
| 182 | + if not indegree[neighbor]: |
| 183 | + q.append(neighbor) |
| 184 | + |
| 185 | + return ans |
| 186 | + |
| 187 | + def sortItems(self, n: int, m: int, group: List[int], pres: List[List[int]]) -> List[int]: |
| 188 | + max_group_id = m |
| 189 | + for project in range(n): |
| 190 | + if group[project] == -1: |
| 191 | + group[project] = max_group_id |
| 192 | + max_group_id += 1 |
| 193 | + |
| 194 | + project_indegree = collections.defaultdict(int) |
| 195 | + group_indegree = collections.defaultdict(int) |
| 196 | + project_neighbors = collections.defaultdict(list) |
| 197 | + group_neighbors = collections.defaultdict(list) |
| 198 | + group_projects = collections.defaultdict(list) |
| 199 | + |
| 200 | + for project in range(n): |
| 201 | + group_projects[group[project]].append(project) |
| 202 | + |
| 203 | + for pre in pres[project]: |
| 204 | + if group[pre] != group[project]: |
| 205 | + # 小组关系图 |
| 206 | + group_indegree[group[project]] += 1 |
| 207 | + group_neighbors[group[pre]].append(group[project]) |
| 208 | + else: |
| 209 | + # 项目关系图 |
| 210 | + project_indegree[project] += 1 |
| 211 | + project_neighbors[pre].append(project) |
| 212 | + |
| 213 | + ans = [] |
| 214 | + |
| 215 | + group_queue = self.tp_sort([i for i in range(max_group_id)], group_indegree, group_neighbors) |
| 216 | + |
| 217 | + if len(group_queue) != max_group_id: |
| 218 | + return [] |
| 219 | + |
| 220 | + for group_id in group_queue: |
| 221 | + |
| 222 | + project_queue = self.tp_sort(group_projects[group_id], project_indegree, project_neighbors) |
| 223 | + |
| 224 | + if len(project_queue) != len(group_projects[group_id]): |
| 225 | + return [] |
| 226 | + ans += project_queue |
| 227 | + |
| 228 | + return ans |
| 229 | +``` |
| 230 | + |
| 231 | +**复杂度分析** |
| 232 | + |
| 233 | +令 m 和 n 分别为图的边数和顶点数。 |
| 234 | + |
| 235 | +- 时间复杂度:$O(m + n)$ |
| 236 | +- 空间复杂度:$O(m + n)$ |
| 237 | + |
| 238 | +大家对此有何看法,欢迎给我留言,我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库:https://github.com/azl397985856/leetcode 。 目前已经 37K star 啦。 |
| 239 | +大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。 |
| 240 | + |
0 commit comments