diff --git a/First_Date_with_TensorFlow.ipynb b/First_Date_with_TensorFlow.ipynb
new file mode 100644
index 0000000..38456f3
--- /dev/null
+++ b/First_Date_with_TensorFlow.ipynb
@@ -0,0 +1,964 @@
+{
+ "nbformat": 4,
+ "nbformat_minor": 0,
+ "metadata": {
+ "colab": {
+ "name": "First_Date_with_TensorFlow.ipynb",
+ "version": "0.3.2",
+ "provenance": [],
+ "include_colab_link": true
+ },
+ "kernelspec": {
+ "name": "python3",
+ "display_name": "Python 3"
+ }
+ },
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "view-in-github",
+ "colab_type": "text"
+ },
+ "source": [
+ "[View in Colaboratory](https://colab.research.google.com/github/amartyabhattacharya/Assignment-4/blob/amartyabhattacharya/First_Date_with_TensorFlow.ipynb)"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
\n",
+ "\n",
+ "You know what's important for understanding Deep Learning / Machine Learning?
\n",
+ "Intuition. Period.\n",
+ "\n",
+ "And Intuition comes when you run the code multiple times.\n",
+ "\n",
+ "So, today I can write a couple of defination and say this is this, this is that.
\n",
+ "You Google half of the things up. You find answers which you need to Google further.
\n",
+ "In the process, you probably won't even remember what's the first thing you started out with!\n",
+ "\n",
+ "So?\n",
+ "\n",
+ "Hence on, I will execute cells with code.
\n",
+ "The neurons in your brain will optimize a function to get a hold of what each function is doing.
\n",
+ "**No Theory Just Code.**\n",
+ "\n",
+ "I will at max give a defination that extends for a line. That's it.
\n",
+ "Let's get started!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "**RECOMMENDED!**
\n",
+ "Write the code in the cells using the signals sent by your brain to your fingers!
\n",
+ "Don't just `shift+enter` the cells.\n",
+ "\n",
+ "[Source](https://github.com/iArunava/TensorFlow-NoteBooks)"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "gYWUpE-bYKWP",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Essential imports\n",
+ "import numpy as np\n",
+ "import tensorflow as tf\n",
+ "import matplotlib.pyplot as plt"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "eKpz5NCIYMdi",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define some tensors\n",
+ "t1 = tf.constant(2.0, dtype=tf.float32)\n",
+ "t2 = tf.constant([1.0, 2.0], dtype=tf.float32)\n",
+ "t3 = tf.constant([[[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]], \n",
+ " [[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]]])"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "vmMcjzTxbWzw",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 71
+ },
+ "outputId": "1c18425d-03fa-43c7-b09b-fe657675d43c"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's print them out!\n",
+ "print (t1)\n",
+ "print (t2)\n",
+ "print (t3)"
+ ],
+ "execution_count": 3,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Tensor(\"Const:0\", shape=(), dtype=float32)\n",
+ "Tensor(\"Const_1:0\", shape=(2,), dtype=float32)\n",
+ "Tensor(\"Const_2:0\", shape=(2, 3, 2), dtype=float32)\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "10ahnfjYbcop",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Where's Waldo?
\n",
+ "I mean, the value?
\n",
+ "\n",
+ "So, the thing is you can't print the value of tensors directly.
\n",
+ "You have to use `session`, so let's do that!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "ol6O5I7Tb2nb",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 215
+ },
+ "outputId": "63a2fb5d-e947-40ca-ed68-356c39fb8ce9"
+ },
+ "cell_type": "code",
+ "source": [
+ "sess = tf.Session()\n",
+ "print (sess.run(t1))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t2))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t3))\n",
+ "sess.close()"
+ ],
+ "execution_count": 4,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "2.0\n",
+ "=======================\n",
+ "[1. 2.]\n",
+ "=======================\n",
+ "[[[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]\n",
+ "\n",
+ " [[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "rXKfVs_zb-kU",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Aaahaa!! Just printed those tensors!!!
\n",
+ "Feels good!
\n",
+ "\n",
+ "For some of you, who are like, dude you got \"No Theory Just Code\" in bold
\n",
+ "And you are still using the markdown cells for the theory ?!\n",
+ "\n",
+ "I am just gonna say I am a unreasonable man.
\n",
+ "\n",
+ "\n",
+ "So, you are programming with tf.
\n",
+ "What ever you do is broken down to 2 basic steps:\n",
+ "- Building the computational Graph!\n",
+ "- Execute that graph using `session`!\n",
+ "\n",
+ "That's all!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Let's compare this 2 steps with what we did above!
\n",
+ "So, I defined 3 `tensor`s and these 3 `tensor`s formed my computational Graph.
\n",
+ "And then I executed each tensor in this graph using a `session`.\n",
+ "\n",
+ "That simple!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Now, let's define a few more computational graphs and execute them with sessions.\n",
+ "\n",
+ "Okay, to start with let's build this computational graph!\n",
+ "\n",
+ "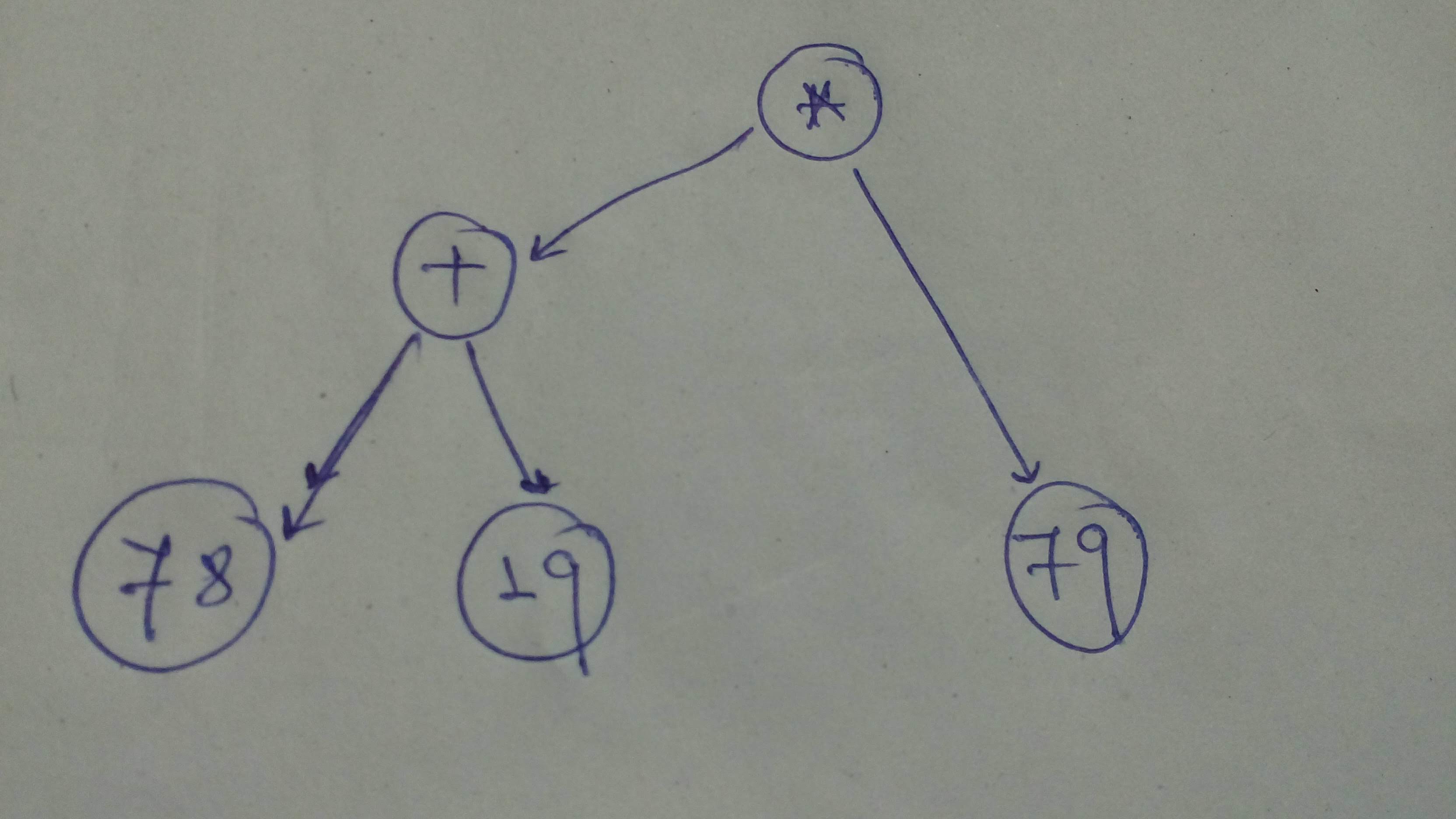"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "FyVz0GNqgreZ",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 53
+ },
+ "outputId": "ece3c1ae-6ab3-4b21-e095-ba67227af0e5"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the graph\n",
+ "comp_graph_1 = tf.multiply(tf.add(78, 19), 79)\n",
+ "\n",
+ "# Alternatively\n",
+ "comp_graph_1_alt = (tf.constant(78) + tf.constant(19)) * tf.constant(79)\n",
+ "\n",
+ "# Let's execute using session\n",
+ "sess = tf.Session()\n",
+ "print ('Comp Graph 1 : ', sess.run(comp_graph_1))\n",
+ "print ('Comp Graph 1 Alt: ', sess.run(comp_graph_1_alt))\n",
+ "sess.close()"
+ ],
+ "execution_count": 5,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Comp Graph 1 : 7663\n",
+ "Comp Graph 1 Alt: 7663\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "SVMMtuFYhaQB",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's define a sligtly more involved graph!\n",
+ "\n",
+ "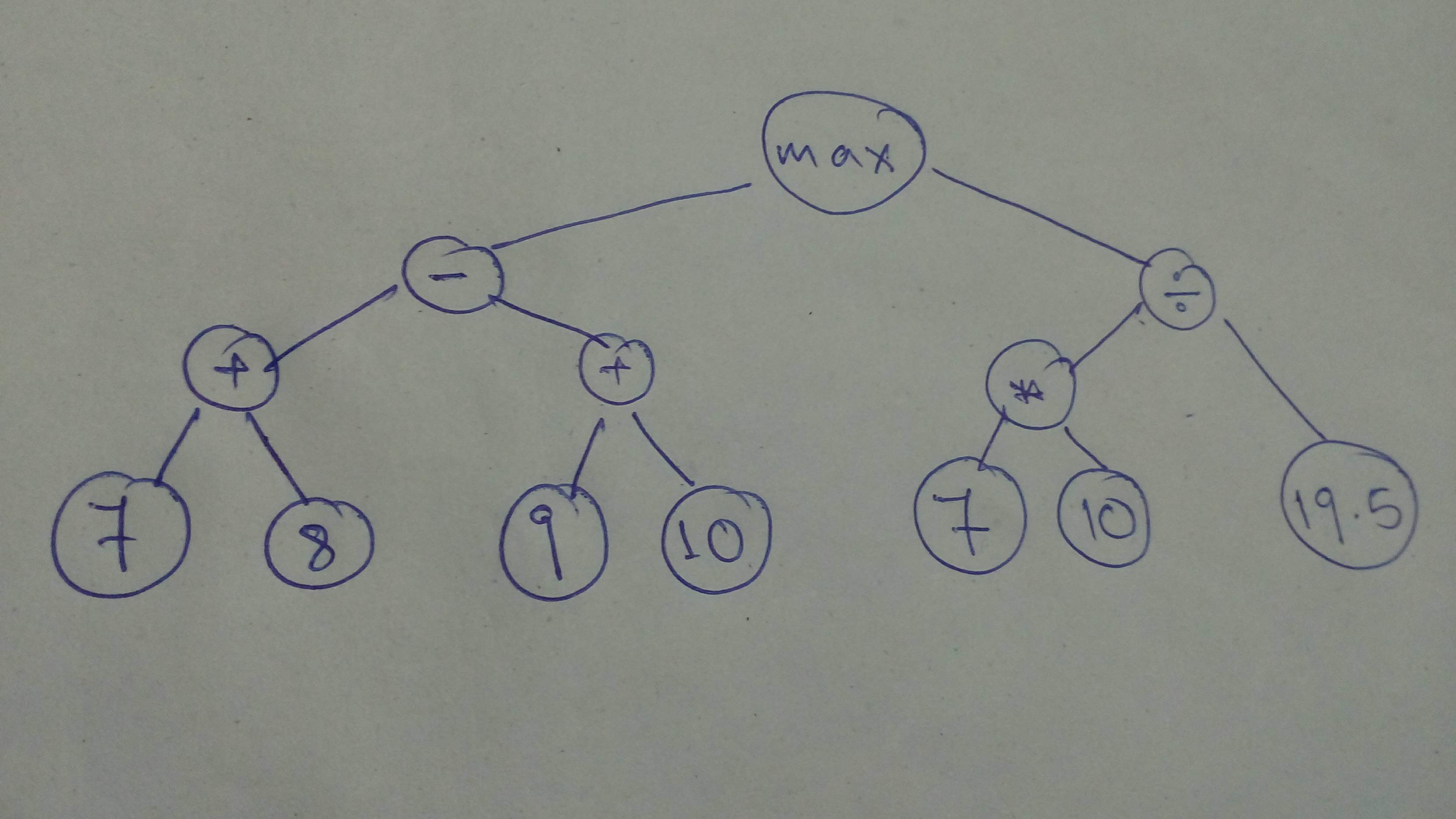"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "4856BTvRhiBb",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 71
+ },
+ "outputId": "3aae115b-74d9-4514-8a09-d3bff7be18b3"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let build the graph\n",
+ "# We need to cast cause the tensors operated on should be of the same type\n",
+ "comp_graph_part_1 = tf.cast(tf.subtract(tf.add(7, 8), tf.add(9, 10)), \n",
+ " dtype=tf.float32)\n",
+ "comp_graph_part_2 = tf.divide(tf.cast(tf.multiply(7, 10), dtype=tf.float32), tf.constant(19.5))\n",
+ "comp_graph_complete = tf.maximum(comp_graph_part_1, comp_graph_part_2)\n",
+ "\n",
+ "# Let's execute\n",
+ "sess = tf.Session()\n",
+ "part1_res, part2_res, total_res = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n",
+ "print ('Complete Result: ', total_res)\n",
+ "print ('Part 1 Result: ', part1_res)\n",
+ "print ('Part 2 Result: ', part2_res)\n",
+ "sess.close()"
+ ],
+ "execution_count": 6,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: 3.5897436\n",
+ "Part 1 Result: -4.0\n",
+ "Part 2 Result: 3.5897436\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "B-_ZDtEbj4N0",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Cool! Let's go! Build another graph and execute it with sessions.
\n",
+ "\n",
+ "But this time, it's all you!\n",
+ "\n",
+ "Build this graph and execute it with `session`!\n",
+ "\n",
+ "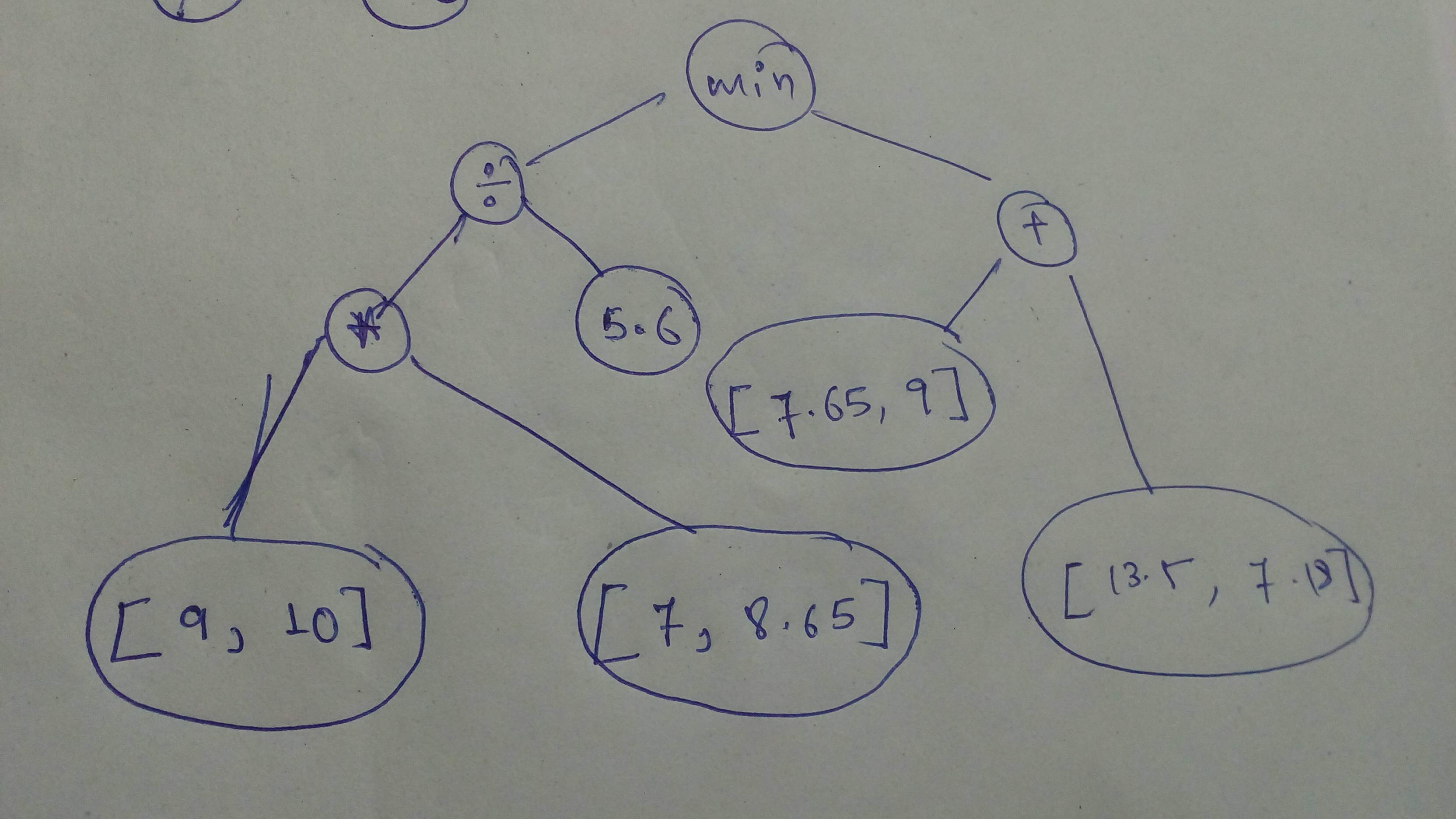\n",
+ "\n",
+ "_Remember that `tensors` operated on should be of the same type!_
\n",
+ "_Search up errors and other help you need on Google_"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "-uHNe1BolJY0",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 35
+ },
+ "outputId": "3686b947-f8cf-47f5-fd7a-d8b37c4c76d7"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "cg1 = tf.divide((tf.constant([9, 10], dtype = tf.float32) * tf.constant([7, 8.65], dtype = tf.float32)) , tf.constant(5.6, dtype = tf.float32))\n",
+ "cg2 = tf.constant([7.65, 9], dtype = tf.float32) + tf.constant([13.5, 7.18], dtype = tf.float32)\n",
+ "cg = tf.maximum(cg1, cg2)\n",
+ " \n",
+ "\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "with tf.Session() as sess:\n",
+ " print(sess.run(cg))"
+ ],
+ "execution_count": 7,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "[21.15 16.18]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "qmap38WelREN",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's do another!
\n",
+ "It's fun! Isn't it?!\n",
+ "\n",
+ "Build and execute this one!\n",
+ "\n",
+ "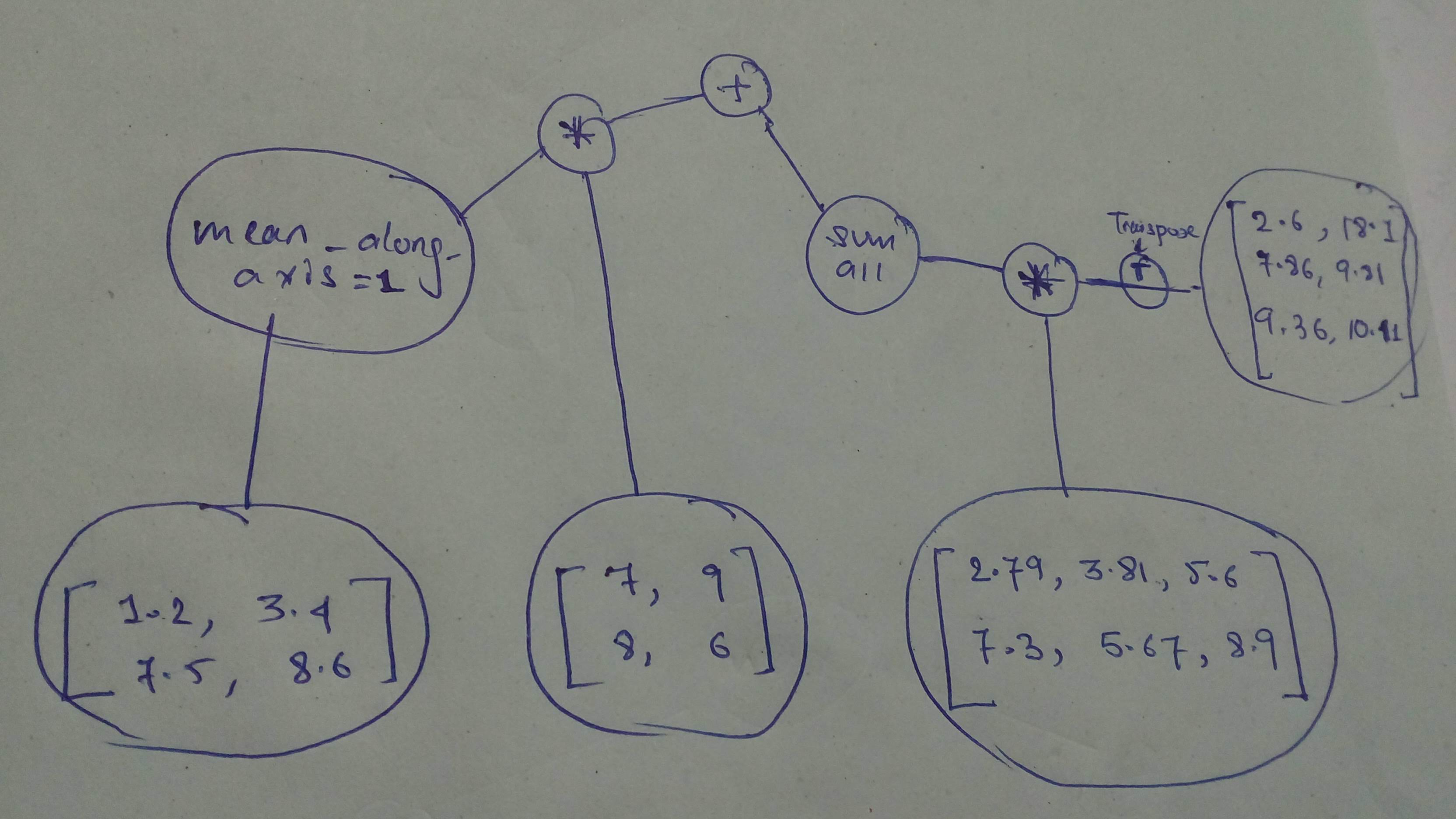"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "0ZhYwAlLmEvB",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 53
+ },
+ "outputId": "3d1ed3a4-4164-4efc-abad-c2482d614ed3"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "node1 = tf.constant([[1.2, 3.4], [7.5, 8.6]],dtype = tf.float32)\n",
+ "node2 = tf.constant([[7, 9], [8, 6]],dtype = tf.float32)\n",
+ "node3 = tf.constant([[2.79, 3.81, 5.6], [7.3, 5.67, 8.9]],dtype = tf.float32)\n",
+ "node4 = tf.constant([[2.6, 18.1], [7.86, 9.81], [9.36, 10.11]],dtype = tf.float32)\n",
+ "\n",
+ "cg1 = tf.reduce_mean(node1, axis = 1) * node2\n",
+ "cg2 = tf.reduce_sum(node3 * tf.transpose(node4))\n",
+ "\n",
+ "cg = cg1 + cg2\n",
+ "\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "with tf.Session() as sess:\n",
+ "# print(sess.run(cg1))\n",
+ "# print(sess.run(cg2))\n",
+ " print(sess.run(cg))"
+ ],
+ "execution_count": 8,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "[[383.4483 439.7983 ]\n",
+ " [385.7483 415.64832]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "BnB0b6qCmGmg",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "And a final one, before we move on to the next part!\n",
+ "\n",
+ "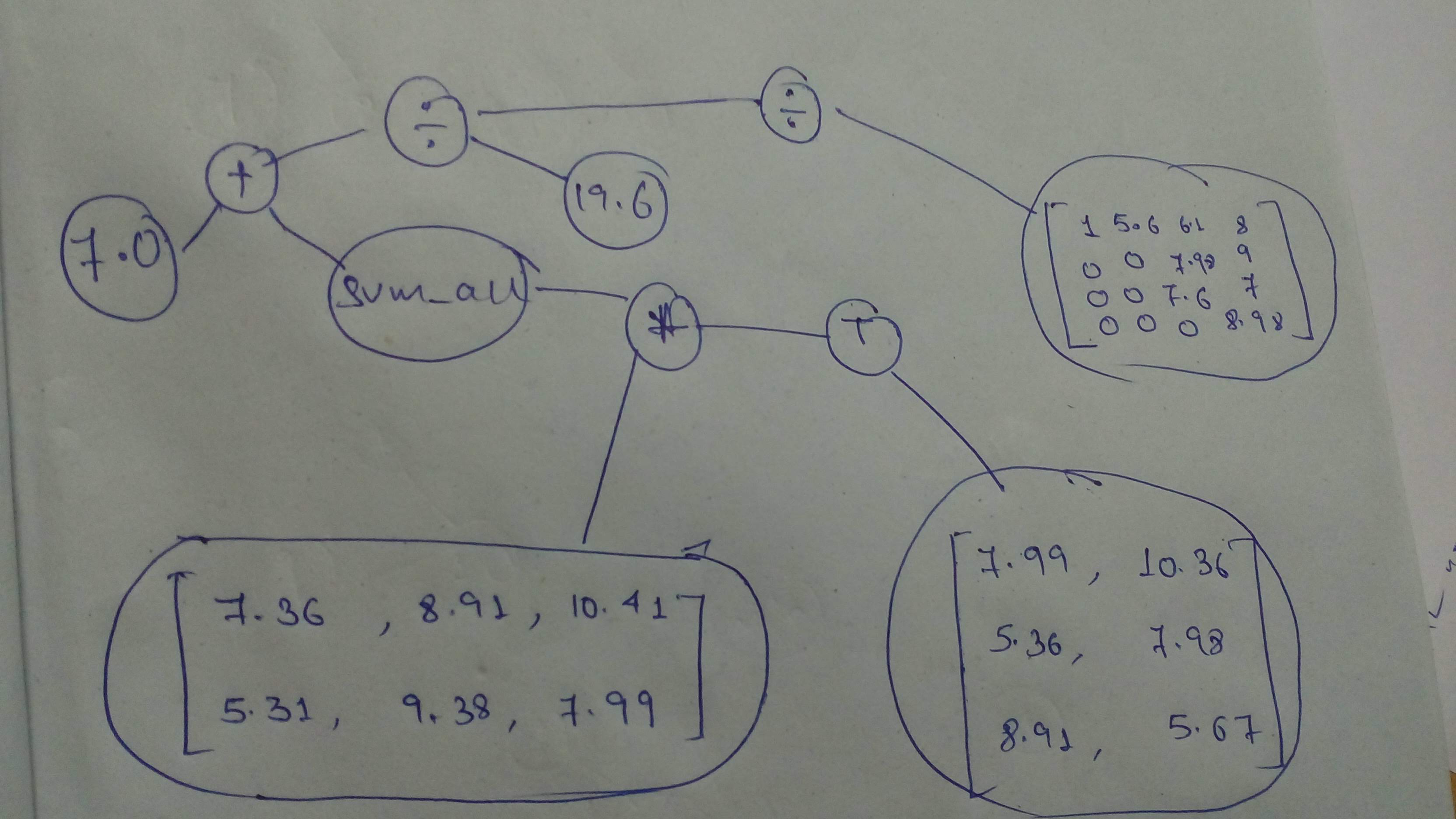"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "GQWyCvsQmMcL",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 89
+ },
+ "outputId": "db0ed2eb-a306-4454-aacd-3dd3557c21e8"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "node1 = tf.constant(7.0, dtype = tf.float32)\n",
+ "node2 = tf.constant([[7.36, 8.91, 10.41], [5.31, 9.38, 7.99]], dtype = tf.float32)\n",
+ "node3 = tf.constant([[7.99, 10.36], [5.36, 7.98], [8.91, 5.67]], dtype = tf.float32)\n",
+ "node4 = tf.constant([[1, 5.6, 6.1, 8], [0, 0, 7.98, 9], [0, 0, 7.6, 7], [0, 0, 0, 8.98]], dtype = tf.float32)\n",
+ "\n",
+ "cg1 = (node1 + tf.reduce_sum(node2 * tf.transpose(node3))) / 19.6\n",
+ "\n",
+ "cg = cg1 / node4\n",
+ "\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "with tf.Session() as sess:\n",
+ " print(sess.run(cg))"
+ ],
+ "execution_count": 9,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "[[19.463488 3.475623 3.1907358 2.432936 ]\n",
+ " [ inf inf 2.4390335 2.1626098]\n",
+ " [ inf inf 2.5609853 2.7804983]\n",
+ " [ inf inf inf 2.1674263]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "12NC7XTPsJw7",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# Linear Regression\n",
+ "\n",
+ "Okay, now we will create a dummy dataset and perform linear regression on this dataset!\n",
+ "\n",
+ "\n",
+ "To get you in the habit of looking up for the documentation, I am not providing what some of the following functions does, Google them up!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "hW31RZkjtNwI",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Create the dataset\n",
+ "X = np.linspace(-30.0, 300.0, 300)\n",
+ "Y = 2 * np.linspace(-30.0, 250.0, 300) + np.random.randn(*X.shape)\n",
+ "\n",
+ "# Normalize the dataset\n",
+ "X = X / np.max(X)\n",
+ "Y = Y / np.max(Y)\n",
+ "\n",
+ "# Divide it into train and test\n",
+ "train_X = X[:250]\n",
+ "train_Y = Y[:250]\n",
+ "\n",
+ "test_X = X[250:]\n",
+ "test_Y = Y[250:]"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "LQKy6U33y4lt",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the hyperparameters\n",
+ "learning_rate = 0.00001\n",
+ "n_epochs = 60\n",
+ "interval = 20"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "1h1-D8K1uT48",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 347
+ },
+ "outputId": "2b7756a5-86b5-41d3-91bf-6cc984e1d1ab"
+ },
+ "cell_type": "code",
+ "source": [
+ "# let's viz the first 10 datapoints of the dataset\n",
+ "plt.plot(train_X[:10], train_Y[:10], 'g')\n",
+ "plt.show()"
+ ],
+ "execution_count": 12,
+ "outputs": [
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAfIAAAFKCAYAAADmCN3IAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzt3XlcVQX+xvEPi8giICig5oqhVIob\naumoaeG+ZWIypUMxbZrW6MxIVJozmjRFmaM1maZmpolbioaWkWWSG0VmuaSZJoqgIAIqCOf3RyO/\nGPfrhcO993m/Xr3q3nvOuc+3mz2ccy7nOBmGYSAiIiI2ydnsACIiImI5FbmIiIgNU5GLiIjYMBW5\niIiIDVORi4iI2DAVuYiIiA1zNTuAJbKyzlh9m35+nuTkFFp9u1WZZnYMjjgzOObcmtm+BQR4X/Z5\n7ZH/l6uri9kRKp1mdgyOODM45tya2TGpyEVERGyYilxERMSGqchFRERsmIpcRETEhqnIRUREbJiK\nXERExIZZ9HvkxcXFxMbGkpGRgYuLC9OmTaNBgwblllm9ejULFizA2dmZYcOGERkZSWZmJnFxcRQV\nFVFaWsqzzz5LixYt6NGjB3Xq1MHF5bdfI3j11VcJCgq6+elERETsnEVFnpSUhI+PDwkJCWzevJmE\nhASmT59e9nphYSGzZs1i2bJlVKtWjaFDhxIREcH8+fOJiIhg+PDhpKWl8frrrzN37lwA3nnnHby8\nvKwzlYiIiIOw6NB6amoqERERAHTq1Im0tLRyr6enp9OyZUu8vb1xd3enbdu2pKWl4efnR25uLgB5\neXn4+fndZHwRERHHZtEeeXZ2Nv7+/gA4Ozvj5OREUVERbm5ul7wO4O/vT1ZWFtHR0QwdOpRVq1aR\nn5/P4sWLy5aZNGkSR48epV27dowfPx4nJ6crvr+fn2eFXM3nSpe/s2ea2TE44szgmHNrZsdzzSJP\nTEwkMTGx3HPp6enlHhuGcdVtXHx9zpw59OnThyeffJKUlBRefvllZs6cydixY+nSpQu+vr6MHj2a\n9evX07t37yturyKuqxsQ4F0h13CvyjSzY3DEmcEx59bMVUP22WxSDn/KoFuH4ObiZrXtWnyt9cjI\nSJYuXVrur/vuu4+srCzgty++GYZRtjcOEBgYSHZ2dtnjEydOEBgYSFpaGl26dAGgc+fOfP/99wAM\nHjyYWrVq4erqSteuXdm3b5/lk4qIiJhkV1Y6PRO7MXrjY/x4cnelvKdF58g7d+5McnIyACkpKXTs\n2LHc661atWLXrl3k5eVRUFBAWloa4eHhNGrUqGxv/rvvvqNRo0acOXOGmJgYioqKANi+fTshISE3\nM5OIiEilW7V/Of1X9uTX/CNM6PAcYQGtK+V9LTpH3rdvX7Zs2UJUVBRubm7Ex8cDMHv2bNq3b0+b\nNm0YP348MTExODk5MXr0aLy9vXn88cd57rnnyn4IeO655/D29qZr16488MADVK9endtvv/2qh9VF\nRESqklKjlPitU5ie9ipe1WqwoM9i+jTpV2nv72Rc6wR3FVQR50Oq4nmWiqaZHYMjzgyOObdmrnxn\nivIY9emjrD/0MY19mvBe3yWE+t9WIe91pXPkFu2Ri4iIOLqDuT8x8uMo9uXspWv97rzTcx5+7v7X\nXtHKdIlWERGRG/TZ4U/ptbwH+3L28njYKJb0X25KiYP2yEVERK6bYRi8lT6Tf6S+gKuTKzN6vMXw\n0AdNzaQiFxERuQ7nLpxj/OdjSdy3hCDPOszvs4h2Qe3NjqUiFxERuZZj+RlEJ/+Rb06k0TawHfP7\nfEAdr7pmxwJU5CIiIle14/g2opMf5ERhJsOaR/Fqtzdwd3U3O1YZFbmIiMgVLP7xff626RkuGBf4\nZ+dpPBY26qr3AjGDilxEROR/XCi9wItbnmP2d29Rs3pNZvecz90Nepgd67JU5CIiIr9z6txJHt3w\nMF/++jnN/UJZ0Hcxwb5NzY51RSpyERGR//rx5A+M/Hg4v+Qdonfjvsy6dzbebj5mx7oqXRBGREQE\nWHcwib4r7uWXvEOMC/878/t8UOVLHLRHLiIiDq7UKOW1Hf/iX9tfwtPVkzk9FzDw1vvMjnXdVOQi\nIuKw8ovzGbvxSZIOfkQD74bM7/MBLWuHmR3rhqjIRUTEIf2Sd4iR66L48dRuOtX7A3N6vUdtj9pm\nx7phOkcuIiIOZ/PRL+i17G5+PLWbh1v8mcQBH9lkiYP2yEVExIEYhsG738/m+c2xODs582q3Nxh5\nx8Nmx7opKnIREXEI50vO8+wXf+X9HxdQ26M27/ZexJ117zI71k1TkYuIiN07UXiCh5MfZPvxrYQF\ntGZ+70XU925gdiyrUJGLiIhd+/ZEGtEfP0hGwVHuu/V+Xu8+C89qnmbHshoVuYiI2K3l+5byl5Sn\nOF9ynufvnMyYNs9UuZue3CwVuYiI2J2S0hKmbp3MzG+m4+3mw9xe7xHRuLfZsSqEilxEROzK6fO5\nPPFJDBsPf0LTmrfyXp8lhPg1MztWhVGRi4iI3fgpZz8jPn6AA7k/0aPhvbwd8S6+1WuaHatC6YIw\nIiJiFz79ZT29lnfnQO5PjG79NIv6Jtp9iYP2yEVExMYZhsG/v5nO1K9fpLpLdd689x2GNnvA7FiV\nRkUuIiI2q7C4kCc/jWHF/mXU9arHgj4f0DqwrdmxKpWKXEREbNLRM78Ss/Ih0o6l0b5OR97t/T5B\nnkFmx6p0KnIREbE5W499zcPJD5J9NosHbxtJfNcEqrtUNzuWKVTkIiJiUxb+MJ/YL8ZTapTy7z7/\nZljjkXZ3kZcboSIXERGbUFxSzAtfxfLu9+/g7+7PnF7vcV/rfmRlnTE7mqlU5CIiUuWdPHuSP68f\nyVcZX3Kb/x2813cxjXwamx2rSrCoyIuLi4mNjSUjIwMXFxemTZtGgwbl7yKzevVqFixYgLOzM8OG\nDSMyMpLCwkJiY2PJzs7Gw8OD+Ph4AgIC2LNnDy+++CIAzZs3Z/LkyTc9mIiI2Ifvs3cR/fEfOXzm\nF/oFD+Tf9/yHGtVqmB2ryrDogjBJSUn4+PiwePFinnjiCRISEsq9XlhYyKxZs5g/fz4LFy5kwYIF\n5ObmsnTpUho0aMAHH3zAk08+yYwZMwCYOnUqcXFxLFmyhPz8fDZt2nTzk4mIiE0zDIOlexfTf0UE\nh8/8wt/bxzG313sq8f9hUZGnpqYSEREBQKdOnUhLSyv3enp6Oi1btsTb2xt3d3fatm1LWloahw4d\nIiwsDIDw8HB27txJUVERR48eLXu+e/fupKam3sxMIiJi47LPZvPI+hE8tfFxnJycmdd7EX9tH4uz\nky5I+r8s+jeSnZ2Nv7//bxtwdsbJyYmioqLLvg7g7+9PVlYWzZo1K9vb3rZtGxkZGeTk5ODj41O2\nbK1atcjKyrJoGBERsX3JP6+j65KOrD24mrvqdebzB7bQL3iA2bGqrGueI09MTCQxMbHcc+np6eUe\nG4Zx1W1cfH3o0KHs3buXqKgoOnToUK7sr3dbAH5+nri6ulxzuRsVEOBt9W1WdZrZMTjizOCYc9vy\nzKfPneaZ9c8w/9v5VHepTkLPBJ6585lr7oXb8szWcM0ij4yMJDIystxzsbGxZGVlERoaSnFxMYZh\n4ObmVvZ6YGAg2dnZZY9PnDhB69atcXNzK/siW0FBARs3bsTf35/c3NyyZTMzMwkMDLxqppycwuub\n7gYEBHg73K8waGbH4Igzg2PObcszbz76BWM3Psmv+UcIC2jNzHveJtT/Nk5mF1x1PVue+UZd6QcW\niw6td+7cmeTkZABSUlLo2LFjuddbtWrFrl27yMvLo6CggLS0NMLDw9m0aRPTp08HfvtWe5cuXahW\nrRrBwcHs2LEDgA0bNtClSxdLYomIiI05e+EsL2yOZchH/TlWkMH48Al8PGQjof63mR3NZlj062d9\n+/Zly5YtREVF4ebmRnx8PACzZ8+mffv2tGnThvHjxxMTE4OTkxOjR4/G29ubjh07smjRIoYNG4av\nry+vvfYaAHFxcUycOJHS0lJatWpFp06drDehiIhUSd9k7uSpjY+zP3cft9YMYdY9s2kT1M7sWDbH\nybiek9JVTEUcRnGkwzMXaWbH4Igzg2PObSszF5cU8/rOV3h95yuUGCU8FvYkz935Ih6uHje8LVuZ\n2RqudGhdV3YTEZFKs/fUHp7a+DjpWd9Qv0YD3ujxJl3qdzM7lk1TkYuISIUrNUp5O/1NXto6mfMl\n5xke+iBTOsfjU93X7Gg2T0UuIiIV6nDeL4z97Em2ZGymtkdtZt89nz5N+pkdy26oyEVEpEIYhsEH\nPy7k+a9iKSjOp2+TAbzSbToBngFmR7MrKnIREbG6zMJMxqeMYcMvyXi7+TDznreJbDbcoe8bXlFU\n5CIiYlVrDqzib5ue4dS5U3Spfzczur/JLd71zY5lt1TkIiJiFbnncnj2y7+xfP9SPFw9mNblFR5u\n8ahudFLBVOQiInLTUg5v5JmU0RwryKBdUDgz73mbpjVDzI7lEFTkIiJisYLiAiZveZ75u+fi6uzK\nsx1eYEzbv+DqrHqpLPo3LSIiFtl2bCtjPnucn08fJNT/NmbdM5uWAa3MjuVwVOQiInJDzpec59Xt\n8fz7m9cxDIPRrZ9mQofncHd1NzuaQ1KRi4jIddud/T2jNz7GDye/p6FPY2b2+A931tONrsykIhcR\nkWsqKS1h1rdv8PK2qRSXFjPi9oeZ3GkKNdwufyMPqTwqchERuaqDpw8wZuMTbD++lSDPOrze/d/c\n26iX2bHkv1TkIiJyWYZhMH/3XCZveZ7CC4UMvnUI8V0T8HevZXY0+R0VuYiIXOJYfgbPpIwm5chG\nalavyevdZ3JfyFCzY8llqMhFRKSMYRis2J9I7Jd/5fT5XHo0vJfp3WdRx6uu2dHkClTkIiICwMmz\nJ5nwxThWH1iJp6sXr3SbzsjbH9aNTqo4FbmIiPDJoWT+8vkYThRm0rHuXczo8RZNfIPNjiXXQUUu\nIuLAzhTlMfGrOBb9+B5uzm5MvOufPNnqKVycXcyOJtdJRS4i4qC2HN3M2M+e5PCZX2hRO4yZ97zN\n7bXuMDuW3CAVuYiIgzl34Rwvbf0Hb6fPwsnJib+0+yvjw2Nxc3EzO5pYQEUuIuJA0k98w1MbH2dv\nzh6CfZsy8563Ca/TwexYchNU5CIiDmLurtm88FUsF0ovENPyMZ6/czJe1bzMjiU3SUUuIuIA/pM+\nk4lfxRHoGcTMe97m7gY9zI4kVqIiFxGxc299O5NJW+Ko41WXlYOSaFozxOxIYkXOZgcQEZGKM+ub\nGUzaEkddr3qsGrRWJW6HVOQiInbq399MZ3Lq89TzuoWVg9cSXPNWsyNJBdChdREROzQj7XWmfD2J\nW2rUZ8WgJF2lzY6pyEVE7MwbOxOYunUyt9Soz8pBa2ns28TsSFKBVOQiInbk9R2vMG3bP6lfowEr\nBiWpxB2AilxExE5M+WIK07b9kwbeDVkxKIlGPo3NjiSVwKIiLy4uJjY2loyMDFxcXJg2bRoNGjQo\nt8zq1atZsGABzs7ODBs2jMjISAoLC4mNjSU7OxsPDw/i4+MJCAhgxIgRFBYW4unpCcCECRNo0aLF\nzU8nIuIgXt0ez7+2v0RD70asGJREQ59GZkeSSmJRkSclJeHj40NCQgKbN28mISGB6dOnl71eWFjI\nrFmzWLZsGdWqVWPo0KFERESwatUqGjRowIwZM9ixYwczZszgn//8JwDTpk2jWbNm1plKRMSB/Gvb\nS7y6I54mNZuwbMAaGng3NDuSVCKLfv0sNTWViIgIADp16kRaWlq519PT02nZsiXe3t64u7vTtm1b\n0tLSOHToEGFhYQCEh4ezc+fOm4wvIuK4DMPg5W1TeXVHPA19GvN59OcqcQdkUZFnZ2fj7+//2wac\nnXFycqKoqOiyrwP4+/uTlZVFs2bN2LRpEwDbtm0jIyOjbJkZM2bw4IMPMnHiRM6dO2fRMCIijsIw\nDF7ePpWEHS/TyKcxHw1aR0Nflbgjuuah9cTERBITE8s9l56eXu6xYRhX3cbF14cOHcrevXuJioqi\nQ4cOZWU/cuRImjdvTsOGDZk0aRKLFi0iJibmitvz8/PE1dX6N70PCPC2+jarOs3sGBxxZrDfuQ3D\n4IWUF3htx79o6teUz6M/p75PfcB+Z74aR5z5965Z5JGRkURGRpZ7LjY2lqysLEJDQykuLsYwDNzc\n/v8+toGBgWRnZ5c9PnHiBK1bt8bNzY3JkycDUFBQwMaNGwHKDtMD9OjRg3Xr1l01U05O4XWMdmMC\nArzJyjpj9e1WZZrZMTjizGC/cxuGwUtb/8EbaQk08Q1m+YAkqp/3JSvrjN3OfDWONPOVfmCx6NB6\n586dSU5OBiAlJYWOHTuWe71Vq1bs2rWLvLw8CgoKSEtLIzw8nE2bNpV9KW716tV06dIFwzCIjo4m\nLy8PgK1btxISomsBi4j8L8MwmPr1ZN5ISyDYtymrBq2jXo1bzI4lJrPoW+t9+/Zly5YtREVF4ebm\nRnx8PACzZ8+mffv2tGnThvHjxxMTE4OTkxOjR4/G29ubjh07smjRIoYNG4avry+vvfYaTk5ODBs2\njOjoaDw8PAgKCmLMmDFWHVJExNYZhsE/v57EzG+m07TmrawctJY6XnXNjiVVgJNxrRPcVVBFHEZx\npMMzF2lmx+CIM4N9zW0YBpNTX+DNb2dwa80QVgxKumyJ29PM18uRZr7SoXVd2U1EpAozDIMXtzzP\nW+n/JqRmM1YMSiLIq47ZsaQKUZGLiFRRhmEwcUscb6fPoplfc5YPSiLIM8jsWFLFqMhFRKogwzB4\n4atYZn/3Fs39Qlk+KIlAz0CzY0kVpCIXEaliDMPg+c0TeGfXfwj1v41lA9eoxOWKVOQiIlWIYRjE\nbf4bc3fN5jb/21k2cA0BngFmx5IqTEUuIlJFGIZB7Jfjmff9HG7zv4Plg9ZQ26O22bGkirPogjAi\nImJdpUYpE74Yx7zv53B7rRYqcblu2iMXETHZbyU+ngW753JHrZYsG7iaWh61zI4lNkJFLiJiolKj\nlL9t+gsLf5hHi9phLBv4Ef7uKnG5fipyERGTlBql/PXzp3n/xwW0rN2KxIGrVOJyw1TkIiImKDVK\nGf/5WBb9+B5hAa1JHLAKP3d/s2OJDVKRi4hUslKjlL+kPMXiPe/TKqANiQNWUdPdz+xYYqNU5CIi\nlaiktIS/fP4US/YsonVAGxIHfoRv9ZpmxxIbpiIXEakkJaUlPJ0yiqV7F9MmsC1LB6xSictNU5GL\niFSCktISxn72JIn7ltAuKJwP+6/Ep7qv2bHEDqjIRUQqWElpCU9tfJzl+5fSLqg9H/ZfoRIXq1GR\ni4hUoAulF3hq4+Os2J9IeFAHPhywAm83H7NjiR3RJVpFRCrIbyX+GCv2J9K+TkeVuFQI7ZGLiFSA\nC6UXGPXpn1n10wo61LmTJf2XU8PN2+xYYodU5CIiVlZcUsyTn/6Z1QdW0rHuXSzut0wlLhVGRS4i\nYkXFJcU88WkMaw6s4s66nfig/zJqVKthdiyxYzpHLiJiJcUlxTz+ySOsObCKTvX+oBKXSqE9chER\nKygqKeKxDQ+z7uc1dK7Xhff7LcWrmpfZscQBqMhFRG5SUUkRj26I5uOfk/jDLV1Z2PdDlbhUGhW5\niMhNKCop4s8b/kTyz2vpcks3Fvb9EM9qnmbHEgeic+QiIhY6X3KemPUjSP55LV3rd1eJiym0Ry4i\nYoHzJeeJSR7Bhl+S6Va/O+/1XYKHq4fZscQBqchFRP7HuQvnOF5wrOyvY2X/nPG7fz7GuZJz3N2g\nBwv6LFaJi2lU5CLiMEpKS8g+l83x/Ixy5Xy84DjH/vv34wUZ5JzPueI2nHAiwDOQZv6htAsKZ3Kn\nl3B3da/EKUTKU5GLiM0zDIMzRXm/K+RjnNlzip9O/FxWzscLjpNZeJwSo+SK2/F286GuV11aBLSi\nrldd6njWpW6NutTxqkcdrzrU9apHgEcg1VyqVeJ0IlenIheRKq2opOi/e84XC/lYucPbF/ekCy8U\nXHEb1ZyrUcerLm2DwqnjVZe6XnUJ+u/ff/9YF28RW6QiFxHTHTlzmJTDGy85L51ZeIzss9lXXbe2\nR22CazYtK+WLf4XWa4r7BV/qetXD390fZyf9ko7YJ4uKvLi4mNjYWDIyMnBxcWHatGk0aNCg3DKn\nT59m3LhxeHl5MWPGjKuut2fPHl588UUAmjdvzuTJk29uKhGxGT+e/IFBq3qTez633POerl7UrVGX\nUP/by8r5f8s6yLMObi5ul91uQIA3WVlnKmMEEVNZVORJSUn4+PiQkJDA5s2bSUhIYPr06eWWmTRp\nEu3atWPPnj3XXG/q1KnExcURFhbG+PHj2bRpE926dbu5yUSkyjt0+meGrRlM7vlcYjs8T3idDtT9\n7/lo3bdb5PpYdKwpNTWViIgIADp16kRaWtoly0yZMoV27dpdc72ioiKOHj1KWFgYAN27dyc1NdWS\nWCJiQzILjhO5ZhCZhceZ0jmeceF/p2v9uwnxa6YSF7kBFhV5dnY2/v7+v23A2RknJyeKiorKLVOj\nxqVfGrncetnZ2fj4/P8f2lq1apGVlWVJLBGxETnnTjFszWB+yTvE+PAJPNZqlNmRRGzWNQ+tJyYm\nkpiYWO659PT0co8Nw7DozS+33vVsy8/PE1dXF4ve82oCArytvs2qTjM7hqo0c0FRAQNXD+fHUz/w\nVPuneKXPNJycnCrkvarS3JVFMzueaxZ5ZGQkkZGR5Z6LjY0lKyuL0NBQiouLMQwDN7fLf+Hk9wID\nAy9ZLyAggNzc//+SS2ZmJoGBgVfdTk5O4TXf60Y54hdjNLNjqEozny85z0Nrh/H1r19zf8gwng+f\nQnZ2foW8V1Wau7JoZvt2pR9YLDq03rlzZ5KTkwFISUmhY8eOFq9XrVo1goOD2bFjBwAbNmygS5cu\nlsQSkSqspLSEUZ8+yqZfU+jZqDczerylXwkTsQKLvrXet29ftmzZQlRUFG5ubsTHxwMwe/Zs2rdv\nT1hYGNHR0eTl5ZGZmcmIESMYNWrUFdeLi4tj4sSJlJaW0qpVKzp16mS9CUXEdIZh8LdNz7DmwCru\nqteZd3ot0NXRRKzEybD0BLeJKuIwiiMdnrlIMzuGqjDzP1InMvOb6YQFtGbFwDX4VPet8PesCnNX\nNs1s36x6aF1E5HrNSHudmd9M59aaISzpv6JSSlzEkajIRaTCvLd7HlO+nsQtNeqzdMAqanvUNjuS\niN1RkYtIhVi1fzl/2/QMtdxrkTjgI+p7N7j2SiJyw1TkImJ1nx3+hNEbH8OrWg0+HLCSW/1CzI4k\nYrdU5CJiVVuPfc3DyQ/h4uTC+30/JCygtdmRROyabmMqIlbzffYuHlwbSVFJEQv6fECnW/5gdiQR\nu6ciFxGrOHj6AA+suY+8otO8ee879Gzcx+xIIg5Bh9ZF5KYdy89g2OrBZJ09wbQurzC02QNmRxJx\nGCpyEbkpp86dZNiawRw+8wsTOjxHTMvHzY4k4lBU5CJisfyiM0Ql3c/enD08HjaKce3+bnYkEYej\nIhcRi5y7cI4/ffxHvjmRxvDQB5nc+aUKux2piFyZilxEbtiF0gs8/skjfHl0E32a9Oe1u/+tO5mJ\nmER/8kTkhpQapYz7fAwf/5xEl1u68XbEu7g66xdgRMyiIheR62YYBpO+imPJnkW0CWzLgj4f4O7q\nbnYsEYemIheR6/b6zld4+7s3ae4XyuL+y6nhdvnbKopI5VGRi8h1mbtrNvHbptDAuyFLB6zC372W\n2ZFEBBW5iFyHZfs+5Nkv/0qARyCJAz+ibo16ZkcSkf9SkYvIVW049DFjNj6Bj5svHw5YSbBvU7Mj\nicjvqMhF5IpSM77iz+v/hJuLG4v6JdKidkuzI4nI/9DvjIjIZX2X9S0PrXuAEqOEhX2W0LHunWZH\nEpHLUJGLyCV+ytnP8KQh5Bed4e2Id+nRMMLsSCJyBSpyESnn6JlfiVwziOyz2bzSbTqDQ+43O5KI\nXIXOkYtImeyz2USuGcTR/F95/s4X+dMdj5gdSUSuQUUuIgCcKcpjeNIQfsrdz+jWTzOmzV/MjiQi\n10FFLiKcvXCWEeuG813Wtzx420gm3vUP3clMxEaoyEUcXHFJMY9tiGZLxmYGNB3Mq93eUImL2BAV\nuYgDKzVKeTplFOsPfUy3+t158953cHF2MTuWiNwAFbmIgzIMg+c3T2DZvg9pF9SeeX0WUd2lutmx\nROQGqchFHNQr26cxZ9fb3OZ/Ox/0S6RGtRpmRxIRC6jIRRzQ7PQ3eXVHPI18GrN0wCr83P3NjiQi\nFlKRiziYD/d8wPNfxRLkWYfEAR8R5FXH7EgichNU5CIO5OOf1/JMymhqVq/J0gGraOzbxOxIInKT\nLLpEa3FxMbGxsWRkZODi4sK0adNo0KBBuWVOnz7NuHHj8PLyYsaMGVddb8SIERQWFuLp6QnAhAkT\naNGixU2OJiK/t/noFzy2IZrqLtX5oN8ybqt1u9mRRMQKLNojT0pKwsfHh8WLF/PEE0+QkJBwyTKT\nJk2iXbt2173etGnTWLhwIQsXLlSJi1jZtyfSGLFuOKVGKfP7fEB4nQ5mRxIRK7GoyFNTU4mI+O1u\nSJ06dSItLe2SZaZMmXJJkV/PeiJiXT9m/cjwpCGcvVDIfyLmcneDHmZHEhErsujQenZ2Nv7+v33L\n1dnZGScnJ4qKinBzcytbpkaNS3+V5UrrAcyYMYOcnByaNm1KXFwc7u7uV3x/Pz9PXF2tf9GKgABv\nq2+zqtPM9u2X3F+IeDeCU+dOMWfAHB5pO8LsSJXKkT7rizSz47lmkScmJpKYmFjuufT09HKPDcOw\n6M0vrjdy5EiaN29Ow4YNmTRpEosWLSImJuaK6+XkFFr0flcTEOBNVtYZq2+3KtPM9u1E4QkGruzF\n0TNHmXTXFAY2GOYws4NjfdYXaWb7dqUfWK5Z5JGRkURGRpZ7LjY2lqysLEJDQykuLsYwjHJ741cS\nGBh42fUuHm4H6NGjB+vWrbvmtkTkyk6fz2V40hAOnj7As394ltFhY82OJCIVxKJz5J07dyY5ORmA\nlJQUOnbsaPF6hmEQHR1NXl6t02SnAAAa80lEQVQeAFu3biUkJMSSWCICFBYX8tC6B/g++ztG3v4I\nU3tMNTuSiFQgi86R9+3bly1bthAVFYWbmxvx8fEAzJ49m/bt2xMWFlZWzpmZmYwYMYJRo0Zddj0n\nJyeGDRtGdHQ0Hh4eBAUFMWbMGKsOKeIoCosLeTj5QbYeS2XwrUN4uWuC7mQmYuecDEtPcJuoIs6H\nONJ5los0s33JPZfDg+uGsf34Vu5t2JP5fT7AzcXNrme+GkecWzPbtyudI9eV3UTswPGCYwxa1Yft\nx7cyJGRoWYmLiP1TkYvYuIOnD9B/RU9+PPUDMS0f481756jERRyIRefIRaRq2JWVzgNJQ8g+m8Xf\n28cxPnyCzomLOBgVuYiN2nJ0MyM+Hk5+0Rle7voaD7f4s9mRRMQEKnIRG/Txz2t5bEM0pUYpb0e8\ny+CQ+82OJCIm0TlyERuz+Mf3eTj5QVycXHm/71KVuIiDU5GL2JCZ37zB0ymj8HXzZfmg1XRveI/Z\nkUTEZDq0LmIDDMPgH6kTmfXtG9TzuoUPB6ykuX+o2bFEpApQkYtUcRdKLzD+87Es3vM+t9YMYemA\nVdT3bmB2LBGpIlTkIlXY2QtnefyTR0j+eS2tA9rwQf/l1PaobXYsEalCVOQiVVTe+dOM/DiKLRmb\n6VL/bhb0XkQNN8e+77KIXEpFLlIFnSg8wfCkIXyf/R0Dmg7mzXvfobpLdbNjiUgVpG+ti1Qxv+Qd\nYsDKnmW3IZ0dMU8lLiJXpD1ykSrkh5O7eWDNfWQWHucv7f5KbIcXdMlVEbkqFblIFbH12Nc8tG4Y\np8/nMqVzPI+1GmV2JBGxASpykSrgk0PJ/HnDnygqKWLWPbOJbD7c7EgiYiN0jlzEZIl7lzDy4ygA\n3uuzWCUuIjdERS5iotnpbzJ642PUcPNm6YCPiGjc2+xIImJjdGhdxASGYRC/7Z+8vvNVgjzr8OGA\nldxe6w6zY4mIDVKRi1SyktISJnwxnvd+eJfGPk1IHPgRjXwamx1LRGyUilykEp0vOc+oTx9lzYFV\ntKgdxpL+Kwj0DDQ7lojYMBW5SCXJLzrDn5If5MtfP+euep1Z2GcJPtV9zY4lIjZORS5SCbLPZvPH\npPv5Nusbejfuy9s95+Hh6mF2LBGxAypykQr265kjDFszmJ9y9xMV+hAJd8/A1Vl/9ETEOvTrZyIV\naO+pPfRbEcFPufsZ3fpppnefpRIXEavS/1FEKsjOzO38MWkoOedzmHjXP3mqzdNmRxIRO6QiF6kA\nKYc38nDyQ5wrOcsb3d8k6raHzI4kInZKRS5iZav2L2f0xsdwdnJmXu9F9GnSz+xIImLHdI5cxIre\n/f4dHv/kEaq7uPNh/5UqcRGpcNojF7ECwzB4dUc8r2yfRm2PAD7sv4KWAa3MjiUiDkBFLnKTSo1S\nntv8d+bumk1D70YsHbCS4Jq3mh1LRByEilzkJhSVFDH2sydYsX8Zt/nfzocDVlLHq67ZsUTEgVh0\njry4uJjx48cTFRXFQw89xJEjRy5Z5vTp08TExDB27Nhyz2/bto277rqLlJSUsuf27NnD8OHDGT58\nOJMmTbIkkkilKyguYMS6B1ixfxnt63Tko8Efq8RFpNJZVORJSUn4+PiwePFinnjiCRISEi5ZZtKk\nSbRr167cc4cPH2bevHm0bdu23PNTp04lLi6OJUuWkJ+fz6ZNmyyJJVJpcs6dYujqgaQc2ci9DXuS\nOOAjarr7mR1LRByQRUWemppKREQEAJ06dSItLe2SZaZMmXJJkQcEBDBz5ky8vb3LnisqKuLo0aOE\nhYUB0L17d1JTUy2JJVIpjuVnMHBlb3ZmbmdoswdY0GcxntU8zY4lIg7KonPk2dnZ+Pv7A+Ds7IyT\nkxNFRUW4ubmVLVOjRo1L1vPwuPQmETk5Ofj4+JQ9rlWrFllZWVd9fz8/T1xdXSyJflUBAd7XXsjO\naOYbs+/kPgZ81JPDpw/zdMenea3Xazg7Vf3f4nTEzxkcc27N7HiuWeSJiYkkJiaWey49Pb3cY8Mw\nrBboeraVk1Notfe7KCDAm6ysM1bfblWmmW9M+olvGJ40hJPnTvJshxd4pu1fOZldYOWE1ueInzM4\n5tya2b5d6QeWaxZ5ZGQkkZGR5Z6LjY0lKyuL0NBQiouLMQyj3N74jfD39yc3N7fscWZmJoGBgRZt\nS6SifPnrJkZ+HEVhcQGvdJvOn+54xOxIIiKAhefIO3fuTHJyMgApKSl07NjR4gDVqlUjODiYHTt2\nALBhwwa6dOli8fZErC3pwGqiku6nqOQ87/ScrxIXkSrFonPkffv2ZcuWLURFReHm5kZ8fDwAs2fP\npn379oSFhREdHU1eXh6ZmZmMGDGCUaNGcf78eebOncvBgwfZvXs3Cxcu5N133yUuLo6JEydSWlpK\nq1at6NSpk1WHFLHEmaI83v/hPSanPo+7iwcL+nxAtwbdzY4lIlKOk2HNE9yVpCLOhzjSeZaLNPOl\nTp49yfpD60g68BFf/Po5RaVF+Lv7s7jfctoEtbvielWZI37O4Jhza2b7ZvE5chF7dyw/g3U/J7Hu\n4Bq2ZGymxCgB4I5aLekXPICo0Ie4xbu+ySlFRC5PRS4O6Ze8QyQdWM3ag6vZkbmt7Pl2QeH0Cx5E\n3+D+BPs2NTGhiMj1UZGLw9h3ai9v/5jM0l3L2JX9269QOjs507leF/oFD6Bv8ADq1bjF5JQiIjdG\nRS52yzAMdmWns/bgapIOrGZ/7j4AqjlXo0fDe+kfPIhejfsS4BlgclIREcupyMWulBql7Di+naSD\nH7Hu4BoOn/kFAA9XD/o2GUBU62Hc6d8N3+o1TU4qImIdKnKxeRdKL7AlYzNrD65m3cEkMguPA1Cj\nmjdDQobSL3gQPRrei1c1L4f6hquIOAYVudik8yXn+eJICkkHV5P881pyzucA4O/uzx9DR9AveABd\nG3Snukt1k5OKiFQsFbnYjILiAj47/AlrD65mw6H15Bf/tmcd5FmHR1o8Sr/ggdxVrzOuzvrPWkQc\nh/6PJ1Xa6fO5bDiUTNLB1aQc/pRzJecAaOjdiBG3R9O/6UDaBbW3iTuQiYhUBBW5VDlZhVkkH1rL\n2oOr+fLXTRSXFgPQzK85/YIH0D94EC1qh+Hk5GRyUhER86nIpUrIyD/KuoNrSDq4mq+PbaHUKAUg\nLKA1/ZoMoF/wQJr5Nzc5pYhI1aMiF9P8fPogSQdXs+7ganZm7ih7vn2djvQLHki/4AE08mlsXkAR\nERugIpdKYxgGe079+NsFWg6u5oeT3wPg4uRCl/p3/3Z1tSb9qeNV1+SkIiK2Q0UulWJ39vc8tfFx\ndp/cBYCbsxsRjXrRP3gQPRv3oZZHLZMTiojYJhW5VLjFP77PhC/Gca7kHH2bDGDgrYOJaNQLbzcf\ns6OJiNg8FblUmMLiQp798q8s3vM+Pm6+vN1zHn2a9DM7loiIXVGRS4U4mPsTj6wfyQ8nvycsoDVz\nei6gsW8Ts2OJiNgdXUVDrG7NgVXcm9iNH05+z5/uiCHpvg0qcRGRCqI9crGaopIiJm95nnd2/QdP\nV0/euncO9zcbZnYsERG7piIXq/j1zBEe3fAndmbuoJlfc+b2Wkhz/1CzY4mI2D0Vudy0jb9sYNSn\nj5JzPof7Q4bxyt3TqVGthtmxREQcgopcLFZSWsK/tk/l9Z2v4ubsxivdpjPy9od1DXQRkUqkIheL\nZBZm8uQnMWw++gUNfRrzbq/3CAtobXYsERGHoyKXG7bl6GYe++RhThRm0rtJP/7d4y18q9c0O5aI\niENSkct1KzVKmfnNdF7a+g+ccGLSXVMY1XqMDqWLiJhIRS7XJefcKcZsfIINvyRTx6sus3vO5866\nd5kdS0TE4anI5Zq+ydzJnzf8iSNnDtO1fnfeuncOAZ4BZscSERF0ZTe5CsMwmLtrNv1X9uTXM0f4\na3gsH/ZfoRIXEalCtEcul5VfdIbxn49l5U/LqeVeizfvnUP3hveYHUtERP6Hilwu8ePJH4hZP4Kf\ncvfTvk5H3uk5n3o1bjE7loiIXIYOrUs5S/Ysovfy7vyUu58nWj3FqkHrVOIiIlWYRXvkxcXFxMbG\nkpGRgYuLC9OmTaNBgwblljl9+jTjxo3Dy8uLGTNmlD2/bds2nn76aV566SW6d+8OwIgRIygsLMTT\n0xOACRMm0KJFC0tnEgucvXCWuC//xqIf38PbzYd5vefQL3iA2bFEROQaLCrypKQkfHx8SEhIYPPm\nzSQkJDB9+vRyy0yaNIl27dqxZ8+esucOHz7MvHnzaNu27SXbnDZtGs2aNbMkjtykg6cPEJM8kt0n\nd9Gydivm9FpAE99gs2OJiMh1sOjQempqKhEREQB06tSJtLS0S5aZMmUK7dq1K/dcQEAAM2fOxNvb\n25K3lQqQdGA1EYnd2H1yFyNuf5i1Qz5RiYuI2BCL9sizs7Px9/cHwNnZGScnJ4qKinBzcytbpkaN\nS+9+5eHhccVtzpgxg5ycHJo2bUpcXBzu7u6WRJPrVFRSxF+S/8L0rdPxdPVk5j1vM6x5lNmxRETk\nBl2zyBMTE0lMTCz3XHp6ernHhmHcVIiRI0fSvHlzGjZsyKRJk1i0aBExMTFXXN7PzxNXV5ebes/L\nCQhwjCMFR04f4YFlD5D6ayqhtUNZFrmMOwLvMDtWpXGUz/n3HHFmcMy5NbPjuWaRR0ZGEhkZWe65\n2NhYsrKyCA0Npbi4GMMwyu2N36iLh+kBevTowbp16666fE5OocXvdSUBAd5kZZ2x+narms8Of8Ko\nTx/l1LlTRLWIYupdCdRwquEQs4PjfM6/54gzg2POrZnt25V+YLHoHHnnzp1JTk4GICUlhY4dO1oc\nzDAMoqOjycvLA2Dr1q2EhIRYvD25vJLSEuK3TSEqaSj5Rfm83PU1Fg1ZRI1ql54CERER22HROfK+\nffuyZcsWoqKicHNzIz4+HoDZs2fTvn17wsLCyso5MzOTESNGMGrUKM6fP8/cuXM5ePAgu3fvZuHC\nhbz77rsMGzaM6OhoPDw8CAoKYsyYMVYd0tFlFWbxxKcxfPnr5zT0bsScXgtoHdhWdy0TEbEDTsbN\nnuA2QUUcRrHXwzNfZ2zh0Q3RZBYep1fjPvy7x3+o6e4H2O/MV6OZHYcjzq2Z7duVDq3rEq12yjAM\nZn77Bi99PRmAF+76B6Nbj8XZSRfzExGxJypyO5R7Loexnz1J8qF1BHnWYXbPedxVr7PZsUREpAKo\nyO1M+olviFk/ksNnfqHLLd14K2IugZ6BZscSEZEKouOsdsIwDOZ9P4d+KyI4cuYw48L/ztIBq1Ti\nIiJ2TnvkdiC/OJ+/fj6WFfuX4e/uz5v3vkOPhhHXXlFERGyeitzG7T21h5j1I9iXs5d2Qe2Z03MB\nt3jXNzuWiIhUEh1at2GJe5fQa9nd7MvZy+Nho/ho8McqcRERB6M9chu0P2cfs755gw/2LMTbzYe5\nvRYyoOkgs2OJiIgJVOQ2IiP/KCv3L2fF/kR2Zf9205o7arVkbu/3CPZtanI6ERExi4q8Css5d4o1\nBz5ixf5EUjO+wsDA1dmVno16c1/IUPoFD8TdVbd7FRFxZCryKqaguIANhz5mxf5EPjv8KcWlxQDc\nVa8zQ0IiGdB0EP7utUxOKSIiVYWKvAooLilm06+fsXxfIh//vJbCCwUAtKgdxpCQSAbfOoT63g1M\nTikiIlWRitwkpUYp245vZcW+paw+sJJT504B0MinMfeHjOK+kEia+4eanFJERKo6FXkl2539PSv2\nJ7Jy/zJ+zT8CQG2PAB5t+QRDmkXSNjBctxcVEZHrpiKvBL/kHWLVf79x/uOpHwCoUc2bB5r/kfub\nDeMPt3TF1VkfhYiI3Di1RwXJKsxi9YGVrNifyPbjWwFwc3ajb5MB3N8sknsb9cLD1cPklCIiYutU\n5FaUX3SGdT8nsWJ/IpuOpFBilOCEE13q3839IZH0Cx6Ab/WaZscUERE7oiK/SedLzvPZ4U9ZsS+R\n9YfWca7kHABtAtsyJCSSQbcOoY5XXZNTioiIvVKRW6CktITUY1+xYl8iaw5+xOnzuQA0rXkr94cM\nY0jIUIJr3mpyShERcQQq8utkGAbfZX3L8v2JrPppOccLjgFQx6sufwwdwf3NImlZu5W+cS4iIpVK\nRX4NB3N/Yvn+RFbsT+RA7k8A+FavyYjboxkSEsmddTvh4uxickoREXFUKvLLOF5wjFU/LWfFvkS+\nzfoGAHcXdwY1HcL9zYbRveE9VHepbnJKERERFXmZ3HO5LPphESv2J7L56BcYGLg4udCj4b0MCYmk\nb5P+1HDzNjumiIhIOQ5f5PnF+YxPGcPan9dQVFIEQPs6HRkSEsnApvcR4BlgckIREZErc/giP3X2\nJOt+TiLEP4TBwUMZHHI/jXwamx1LRETkujh8kTf0acTPjx6jbpAfWVlnzI4jIiJyQ5zNDlAV6Drn\nIiJiq1TkIiIiNkxFLiIiYsNU5CIiIjZMRS4iImLDVOQiIiI2zKKvaxcXFxMbG0tGRgYuLi5MmzaN\nBg0alFvm9OnTjBs3Di8vL2bMmAHAhQsXeO655zh8+DAlJSX8/e9/Jzw8nD179vDiiy8C0Lx5cyZP\nnnxzU4mIiDgIi/bIk5KS8PHxYfHixTzxxBMkJCRcssykSZNo165duec++ugjPDw8WLx4MVOnTiU+\nPh6AqVOnEhcXx5IlS8jPz2fTpk2WxBIREXE4FhV5amoqERERAHTq1Im0tLRLlpkyZcolRT5w4ECe\nffZZAPz9/cnNzaWoqIijR48SFhYGQPfu3UlNTbUkloiIiMOx6NB6dnY2/v7+ADg7O+Pk5ERRURFu\nbm5ly9SoUeOS9apVq1b2zwsWLKB///7k5OTg4+NT9nytWrXIysqyJJaIiIjDuWaRJyYmkpiYWO65\n9PT0co8Nw7ihN120aBG7d+/mP//5D6dOnbrhbfn5eeLqav17gAcEON7dzTSzY3DEmcEx59bMjuea\nRR4ZGUlkZGS552JjY8nKyiI0NJTi4mIMwyi3N341iYmJfPbZZ7z55ptUq1at7BD7RZmZmQQGBl51\nGzk5hdf1XjciIMDb4a61rpkdgyPODI45t2a2b1f6gcWiQ+udO3cmOTmZLl26kJKSQseOHa9rvSNH\njrBkyRLef/99qlevDvx2uD04OJgdO3YQHh7Ohg0bGDFixFW3U1E/fTniT3Wa2TE44szgmHNrZsfj\nZNzocXGgpKSE559/nkOHDuHm5kZ8fDx169Zl9uzZtG/fnrCwMKKjo8nLyyMzM5OQkBBGjRpFamoq\na9eupV69emXbmjt3LocPH2bixImUlpbSqlWrsi/EiYiIyNVZVOQiIiJSNejKbiIiIjZMRS4iImLD\nVOQiIiI2TEUuIiJiwyz69TNbYukNXq60ni3c4OV6Zl69ejULFizA2dmZYcOGERkZSWFhIbGxsWRn\nZ+Ph4UF8fDwBAQGMGDGCwsJCPD09AZgwYQItWrQwY7QrsvbM9vw5Z2ZmEhcXR1FREaWlpTz77LO0\naNGCHj16UKdOHVxcfrvY0quvvkpQUJAZo12VtefesmULr732Gi4uLnTt2pXRo0ebNNmVWTrzW2+9\nxZYtWwAoLS0lOzub9evX28Rnbe2ZbeFztphh51asWGG8+OKLhmEYxpdffmk8/fTTlyzz9NNPG7Nm\nzTLGjBlzzfUeeughIz093TAMwxg3bpzx+eefV/QIN+xaMxcUFBg9e/Y08vLyjLNnzxr9+vUzcnJy\njHnz5hn/+te/DMMwjO3btxvPP/+8YRi/zbx3797KHeIGVcTM9vo5x8fHG4sXLzYMwzB27txpPPLI\nI4ZhGEb37t2N/Pz8yh3CAtaeu0+fPkZGRoZRUlJiREVFGfv376/cga6DpTP/7zbeeecdwzBs47O2\n9sy28Dlbyu4PrVt6g5fLrWcrN3i51szp6em0bNkSb29v3N3dadu2LWlpaRw6dKhstvDwcHbu3Fnp\n2S1lzZnt/XP28/Mru5piXl4efn5+lZ79Zlhz7iNHjuDr60vdunVxdnamW7dudvVZX3ThwgUWL17M\nQw89VKm5b4Y1Z7aVz9lSdn9o3dIbvFxuvezsbJu4wcu1Zv796/DbneiysrJo1qwZmzZtolevXmzb\nto2MjIyyZWbMmEFOTg5NmzYlLi4Od3f3yh3qGqw5s63cyMfSmaOjoxk6dCirVq0iPz+fxYsXly0z\nadIkjh49Srt27Rg/fjxOTk6VO9R1sObcWVlZlyx75MiRyh3oOlg680UbNmzgD3/4Q7k/t1X9s7bm\nzLbyOVvKroq8Im7wcrX1LN2WNVlj5ouvDx06lL179xIVFUWHDh3K/sMfOXIkzZs3p2HDhkyaNIlF\nixYRExNjxSluTGXMfCPbqgzWnHnOnDn06dOHJ598kpSUFF5++WVmzpzJ2LFj6dKlC76+vowePZr1\n69fTu3dv6w5ygyp67kceecS6ga3AmjNftHz58nLf86hqn3VlzGzP7KrIrXmDl8DAwEvWCwgIuOEb\nvFQ0S2YODAwkOzu77PGJEydo3bo1bm5uZf/hFxQUsHHjRoCyw1sAPXr0YN26dRU50jVV9MyW3Min\nollz5k8++YRnnnkG+O2+CRfnHzx4cNmyXbt2Zd++faYXeUXP/b/L2ttnDVBYWMjx48epX79+2etV\n7bOu6Jmr4udsTXZ/jvziDV6AG7rBy+XW+/0NXuC3QzddunSpmOA34Vozt2rVil27dpGXl0dBQQFp\naWmEh4ezadMmpk+fDvz2bdAuXbpgGEbZdfMBtm7dSkhISOUOdB2sObO9f86NGjUq29v57rvvaNSo\nEWfOnCEmJoaioiIAtm/fXiU/Z7Du3PXr1yc/P59ff/2VCxcukJKSQufOnSt9pmuxdGaAPXv2EBwc\nXLasrXzW1pzZVj5nS9n9tdYtvcFLhw4dLrveTz/9VOVv8HKtmdu0aUNycjJz587FycmJhx56iIED\nB3Lu3DnGjh1Lbm4uvr6+vPbaa3h7e7Nu3TrmzJmDh4cHQUFBTJ06FQ8PD7PHLMfaM9vz53zixAme\ne+45zp07B8Bzzz1HaGgoCxYsYNWqVVSvXp3bb7+dF154ocqdNwXrz719+3ZeffVVAHr27GnqaaMr\nsXRmoOxXr35/mNkWPmtrz2wLn7Ol7L7IRURE7JndH1oXERGxZypyERERG6YiFxERsWEqchERERum\nIhcREbFhKnIREREbpiIXERGxYSpyERERG/Z/Ilbe7c7YKD0AAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jrsUps0nu8vj",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "** Question **
\n",
+ "Why did I created a session to plot the graph?
\n",
+ "[Ans] sess N/A"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "P3-iuxE4sjAf",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the placeholders\n",
+ "\n",
+ "# Placeholders?\n",
+ "# The input to the model changes on iteration\n",
+ "# So we cannot have a constant in the input as we did before\n",
+ "# And thus we need placeholders which we can change on each \n",
+ "# iteration of the training\n",
+ "\n",
+ "x = tf.placeholder(tf.float32, name='x')\n",
+ "y = tf.placeholder(tf.float32, name='y')"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "8hPRkaoxvRyV",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the linear regression model\n",
+ "\n",
+ "# tf.Variable?\n",
+ "# We define the model parameters as tf.Variables\n",
+ "# as they get updated throghout the training.\n",
+ "# And variables denotes something which changes overtime.\n",
+ "\n",
+ "W = tf.Variable(np.random.random_sample(), name='weight_1')\n",
+ "b = tf.Variable(np.random.random_sample(), name='bias_1')\n",
+ "\n",
+ "pred_y = (W*x) + b"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "cSw1P8bkv96r",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the loss function\n",
+ "# We are going to use the mean squared loss\n",
+ "loss = tf.reduce_mean(tf.square(y - pred_y))"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "5G4uQqjsygNj",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the optimizer\n",
+ "# And specify the which value (i.e. loss) it has to minimize\n",
+ "optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "ttI7ZT-ozAm1",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 437
+ },
+ "outputId": "56c4200e-11b0-434c-e9df-5f8e519da3e8"
+ },
+ "cell_type": "code",
+ "source": [
+ "# So the graph is now built\n",
+ "# Now let's execute the graph using session\n",
+ "# i.e. lets train the model\n",
+ "\n",
+ "# What it is to train a model?\n",
+ "# To update the paramters in the graph (i.e. tf.Variables)\n",
+ "# So that the loss is minimized\n",
+ "\n",
+ "# Okay let's start!\n",
+ "with tf.Session() as sess:\n",
+ " # We need to initialize the variables in our graph\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ " \n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ " \n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ " \n",
+ " \n",
+ " print ('The final loss is: ', final_loss)\n",
+ " \n",
+ " # Plotting the final predictions against the true predictions\n",
+ " plt.plot(test_X, test_Y, 'g', label='True Function')\n",
+ " plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()"
+ ],
+ "execution_count": 17,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.07932834\n",
+ "Loss after epoch 20 is 0.079302244\n",
+ "Loss after epoch 40 is 0.079276174\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.073968284\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAecAAAFKCAYAAAAnj5dkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3Xd4VGXexvHvpJKeTJgESKGEEJog\nRRRQBAyCsLoW1oVXRAVsgGIHYwmuK7IuYi+I7OoqahRxRVYBC9iIoIARghAIEAKhTCqppJ33j8BA\nIIVgkpkM9+e6uDInpz2/DJk75znlMRmGYSAiIiIOw8XeDRAREZHqFM4iIiIORuEsIiLiYBTOIiIi\nDkbhLCIi4mAUziIiIg7Gzd4NOM5qzbfr/oOCvMnJKbJrG5qSs9cHzl+j6mvZnL0+cP4aG7s+i8Wv\n1nk6cj7Gzc3V3k1oUs5eHzh/jaqvZXP2+sD5a2zO+hTOIiIiDkbhLCIi4mAUziIiIg5G4SwiIuJg\nFM4iIiIORuEsIiLiYBTOIiIiDsZhHkLiiF566Tm2b/+d7OwsSkpKaNcuDH//AObM+WejbH/s2CsJ\nCQnFxeXE30gvv/zGH97uDz98y4UXDuLIkTwWLVrAQw898oe3KSIizeeMwjklJYWpU6dy8803M2HC\nhGrz1q5dy/z583F1dWXIkCFMmzYNgDlz5pCUlITJZCIuLo5evXo1fuub2F133QvA559/xq5dqUyf\nfk+j72PevBfx9vZu1G1+8MFi+va9gODg1gpmEZEWqN5wLioq4sknn2TgwIE1zv/73//OokWLCA0N\nZcKECYwcOZLs7GzS0tJISEggNTWVuLg4EhISGr3x9rJx4y988MG7FBUVMX36vdx//3T+97+vAXj0\n0Ye49trr6dq1G3PmPEF+fj4VFRXcc8+DdO4cfUbbHzPmstO2t2nTBgoLC9i7N439+/dx9933M3Dg\nYFas+B9LliRgMpkYN+4GysrK2Lp1Cw88cDezZj3GE088yqJF77Bu3TqeeWYebm5uWCwhPPzw43z1\n1Up+++1XcnNz2Ls3jf/7vxv505+ubrKfm4iInJl6w9nDw4OFCxeycOHC0+alp6cTEBBA27ZtAbj0\n0ktJTEwkOzub2NhYAKKiosjLy6OgoABfX9+zbujstY/yWep/z3r9mlwZdTWzB/39rNZNTd3J++8v\nxcPDo8b5H374PhdeOIgrr7ya3bt38cIL83j++Vf/SHM5fPgQ8+a9yE8/reXTTz+md+/zeeutN3n7\n7fcpLS3jqafimTt3Pm+++Trz5r1IXl6ubd34+HjmzXuJ0NA2zJ//D778cgUmk4nU1J28/vq/2Lcv\nnfj4OIWziJxzSitK+WTHEtxc3OgcGE1UYGd8PWp/7nVzqDec3dzccHOreTGr1YrZbLZNm81m0tPT\nycnJoUePHtW+b7Va6wznoCDvOp9b6u3lgYuLqb7mNoi3l0e1B4/X9hByP79WeHufWDYw0Jvu3bsR\nFhYMgMlkss3z9HQnMNCb7duTyc7OZvXqVQAcPVp82vZdXV14+OF7cXWtqjsoKIgXX3yxxu35+Hgy\ncOCFWCx+xMR05OjRYvLyDhMd3ZnwcAsAixYttG23dWtfXF3LcHNzwd29ApPJRM+eVUfuQ4dews8/\n/0z37t254IJ+tGkTiJ+fO8XFhXU+iL0laOntr4/qa9mcvT5oeTVaC62M//A6vt/7fbXvt/VtS5fg\nLsQExxDTOoYuwV241P/SZquvWS4IMwyj3mXqG+njoT6P81CfxxurSTbHR8OyWPxqHRkrP7+EoqJS\n2/zc3CIMw2SbNgzD9rqwsNg2/6677qdnzxPn2k/dfkVFJU8//Vy1c85Wa36N2yssPIq7uxdWaz45\nOYWUlpaTl1dCSUlpjdvNzCwgL6+Q8vJKsrIKq20zK+sIJSXl5OeXUFpaidWaT1FRERUVlXYfHeyP\nqOs9dAaqr2Vz9vqg5dW4NSuZiZ+PY29+Gn/q9GcGh11Mau5OdubuIDV3J9+lfce3ad/alr+yy5Us\nil3caPuvK+j/UDiHhISQmZlpmz506BAhISG4u7tX+/7hw4exWCx/ZFcOzWQyUVJSAkBKynYAunfv\nyXffraFnz17s3r2LdevWMm7chLo2U+f2atK+fQf27k2jqKgIV1dXZs68l+eeewWTyYWKigrbcv7+\n/phMJg4ePEibNm349deN9Op1frVlRETOJSt2f86dX02hsKyABy94mPv7z8TFVP3u4uLyYnbn7SI1\ndye781IZ1S222dr3h8I5PDycgoIC9u3bR5s2bVi9ejXz5s0jJyeHl156iXHjxpGcnExISMgfOt/s\n6K6+eiy33XYTHTp0IiamGwBjx/6Vp56azdSpU6isrOSeex74Q9uriZeXF5Mn38E990wF4K9//T9M\nJhN9+vRl6tTJPPLIbNuyTz75JE888Qiurq6EhYVz2WWXs2rVF2dXsIhIC2UYBi9tep6nfppNK7dW\nvHn521zV+Zoal/Vy86J7cA+6B1edpm3OngGTUU+f85YtW/jHP/7B/v37cXNzIzQ0lOHDhxMeHs6I\nESP4+eefmTdvHgCXX345kydPBmDevHn88ssvmEwm4uPj6dq1a50NsXdXSEvrjmkoZ68PnL9G1dey\nOXt94Pg1lpSXcN+au1iSkkBbn3a8M/oDelnOP+P1G7u+urq16w3n5mLvN9TR/1P9Uc5eHzh/jaqv\nZXP2+sCxazxUdIibvxjPhkO/0C+0P2+Neo9QnzYN2kZzhrOeECYiIi3WrrxUVu35gl25qRicuADZ\nqJqyTX+z9ysyCvdzXfT1PDfsZVq5tbJfo8+AwllERFqMisoKNhz6hZV7Pmflns9Jyan9otmTmTDx\nyIXx3N33Pkymxr0ttykonEVExKEVlhXybfpqVu75nC/TVpBZXHU3kJebF6M6jmFk+yvoE9oPV5Mr\nJky28K16XbUNf49ALN4t564hhbOIiDicvKO5rNqzgs92fcqavV9TUlF1e2mIdyg3dr+ZkR2u4JLw\noXi5edm5pU1D4SwiIg4hqziLFbv/x/Jdn/LdvjWUVZYBEBPUlSs6/olRHUdzfkjf0+5HdkYK5zoc\nOJDBxInjiImpug2stLSUG264iUsvHdbgbX38cQK5ubkMGTKU775bw+TJt9e43PHhHt3d3evd5q5d\nO5k//5nThpm89NILOe+83rbp4OBgXn315Qa3+VSrV3/FsGGx7Nixvc4aRETOhGEYpObu5Nt9q/l8\n12eszfiBCqPq4Ujnte7NnzpdxZ+i/kx0UBc7t7T5KZzrERnZ3hZ+R47kccstN3DRRQPx9Dy7K/2i\no2OIjo6pdf7x4R7PJJxr4+vr2yjjQp/q3XffZtiw2HprEBGpSaVRye9ZW/npwI8kZqwlMeNHrMWH\nbfP7hfbnT52uZkynK+kQ0NGOLbU/hXMD+PsHEBzcmqysLP7974W4ublz5Eguf/vbXJ555ikyMvZT\nXl7OlCl30K/fBfzyy3pefPFZzOZggoNb065dGBs3/sLSpR/y978/U+dwjy+88BrLln3CV1+twGRy\n4ZJLhjJ+/AQOHz7EY4/Nwt3dnc6dz/yvyX379jF16nQWLXoHgMmTb+Tvf/8H//rXG7RubWH79t85\ndOggjz/+d2JiurJ48dusWfM1JpMLd9wxnW3btrJzZwpxcQ8yduxfbTV8/fWXJCQsxtXVlZiYbtxz\nzwMsWrSgxuEtReTcc6Agg092fsxPGT/y04G15B49MVpeG5+2XBs9lovaDubyDqNo5xtmx5Y6lhYT\nzj6zH8Xzs8YdMvLolVdTOPvMh4w8cCCDI0fyCAkJBaqeWT1z5iOsWPE/goNb8/DDj5Obm8uMGXfw\n9tsfsGDByzz22JNER3fhgQfupl27E//xiooK6xzu0Wo9zJo1X/Pqq4sAuPPOyQwbFsvSpQlcdtnl\nXH/9eN599y127kz5wz+H0tJS5s9/mf/+dwkrVvwPb29v1qz5mgUL3iIjYz/vvvsWs2Y9xuLFbzNn\nzj/ZuPGXYzUU8cYbr/Dvf7+Ht7c3Dz10r23eqcNbKpxFzi1lFWUs+O1V5v08l6LyQgAi/TswssNo\nBrW7mIvaDaKDf8cWcVuTPbSYcLaXvXvTmD79NqBqbOtHH33CNoRm9+5Vz1vdsuU3kpI28dtvvwJw\n9OhRysrKOHDgANHRVUe355/fl6NHj9q2u2fPbiIjO+Dp2QpPz1bMnTu/2n5//z2ZffvSueuuqvO6\nRUWFHDyYwZ49uxk2rOrh63369Oenn9ae1uaCggJbmwGiojozdWrt54d79+4DgMUSytatyaSkbKd7\n9564uLgQHh7BrFmP1bheevpewsMjbaNq9enTj5SUbQD06lX1SLyQkBAKCgpq3beIOJ+1+39g5nf3\nsT1nG+ZWZh4b+ASjOowmzC/c3k1rMVpMOBfO/nuDjnIby8nnnE/l5uZu+zpx4iRGjBhVbb6Ly4kr\nCk99SqqLiyuGUVnrft3c3Bk4cDAPPfRIte8vXvw2pmNXKta2fk3nnEtLj1SbLi8vt70+Pp708Xa6\nurpQWVn/U11Npup1lZeX4enpWeM2RcT5HSw4yPQvZ/Dxjg8xYWJi90nEXfQY5lbB9m5ai+P816M3\ng+7de/LDD1VjfubkZLNgwSsAtG5tYe/ePRiGwaZNG6qtc/Jwj0ePHuWee6ZiGIZtuMeYmG5s3LiB\nkpISDMPg+efncfRoCZGR7dm2bSuArQv5TPj6+pKTk41hGGRlZZKRsa/WZWNiurF5cxLl5eVkZ2fx\n8MNVI2qdGtgREe3Zt28vRUVVXVabNm0kJqb7GbdJRJxDeWU5b/72OjEvx/Dxjg/pbenDF9d9zbyh\nzyuYz1KLOXJ2ZMOHx7Jx48/cccckKioqmDSpqkv5ttum8uijM2nTpq3tPPVx9Q33+NJLb3D99eOZ\nNu1WXFxcGDJkKJ6erfjLX8bz2GOz+O671URFRZ9xGwMCAujffwBTpkykc+foOq+2btu2HSNHjmb6\n9NswDIPbb58GQJcuMdx660TuvPNuWw3Tps3g/vvvwmRyoVev8+nd+3x++WVdg35+ItJy/XQgkbjv\nH2RL5m8EtgrkH0PmM7H7Lbi6uNa/stRKo1Id48ijqTQGZ68PnL9G1deyOVN9hmHw/f5veX7DPH7Y\n/x0A47rewAt/mo+pyDmf2AUalUpERBxQpVHJqj0reH7DP9l4uOpU3dCI4TzQ/2EGtL0Qi48f1iLn\n+APE3hTOIiJSp4rKCj5NXcoLG+bze3YyAKM7XsmMvvfRJ7SfnVvnnBTOIiJSo4yC/XyZtpJXf32R\n3Xm7cDW5MrbLX7m77310NXezd/OcmsJZRESAqjBem/EDa/f/wI8Z37M7bxcAHi4eTOw+iel9Zpzz\nj9VsLgpnEZFzSFlFGTlHc8gpySanJJu9+Wn8lLG2WhgD+Hn4c3n7UQwKu4RrOl9HW992dmz1uUfh\nLCLiZAzDYHNmEp+lfsrmzCRySrLJLskmpySHI6V5Na5zchgPbncxPVv30u1QdqRwFhFxAoZh8Jv1\nV5al/pdlqZ+QdmSPbZ6nqyfmVsGE+0VgbtWboFZmgjzNBHuZsXiFcEGbCxXGDkbhLCLSQhmGQZJ1\n07FA/i97jwWyt5sP13S+jiujruHSiKH4uvtpgIkWRuEsItICbbYmMe3r29iW/TsAPu6+XBs9liuj\nrmF4ZCxebs77MJBzgcJZRKQFMQyDf21ZSPyPcZRWlnJ152u5uvNYhkVepkB2IgpnEZEWIu9oLveu\nvovluz4luFUwL1+2gMvaX27vZkkTUDiLiLQAGw/9wm2rbmFvfhoXtR3EghH/0u1NTkxDRoqIODDD\nMHg96WWu/GQk6fl7ua//Qyz983IFs5M7oyPnOXPmkJSUhMlkIi4ujl69etnmffXVV7z22mt4eHgw\nZswYJkyYwLp165gxYwbR0VVDGnbp0oXHHnusaSoQEXFS2SVZzPhmKiv3fIHFK4RXYxdyacQwezdL\nmkG94bx+/XrS0tJISEggNTWVuLg4EhISAKisrOTJJ5/kk08+ITAwkFtvvZXY2FgABgwYwIsvvti0\nrRcRcRIl5SXsztvFztwdpObuYGfuDr7bt4aDhQe4JHwor8YuJNQ7tP4NiVOoN5wTExNtgRsVFUVe\nXh4FBQX4+vqSk5ODv78/ZrMZgIsuuoi1a9cSFhbWtK0WEWmhyirK2J6zjd+sv7I1aws7c3ewM3cn\n+/L3UmlUVlvW09WTWQMeZUbf+/WAkHNMveGcmZlJjx49bNNmsxmr1Yqvry9ms5nCwkL27NlDWFgY\n69atY8CAAYSFhbFz507uuOMO8vLymD59OoMHD65zP0FB3ri52fc/X10DXzsDZ68PnL9G1deyHC0/\nyubDm9l4YCMb121kw4ENbD60maMVR6stF+oTysWRFxMTHENMcAxdgrsQ0zqGjoEdcXd1t1Prz46z\nvYenaq76Gny1tmEYttcmk4m5c+cSFxeHn58f4eHhAHTo0IHp06dzxRVXkJ6ezsSJE1m1ahUeHh61\nbjcnp+gsmt94LBY/rFbnHSTc2esD569R9Tk+wzBIztrCl3tWsCptBUnWTZRXltvme7h40C24B70s\n59PL0puerc+jc2A0AZ6Bp2+sEnKzS4CS5ivgD3KG97AujV1fXUFfbziHhISQmZlpmz58+DAWi8U2\nPWDAAN577z0Ann32WcLCwggNDWX06NEAREZG0rp1aw4dOkRERMRZFyEi4oiKy4v5cf93rNyzgi/3\nrCCjcD8AriZXzg/pUxXErc9naMxgLETg4Vr7QYrIcfWG8+DBg3nppZcYN24cycnJhISE4Ovra5s/\nZcoU/vGPf+Dl5cXq1au55ZZbWLZsGVarlcmTJ2O1WsnKyiI0VBcyiIhzKCor4r87P+aL3cv5bt8a\nisuLAQj0DOS66Ou5vMMohkVcRmCrINs6zn5UKY2r3nDu27cvPXr0YNy4cZhMJuLj41m6dCl+fn6M\nGDGC66+/nkmTJmEymbjtttswm80MHz6cBx54gK+//pqysjJmz55dZ5e2iEhLkFWcxb+2vMG/Nr9B\nVkkWAF2CYhjRfhQjO1xB/zYDcHPRs53kjzMZJ59EtiN7/0Xp7H/VOnt94Pw1qj772ZO3m9eTXub9\nbe9SXF5MoGcgt/ScwriuE+gY0OmMtuHI9TUWZ6/Roc45i4icq349vJFXNr3IZ7v+S6VRSYRfJHf0\nnsb4bjfi6+5b/wZEzpLCWUTkGMMw2J6zjbUZP/DZzv/yY8b3APRs3YvpfWZwVdQ16raWZqH/ZSLi\nVApK81m0+Q3ySvOI8IukvX97IvzaE+4XcdqQipVGJduzt7E243t+3P8DPx34kcziE3enXBo+jOl9\n7mFI+FBMJlNzlyLnMIWziDgFwzBYlvoJj/8Yx4HCjBqXCfEOJdKvPZH+kZSUH+WnAz+SXZJtm9/O\nJ4yxXf7KoHYXMzjskjM+nyzS2BTOItLi7chJYdb3D/D9vjV4unpyf/+ZXBoxnPQjaaTn72Xvsa9p\n+WlsOryBXw6tByDMN5y/dLmcwWGXMKjdxbT376AjZHEICmcRabEKygp47pd/8nrSy5RVlnFZ5Aie\nuuQZOgVEAXBR24GnrVNeWc7BwgMYGIT7RiiMxSEpnEWkxTEMg+W7PuWxHx4mo3A/EX6R/P3ifzCq\nw+h6w9bNxY1wPz2tUBybwllEWozyynK+Tf+G15Je4bt9q/Fw8eDefg8wo+8DeLt727t5Io1G4Swi\nDs0wDLZkbebD7e+zNOUjrMWHARgWcRlPX/JPOgV2tnMLRRqfwllEHNLBwgMsSfmQj7a/z+/ZWwEI\n8gxiUs9b+UvMOPqG9Nf5YnFaCmcRcRiGYfBl2gre3LyA7/atodKoxN3FnTGdruL6mPFcFjlCozrJ\nOUHhLCJ2ZxgGy7Yv4/GvZ5Nk3QRAv9ALuD5mPH/ufA3mVsF2bqFI81I4i4jdGIbBij2fM+/nuWzO\nTMKEiT9HXcu9/R+ke3APezdPxG4UziLS7AzD4Ivd/2PeL3PZkvkbJkyM6zmOqT3vpau5m72bJ2J3\nCmcRaTaFZYWs2P0/Xt70AslZmzFh4trosdzb7yEujrnAqYcbFGkIhbOINKmS8hK+3vsl/93xMavS\nvqC4vBgXkwvXRv+F+/o9RBdzjL2bKOJwFM4i0uhKK0r5bt9qPtnxMV/s/h8FZVVHxFGBnbm683X8\npctfdX+ySB0UziLyh1QalaTn72VHznZSclLYmrWFVXu+IPdoLgARfpHc0nMKV3e+lp6te+neZJEz\noHAWkTNWVFbE13u/ZHv277YwTs3dQUlFSbXl2vi05faY/+Pq6Ov0sBCRs6BwFpF6HTmax7+3vMmC\n314hszjT9n0vNy+ig2KIDupCl6AYooNi6BIUQ+fAaFxdXO3YYpGWTeEsIrXKKs7ijd9eYdHmhRwp\nzcPfI4C7+9zHwHaDiA6KIdwvAheTi72bKeJ0FM4icpoDBRm8mvQS7yT/m6LyIlp7tebRi2ZzS88p\n+Hn427t5Ik5P4SwiNnvydvPSpudJ2LaY0spS2vmE8chF8dzQ7SYNySjSjBTOIsKOnBRe2PgsH6d8\nSIVRQQf/jtzd9z6ujxmvgSZE7EDhLHIOS87cwvMb5rEs9RMMDLqauzGj7/38ufO1uLno40HEXvTb\nJ3IO+vXwRuZv+Ccrdv8PgPNa9+befg8yutOfdIGXiANQOIucI45WHCUx40deT3qZb/Z+BVQNy3h/\n/4e4LPJy3Yss4kDOKJznzJlDUlISJpOJuLg4evXqZZv31Vdf8dprr+Hh4cGYMWOYMGFCveuISNOr\nqKzgN+uvfL//W77b9y3rDyTaHhZycdgQ7u33IBeHDVEoizigesN5/fr1pKWlkZCQQGpqKnFxcSQk\nJABQWVnJk08+ySeffEJgYCC33norsbGx7N27t9Z1ROTsZRVnUV5ZRoVRQaVRSaVRSYVRgWFUUmkY\nFJUXsv7AT3y3/1vW7v+BI6V5tnW7mXtwSfgQroq6lgFtL7RjFSJSn3rDOTExkdjYWACioqLIy8uj\noKAAX19fcnJy8Pf3x2w2A3DRRRexdu1a0tPTa11HRBpud94ubljxIF/u+vKM1+ng35E/d76GS8Iu\nZVDYJYR4hzRhC0WkMdUbzpmZmfTo0cM2bTabsVqt+Pr6YjabKSwsZM+ePYSFhbFu3ToGDBhQ5zq1\nCQryxs3Nvo/7s1j87Lr/pubs9YHz1VhWUcb8xPnM/nY2JeUlDIoYRGRAJC4mF1xNrtW+uphccHd1\np2/bvlzW8TLaB7a3d/MbzNnev1M5e33g/DU2V30NviDMMAzba5PJxNy5c4mLi8PPz4/w8PB616lN\nTk5RQ5vSqCwWP6ce6N3Z6wPnq3HDoZ+5f80MtmZtobWXhbf+/BbDQq44s3PEZbS4n4WzvX+ncvb6\nwPlrbOz66gr6esM5JCSEzMwTD7o/fPgwFovFNj1gwADee+89AJ599lnCwsI4evRoneuISO3yS4/w\n9LonWbT5DQwMJnS7iccGPkGXiPZO/cEnIifUe0Pj4MGDWblyJQDJycmEhIRU656eMmUKWVlZFBUV\nsXr1agYOHFjvOiJSsy92/4+L3x/Am5sXEBXYmU+v/oL5w14iqJXZ3k0TkWZU75Fz37596dGjB+PG\njcNkMhEfH8/SpUvx8/NjxIgRXH/99UyaNAmTycRtt92G2WzGbDafto6I1GzvkTRW7fmC5buWsTbj\nBzxcPHig/yxm9LsfT1dPezdPROzAZJzJCeFmYO/uOp0raflaSo2VRiW/WX9lxZ7PWbH7c7ZmbbHN\nuyTsUp6+ZB5dzDGnrddS6jtbqq/lc/YaHeqcs4icvUqjEmuxlYMFGaTnp/PtvtWs3PM5BwsPAODh\n4sFlkSMY2WE0IztcQVvfdnZusYg4AoWzSCPIKNjPstRP2JefzoHCAxwoyOBg4QEOFh2gvLK82rLm\nVmb+GvN/jOwwmqGRw/F11/UYIlKdwlnkD9iRk8LLm55nSUoCZZVltu+7ubjRxrst51v60ta3HW19\n2tLGpx39Qy/ggjYX4upi33v6RcSxKZxFzsLGQ7/w4sbn+GL3cgwMOgdGc0fv6fS2nE8b33ZYvCwa\n3UlEzprCWeQMGYbBmvRveGnTc/yw/zsA+ob0466+93FFxzEKYxFpNApnkTqUVZSRnLWZ9Qd+ImH7\n+2zOTAJgWMRl3N33Pga1u1ijOolIo1M4i5wk72guvxxcz/qDP7H+wDo2Hd5AUXnVo2VdTC5c3fla\n7upzL+dZetu5pSLizBTO4vTKKspYnf4VmcWZFJcXH/tXdOJrWTFF5YVsy/6d7dnbMKi69d+Eia7m\nblzQ5iIGtL2Qwe0uIcyv5ufHi4g0JoWzOK3SilIStr/HCxueZW9+Wr3Le7t5MzjsEga0uZABbS+i\nX+gFBHgGNkNLRUSqUziL0ymtKOX9be/y4sb5pOfvxdPVk0k9b+X8kL54u3nj5eaFl7s3rVxb4eXm\njZe7F16uXrT2suDu6m7v5ouIKJzFeRwtP8q/t7zJixvns79gH61cW3F7r6lM6zODNj5t7d08EZEz\npnCWFu9oxVHe3fo2L//6HPvz9+Pl5sUdvaczrc8MQr1D7d08EZEGUzhLi1VRWcHHOz7kH+ufIj1/\nL97u3kw9/26mnn83Id4h9m6eiMhZUzhLi2MYBt/s/ZInf5rN1qwteLp6cmfvu5g94lFMRV72bp6I\nyB+mcJYWZcOhn3kyMZ61GT9gwsS4rjfw0AVxhPtFYPHxw1rkvMPVici5Q+EsLcLOnB3MWfc3lu/6\nFIAR7UfyyEWz6R7cw84tExFpfApncViVRiU/7v+e97e9yyc7llBhVNAv9AIeH/g3BrYbbO/miYg0\nGYWzOJwdOSl8uP19lqQksL9gHwCdA6OJuzCeMZ2u1LOsRcTpKZzFIWSXZPHJjo/5cPt7bDq8EQA/\nD38mdLuJ62PGM6DtRRr1SUTOGQpnsZtKo5I16d/wn+R/82XaCsoqy3AxuXBZ5AiujxnPqI5j8HLT\n1dcicu5ROEuzsxZZeX/bu/xn67/Ze2QPAN2De/LXmP/j2uixhPq0sW8DRUTsTOEszcIwDBIzfuTt\n5EUs37WMssoyvNy8uKHbRG5xPhirAAAgAElEQVTqMYnzQ/rau4kiIg5D4SxNoqyijIzC/ezLT+c3\naxLvbn2LHbkpAMQEdeXmnpMZ2+WvGvVJRKQGCmc5K4ZhcLjoEDtyU9idt4v0I3tJz9/LvoJ09uWn\nc6Awg0qj0ra8h4sH10Vfz009J3Nhm4t0xbWISB0UzlKnsooy9hzZTUrOdnbmpLAjN+XY1x3klx45\nbXkXkwttfdpxQZsLCfeNINI/kvb+Hbm8wxW09mpthwpERFoehbPUaE/ebt5O/hfvb3uH7JLsavPc\nXdzpFBBF5/ChRAd2oVNgFBF+kUT4RdLWp53GRBYR+YPOKJznzJlDUlISJpOJuLg4evXqZZu3ePFi\nli1bhouLCz179uSRRx5h6dKlvPDCC0RGRgIwaNAg7rzzzqapQBpNRWUFX+1dxb+3LGT13q8xMAhu\nFcy4rjfQJagr0UFdiA6MJtK/A24u+rtORKSp1PsJu379etLS0khISCA1NZW4uDgSEhIAKCgoYNGi\nRaxatQo3NzcmTZrEr7/+CsDo0aOZOXNm07ZeGsXhosO89/t/+E/yv9lXkA7ABW0u5JaeU7gy6mo8\nXT3t3EIRkXNLveGcmJhIbGwsAFFRUeTl5VFQUICvry/u7u64u7tTVFSEt7c3xcXFBAQENHmjpXHs\nz9/Hkz/F81nqfymrLMPbzYeJ3Sdxc8/J9Gx9nr2bJyJyzqo3nDMzM+nR48TIP2azGavViq+vL56e\nnkybNo3Y2Fg8PT0ZM2YMHTt2ZNOmTaxfv57JkydTXl7OzJkz6d69e5MWImfOMAze2foWs9c+SkFZ\n/rFbm6Zwfcw4/Dz87d08EZFzXoNPHBqGYXtdUFDAggULWLFiBb6+vtx0001s27aN3r17YzabGTp0\nKJs2bWLmzJl89tlndW43KMgbNzfXhlfQiCwWP7vuv6lZLH7sztnNlM+m8M3ubwjwDGDRVYu45fxb\nnObWpnPhPXRmqq/lc/Yam6u+esM5JCSEzMxM2/Thw4exWCwApKamEhERgdlsBqB///5s2bKFsWPH\nEhUVBUCfPn3Izs6moqICV9fawzcnp+gPFfJHWSx+WK35dm1DUwpu7cMzq+fzZOJsisoLGdF+JPMu\nfYG2vu3IzCywd/MahbO/h6qvZXP2+sD5a2zs+uoK+nqH+Rk8eDArV64EIDk5mZCQEHx9fQEICwsj\nNTWVkpISALZs2UKHDh1YuHAhy5cvByAlJQWz2VxnMEvT2pWXyrC3h/Hw9w/i4erOK5e9wbujP6St\nbzt7N01ERGpQ75Fz37596dGjB+PGjcNkMhEfH8/SpUvx8/NjxIgRTJ48mYkTJ+Lq6kqfPn3o378/\n4eHhPPjgg3zwwQeUl5fz1FNPNUctchLDMMguyebD7e8zd/2TFJcXM6bTVcwd8iyh3qH2bp6IiNTB\nZJx8EtmO7N0V0hK7Y44/vSvtyG7Sjuwh7Ujasa972HskjYKyqnpae7Xm1TGvcqllpNOcW65JS3wP\nG0L1tWzOXh84f43N2a2tJ0m0MIZh8PPB9Xy8I4FPdy497eldAD7uvrT370Ckf3tigrpye+9pdIvs\n6NS/NCIizkTh3ELsyEnh45QEPt7xEWnHxkBu7WVhXNcb6BQQZQvj9v4dCW4V7NRHyCIizk7h7MAO\nFR3ivzuW8HHKh/xq3QSAt5sPY7v8lbFd/sqQ8KF6jKaIiBPSJ7sD2njoF9747TWWpX5CeWU5riZX\nYiMv57ou1zOq4xh83H3s3UQREWlCCmcHUVZRxv92LWPBb6+y4dDPAMQEdWVij1u4uvNYLN4WO7dQ\nRESai8LZzrJLsnh369ss2vwGBwozALi8/Shu7XUnQ8KH6tyxiMg5SOFsJ7tyd/LKry+xJOUDisuL\n8XH3Zcp5tzPlvNvpFNjZ3s0TERE7Ujg3s9+ztvLCxnn8d+dSKo1KIv07cOt5tzO+6wT8PTWil4iI\nKJxrlJq7gycSH6ewtAAfdx983H3xcffF18MXH3cffN398HH3Idwvgn6h/QnwDKx3m0mHN/Hchnl8\nvrtqAJAewedxb78HGNPpKlxd9GhTERE5QeF8is9SP2XGN1NtT9eqjwkTMeau9A8dQP82A+gfOoDO\nQdG4mKoeW77uwE88t+EZvtn7FQD9Qvtzb78HGdF+lM4ni4hIjRTOx5RVlBH/4yO8lvQS3m7evD5i\nEVdFXUNhWQGFZYUUlBZQWFZAwfHpsnx25Gzn54Pr2XhoA9uyf+fd398GINAzkH6hF1BUXkRixo8A\nDG53Cff2f5BLwi5VKIuISJ0UzsChwoNct3wy3+/9ns6B0fxr1Lt0NXcDIMAzsN5u6/LKcn7P3sov\nB9fz88F1/HJwPV/v/RKA4ZGx3NPvQS5qO7DJ6xAREedwzodzYsaP3LrqZg4XHeLKqKt5Ydgr+Ho0\nbDBtNxc3zmvdi/Na9+KWnlMAsBZZKSwroENAx6ZotoiIOLFzNpwNw+C1pJd5MvFxAOZfPp8boiY3\nWpezxduCBT04REREGu6cDOf80iPM+GYay3d9Soh3KG9e/jZX9h6pUZtERMQhnHPhvCVzM1NWTmRX\nXioD2w3mjcvfItQ71N7NEhERsXGxdwOai2EYvLP1La74eDi78lKZdv4MPr7qMwWziIg4nHPiyLmg\nrICHvr2XJSkJBHoGsmjkf7i8wxX2bpaIiEiNnD6ct2X/zpSVE0nJ2U7fkH4sHPk2EX6R9m6WiIhI\nrZy6Wzth23uMWjKMlJzt3N5rKsuuWalgFhERh+eUR87F5cXEff8gi3//D34e/iwa+Q5XRv3Z3s0S\nERE5I04Zzo98/xCLf/8P57XuzZsj36ZjQCd7N0lEROSMOWU4X9FxDGF+4Uw7fwat3FrZuzkiIiIN\n4pThPKLDKEZ0GGXvZoiIiJwVp74gTEREpCVSOIuIiDgYhbOIiIiDOaNzznPmzCEpKQmTyURcXBy9\nevWyzVu8eDHLli3DxcWFnj178sgjj1BWVsasWbPIyMjA1dWVp59+moiIiCYrQkRExJnUe+S8fv16\n0tLSSEhI4KmnnuKpp56yzSsoKGDRokUsXryY999/n9TUVH799VeWL1+Ov78/77//PnfccQfPPvts\nkxYhIiLiTOoN58TERGJjYwGIiooiLy+PgoICANzd3XF3d6eoqIjy8nKKi4sJCAggMTGRESNGADBo\n0CA2btzYhCWIiIg4l3rDOTMzk6CgINu02WzGarUC4OnpybRp04iNjWXYsGH07t2bjh07kpmZidls\nrtqBiwsmk4nS0tImKkFERMS5NPg+Z8MwbK8LCgpYsGABK1aswNfXl5tuuolt27bVuU5tgoK8cXNz\nbWhzGpXF4mfX/Tc1Z68PnL9G1deyOXt94Pw1Nld99YZzSEgImZmZtunDhw9jsVgASE1NJSIiwnaU\n3L9/f7Zs2UJISAhWq5WuXbtSVlaGYRh4eHjUuZ+cnKI/UscfZrH4YbXm27UNTcnZ6wPnr1H1tWzO\nXh84f42NXV9dQV9vt/bgwYNZuXIlAMnJyYSEhODr6wtAWFgYqamplJSUALBlyxY6dOjA4MGDWbFi\nBQCrV6/mwgsv/MNFiIiInCvqPXLu27cvPXr0YNy4cZhMJuLj41m6dCl+fn6MGDGCyZMnM3HiRFxd\nXenTpw/9+/enoqKCtWvXMn78eDw8PJg7d25z1CIiIuIUTMaZnBBuBvbuClF3TMvn7DWqvpbN2esD\n56/Robq1RUREpHkpnEVERByMwllERMTBKJxFREQcjMJZRETEwSicRUREHIzCWURExMEonEVERByM\nwllERMTBKJxFREQcjMJZRETEwSicRUREHIzCWURExMEonEVERByMwllERMTBKJxFREQcjMJZRETE\nwSicRUREHIzCWURExMEonEVERByMwllERMTBKJxFREQcjMJZRETEwSicRUREHIzCWURExMEonEVE\nRByMwllERMTBuJ3JQnPmzCEpKQmTyURcXBy9evUC4NChQzzwwAO25dLT07n//vspKyvjhRdeIDIy\nEoBBgwZx5513NkHzRUREnE+94bx+/XrS0tJISEggNTWVuLg4EhISAAgNDeWdd94BoLy8nBtvvJHh\nw4ezcuVKRo8ezcyZM5u29SIiIk6o3m7txMREYmNjAYiKiiIvL4+CgoLTlvvkk08YOXIkPj4+jd9K\nERGRc0i94ZyZmUlQUJBt2mw2Y7VaT1vuo48+YuzYsbbp9evXM3nyZG666Sa2bt3aSM0VERFxfmd0\nzvlkhmGc9r1NmzbRqVMnfH19Aejduzdms5mhQ4eyadMmZs6cyWeffVbndoOCvHFzc21ocxqVxeJn\n1/03NWevD5y/RtXXsjl7feD8NTZXffWGc0hICJmZmbbpw4cPY7FYqi2zZs0aBg4caJuOiooiKioK\ngD59+pCdnU1FRQWurrWHb05OUYMb35gsFj+s1ny7tqEpOXt94Pw1qr6WzdnrA+evsbHrqyvo6+3W\nHjx4MCtXrgQgOTmZkJAQ2xHycZs3b6Zr16626YULF7J8+XIAUlJSMJvNdQaziIiInFDvkXPfvn3p\n0aMH48aNw2QyER8fz9KlS/Hz82PEiBEAWK1WgoODbetceeWVPPjgg3zwwQeUl5fz1FNPNV0FIiIi\nTsZk1HQS2Q7s3RWi7piWz9lrVH0tm7PXB85fo0N1a4uIiEjzUjiLiIg4GIWziIiIg1E4i4iIOBiF\ns4iIiINROIuIiDgYhbOIiIiDUTiLiIg4GIWziIiIg1E4i4iIOBiFs4iIiINROIuIiDgYhbOIiIiD\nUTiLiIg4GIWziIiIg1E4i4iIOBiFs4iIiINROIuIiDgYhbOIiIiDUTiLiIg4GIWziIiIg1E4i4iI\nOBiFs4iIiINROIuIiDgYhbOIiIiDUTiLiIg4GIWziIiIg3E7k4XmzJlDUlISJpOJuLg4evXqBcCh\nQ4d44IEHbMulp6dz//33M2rUKGbNmkVGRgaurq48/fTTRERENE0FIiIiTqbecF6/fj1paWkkJCSQ\nmppKXFwcCQkJAISGhvLOO+8AUF5ezo033sjw4cNZvnw5/v7+PPvss/zwww88++yzPP/8801biYiI\niJOot1s7MTGR2NhYAKKiosjLy6OgoOC05T755BNGjhyJj48PiYmJjBgxAoBBgwaxcePGRm62iIiI\n86o3nDMzMwkKCrJNm81mrFbract99NFHjB071raO2Wyu2oGLCyaTidLS0sZqs4iIiFM7o3POJzMM\n47Tvbdq0iU6dOuHr63vG65wqKMgbNzfXhjanUVksfnbdf1Nz9vrA+WtUfS2bs9cHzl9jc9VXbziH\nhISQmZlpmz58+DAWi6XaMmvWrGHgwIHV1rFarXTt2pWysjIMw8DDw6PO/eTkFDW07Y3KYvHDas23\naxuakrPXB85fo+pr2Zy9PnD+Ghu7vrqCvt5u7cGDB7Ny5UoAkpOTCQkJOe0IefPmzXTt2rXaOitW\nrABg9erVXHjhhWfVcBERkXNRvUfOffv2pUePHowbNw6TyUR8fDxLly7Fz8/PdtGX1WolODjYts7o\n0aNZu3Yt48ePx8PDg7lz5zZdBSIiIk7GZJzJCeFmYO+uEHXHtHzOXqPqa9mcvT5w/hodqltbRERE\nmpfCWURExMEonEVERByMwllERMTBKJxFREQcjMJZRETEwSicRUREHIzCWURExMEonEVERByMwllE\nRMTBKJxFREQcjMJZRETEwSicRUREHIzCWURExMEonEVERByMwllERMTBKJxFREQcjMJZRETEwSic\nRUREHIzCWURExMEonEVERByMwllERMTBKJxFREQcjMJZRESkNhUVmHKycdmzG8rKmm23bs22JxER\nEXsoLcWUm4tLXi6mvGNfc3Mx5eWdeH0kD5fcqvmm3FxcjuTZvtpcey28/lazNFnhLCIijs0woKjI\nFqTHg9OUm3PidV5uVbjWFLJFRQ3aXaWPL0ZAAJVh4ZT36IkREIAREEirm29sogJPp3AWEZGmV1mJ\nKf/ISUewedVf5+XikptTLWSrzW9Al7JhMtkCtTw6BiMgsCpsAwMxAgKpPDbPCAyk0j8AI/DY/IAg\njIAAcHevcbutLH5gzW+sn0idziic58yZQ1JSEiaTibi4OHr16mWbd+DAAe677z7Kysro3r07f/vb\n31i3bh0zZswgOjoagC5duvDYY481TQUiItI8yspOBGZuzomj1OPdv6VF+B44jMuxsK1a9tjrI3mY\nDOOMd2W4u1cFaWAQRvuOx4I14Nj3AjH8j4XrseC1vQ4MxPD1A5eWfUlVveG8fv160tLSSEhIIDU1\nlbi4OBISEmzz586dy6RJkxgxYgRPPPEEGRkZAAwYMIAXX3yx6VouIiINYxhQXHyie9h27vXUI9hT\njlyPh2xRYb278Dp5d94+VAYGUtmuHZXdulcFp/+JI9iqo9VAjMCg00IWLy8wmZruZ+Hg6g3nxMRE\nYmNjAYiKiiIvL4+CggJ8fX2prKxkw4YNzJ8/H4D4+HgA0tPTm7DJIiLnsJO7h23nXnOrn3vNO+kc\n7MmBm5fb8O5h/2Pdw52jT+8ePha2xwM1sGMY2ZVu9XYPS/3qDefMzEx69OhhmzabzVitVnx9fcnO\nzsbHx4enn36a5ORk+vfvz/333w/Azp07ueOOO8jLy2P69OkMHjy46aoQEWlJysqOXSmcc9pVw6cd\nwR6btr1uaPewm9uJLt/27auFamVg0OnnXk9+7effsO5hix8VzXRO1tk1+IIw46T/FIZhcOjQISZO\nnEhYWBi33XYba9asoVu3bkyfPp0rrriC9PR0Jk6cyKpVq/Dw8Kh1u0FB3ri5uZ5dFY3EYvGz6/6b\nmrPXB85fo+pzEIYBJSWQk1P9X25u7dO5uViOvy6sv3u4Gh8fCAyEiHAIOq/qdVDQia/H/508fey1\nydsbk8nUbA+1aDHv4VlqrvrqDeeQkBAyMzNt04cPH8ZisQAQFBREu3btiIyMBGDgwIHs2LGDoUOH\nMnr0aAAiIyNp3bo1hw4dIiIiotb95OQ07FL3xmax+GF14r/4nL0+cP4aVV8jq6zEVJBfx9XDOad3\nC598m05p6RnvyjCZMAUEUOEfQGWnzqefez3paLX696q6kanjwKZORZVQVHB2654F/R9t+PZqU284\nDx48mJdeeolx48aRnJxMSEgIvr6+VSu7uREREcGePXvo0KEDycnJjBkzhmXLlmG1Wpk8eTJWq5Ws\nrCxCQ0MbrSAREeBE9/CR3FrOvZ4UrKecjzUdOYKpsvKMd2XrHvYPwIiIOClcg6pdKVzjbTr+AVhC\nA8h24uCSxlVvOPft25cePXowbtw4TCYT8fHxLF26FD8/P0aMGEFcXByzZs3CMAy6dOnC8OHDKSoq\n4oEHHuDrr7+mrKyM2bNn19mlLSLnsGNXD2NNx23X/qrzsKecc3XJO+VBE8fPwxY27KjQ8PamMiCQ\nyjZtMWK61XHfa9BJVxIfu3rY2/ucvnpYmpfJMBpwZUETsndXiLpjWj5nr9Fh6zOMqquH80659cZ2\nBJtTPVxPvV3n6NEG7a7ypKuDq9/3GlDLfa9BtnXOunu4ETjs+9eInL1Gh+rWFpFzQHn5iauHa3xy\n0+lXENu6h/PyGt49fPyo9KTu4VZtQijy8LaFa7Vzr8cfLuHnD672vXBUpDkonEWcRUnJKQ/0z6n+\nQP9TLmiq1j1c0LCjAcPLq6p7OCQUIzqm1vteq4XrsUDGx6fG7uFWFj8KnfioS6QhFM4ijsIwqq4e\nPrV7+FiAUlaEb8ah2p/i1NDuYT9/jMBAKjp0pLy27uHAwOpPcTrePezp2UQ/BBEBhbNI46qoOH3I\nuVNv07EdweacOHI9vkxFRZ2br/ZoRFdXW4iWh4Udu7Cplltzjr8+6eph3PTrL+Ko9NspcqqSkpMC\ns5axX0+9sOl4yOYfadCujFatqrqHW1swoqJreOZwoO0pTgHt25JteJy4eriW7mERafkUzuJ8DANT\nYUEtg6nn1P2IxLxcTCUlDdpdpa9fVWBGRFJe07nXaoEbVK2rmFatznxHejSiyDlD4SyOqaLixPnU\nUwdTP+17VUPXkX+E4OzsM+oePpnh6lp1641/AOVt257ePXzyPbCnHNWqe1hEmoI+VaTpHD160lFq\nLd3DJz8O8eSH/ze0e9jTE4KCTnQPVwvUAIyAoFovdjJ8/dQ9LCIOReEstTMMKCysZbScnJpvzTn5\nIqg/2j18ykMlqt/3GlR97NdWrbBY/MhRt6+IOAGFs7M71j3MkcO47d5/yiMQTz6CreHca14epvLy\nM96V4eJi6+qtuXv4lCc3He8ePvZa3cMiIlX0adgSlJaedBtOTvUB1k+9sOnU23fyj9jGfg06g10Z\nHh5VoWoOxugYVb17ODAQw7/6E5tODlx1D4uINA6Fc3MwDCgqOv2ZwycHbU1D0h1ftqhhw2lW+vhW\nBWd4hC1cPdtYKPL0ruFBE6d0D3t51b8DERFpUgrnM1VZWfvVw7V1Dx9fNi8PU1nZGe/KMJlsD/Qv\nj445cRtObY9ItN2aE1Rr97BFj0YUEWkxzq1wLi09KUhzqj1zmPJifPYfqvXq4ZO7h8+ErXs4yIzR\nvmP1e12PjwF7ypB01bqHXVya8AchIiKOzCnD2WPVF7R6563TQ7ae7mHvU6Zt3cNh4TWE6ylPcTp2\nLvb4IxLx8tL5VxEROStOGs4r8Vz5RfXu4c5dTnuoxMndw/7t25GDx4mgDQgAd3d7lyIiIucgpwzn\ngn8+R2H83zB8fM+8e9jiR7nOyYqIiANwynDGZKoalF1ERKQF0lVHIiIiDkbhLCIi4mAUziIiIg5G\n4SwiIuJgFM4iIiIORuEsIiLiYBTOIiIiDkbhLCIi4mAUziIiIg5G4SwiIuJgFM4iIiIOxmQYDRik\nWERERJqcjpxFREQcjMJZRETEwSicRUREHIzCWURExMEonEVERByMwllERMTBuNm7AU1pzpw5JCUl\nYTKZiIuLo1evXrZ5ixcvZtmyZbi4uNCzZ08eeeQRysvLeeSRR9i7dy8VFRU89NBD9O/fnxtvvJGi\noiK8vb0BmDlzJj179rRXWTYNrW/p0qW88MILREZGAjBo0CDuvPNOtm3bxuzZswGIiYnhiSeesEc5\np2lofa+99hpr164FoLKykszMTFauXMnw4cNp06YNrq6uAMybN4/Q0FC71HSqumr86quveO211/Dw\n8GDMmDFMmDCh1nUOHDjAQw89REVFBRaLhX/+8594eHjYqyybs6nvmWeeYcOGDZSXl3P77bdz+eWX\nM2vWLJKTkwkMDARg8uTJDB061B4lVdPQ+tatW8eMGTOIjo4GoEuXLjz22GNO8/599NFHLFu2zLbM\nli1b2LRpk8N+hgKkpKQwdepUbr75Ztv/wePWrl3L/PnzcXV1ZciQIUybNg1opt9Bw0mtW7fOuO22\n2wzDMIydO3ca119/vW1efn6+MWzYMKOsrMwwDMO45ZZbjE2bNhlLliwx4uPjDcMwjJSUFOO6664z\nDMMwJkyYYGzfvr15C6jH2dT38ccfG3Pnzj1tWxMmTDCSkpIMwzCM++67z1izZk0zVFC3s6nvZEuX\nLjUWLlxoGIZhDBs2zCgoKGimlp+5umqsqKgwhgwZYmRlZRkVFRXGpEmTjAMHDtS6zqxZs4zPP//c\nMAzDePbZZ43Fixc3czWnO5v6EhMTjSlTphiGYRjZ2dnGpZdeahiGYcycOdP45ptvmr2GupxNfT/9\n9JNx1113nbYtZ3n/Tl1/9uzZhmE45meoYRhGYWGhMWHCBOPRRx813nnnndPmX3HFFUZGRoZRUVFh\njB8/3tixY0ez/Q46bbd2YmIisbGxAERFRZGXl0dBQQEA7u7uuLu7U1RURHl5OcXFxQQEBHDVVVfx\n8MMPA2A2m8nNzbVb++tzNvXVpLS0lP3799v+Ih42bBiJiYnNU0Qd/kh95eXlvP/++6f9Fexo6qox\nJycHf39/zGYzLi4uXHTRRaxdu7bWddatW8dll10GtIz3sLb6LrjgAl544QUA/P39KS4upqKiwm41\n1OVs6quNs7x/J3vllVeYOnVqs7e7ITw8PFi4cCEhISGnzUtPTycgIIC2bdvi4uLCpZdeSmJiYrP9\nDjptOGdmZhIUFGSbNpvNWK1WADw9PZk2bRqxsbEMGzaM3r1707FjR9zd3fH09ATg7bff5k9/+pNt\n/RdffJEbbriBxx9/nJKSkuYtpgZnUx/A+vXrmTx5MjfddBNbt261/ZIdFxwcbNuOPZ1tfQCrVq3i\n4osvplWrVrbvxcfHM378eObNm4fhIA/Fq6tGs9lMYWEhe/bsoaysjHXr1pGZmVnrOsXFxbYutJbw\nHtZWn6urq63rc8mSJQwZMsR2OuLdd99l4sSJ3HvvvWRnZzd/Qac4m/oAdu7cyR133MH48eP58ccf\nAZzm/Tvut99+o23btlgsFtv3HO0zFMDNza3a58TJrFYrZrPZNn28/ub6HXTqc84nO/kDuaCggAUL\nFrBixQp8fX256aab2LZtG127dgWqzmcmJyfz+uuvAzBx4kRiYmKIjIwkPj6exYsXM3nyZLvUUZsz\nqa93796YzWaGDh3Kpk2bmDlzJm+++Wat23EkDXn/Pv7442rnze+++24uueQSAgICmDZtGitXrmTU\nqFHNXkN9Tq7RZDIxd+5c4uLi8PPzIzw8vN516vqeI2hIfV999RVLlizhX//6FwB//vOfCQwMpFu3\nbrzxxhu8/PLLPP74483a/vqcSX0dOnRg+vTpXHHFFaSnpzNx4kRWrVpV63YcSUPevyVLlnDNNdfY\nplvCZ+jZaqrfQac9cg4JCan2l9zhw4dtf8WlpqYSERGB2WzGw8OD/v37s2XLFgA++ugjvvnmG159\n9VXc3d0BGDFihO0iquHDh5OSktLM1ZzubOqLioqyXUTTp08fsrOzCQoKqtZ9f+jQoRq7eJrb2b5/\nRUVFHDx4sNqHxdVXXxbN9R8AAAMrSURBVE1wcDBubm4MGTLEId4/qLtGgAEDBvDee++xYMEC/Pz8\nCAsLq3Udb29v29FIS3gPoeb6AL7//ntef/11Fi5ciJ+fHwADBw6kW7duQMv4HYSa6wsNDWX06NGY\nTCYiIyNp3bo1hw4dcqr3D6q66fv06WObdsTP0PqcWv/x96W5fgedNpwHDx7MypUrAUhOTiYkJARf\nX18AwsLCSE1Ntf0gt2zZQocOHUhPT+eDDz7g5ZdftnVvG4bBzTffzJEjR4Cq/3THr7S0p7Opb+HC\nhSxfvhyoukLxeLh16tSJX375BajqEr7kkkvsUFF1Z1MfwLZt2+jUqZNtO/n5+UyePJnS0lIAfv75\nZ4d4/6DuGgGmTJlCVlYWRUVFrF69moEDB9a6zqBBg2zfbwnvIdRcX35+Ps888wwLFiywXZkNcNdd\nd5Geng60jN9BqLm+ZcuWsWjRIqCq2zQrK4vQ0FCnef+gKph8fHxsXbyO+hlan/DwcAoKCti3bx//\n3979uioMxVEAPxcFuYLJMBj+AWIRs0EQZvSPMBv9kdQkYzhEEJsGmxaxKCiCzaJRTCZBEKNYxKEv\nCAPh8cDi9sb59A0O4+6M7+6YZVlYLpdIJpNfW4Oe/iuVaZrYbDYQQqBWq2G32yEUCkHTNAwGA4xG\nI/h8PiQSCZRKJTSbTUwmE6iqap+j1+thsVig2+1CSglFUVCv1yGldDDZy6f5TqcTisUins8nLMuy\nPwHY7/eoVqt4PB6Ix+P2pjinfZoPAGazGVar1dtYu9/vYzweIxAIIBaLoVKpQAjhVKw3f2Wcz+fo\ndDoQQiCXyyGbzf56TDQaxfl8Rrlcxu12g6qq0HXdnvw46dN8w+EQ7Xb7bQ+BYRg4HA5oNBqQUiIY\nDELXdYTDYQeTvXya73q9olAo4HK54H6/I5/PI5VKeeb6Aa+H5Var9fbKbDqduvIeut1uYRgGjscj\n/H4/FEVBOp1GJBKBpmlYr9cwTRMAkMlk7FH8N9agp8uZiIjoP/LsWJuIiOi/YjkTERG5DMuZiIjI\nZVjORERELsNyJiIichmWMxERkcuwnImIiFyG5UxEROQyP9yTNc9YIOnoAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jgmH3wwt1src",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Okay, so we are doing good!
\n",
+ "\n",
+ "Now, let me just put everything here into one function so that you can tweak the hyperparameters easily!\n",
+ "\n",
+ "Or better, do it yourself!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "OZ5TY7B_4E_v",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "def linear_regression(learning_rate=0.000005, n_epochs=100, interval=50):\n",
+ " # YOUR CODE HERE\n",
+ " optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)\n",
+ " \n",
+ " with tf.Session() as sess:\n",
+ " # We need to initialize the variables in our graph\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ "\n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ "\n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ "\n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ "\n",
+ "\n",
+ " print ('The final loss is: ', final_loss)\n",
+ "\n",
+ " # Plotting the final predictions against the true predictions\n",
+ " plt.plot(test_X, test_Y, 'g', label='True Function')\n",
+ " plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "A6MaclhK4rc6",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 563
+ },
+ "outputId": "b7b73c64-d321-465d-8948-6efd9580147e"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Okay! Now let's tweak!\n",
+ "linear_regression(learning_rate=0.000034, n_epochs=500)"
+ ],
+ "execution_count": 24,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.07932834\n",
+ "Loss after epoch 50 is 0.07910691\n",
+ "Loss after epoch 100 is 0.07888704\n",
+ "Loss after epoch 150 is 0.078668706\n",
+ "Loss after epoch 200 is 0.078451835\n",
+ "Loss after epoch 250 is 0.07823657\n",
+ "Loss after epoch 300 is 0.0780227\n",
+ "Loss after epoch 350 is 0.07781037\n",
+ "Loss after epoch 400 is 0.077599496\n",
+ "Loss after epoch 450 is 0.077390045\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.07722866\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAecAAAFKCAYAAAAnj5dkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3XlcVXX+x/HXZVV2Ll5QEVxQXDAN\nNTfK1LAyp6mZadEyK23M1LLFSaMFm9KcRp2y1RybmsaKqew3tqlj6bRImkukmBsq4IYgO8h+fn+g\nV1FWBe7l+n4+Hjy4595zzv1+uMLb8z3ne74mwzAMRERExG442boBIiIiUpXCWURExM4onEVEROyM\nwllERMTOKJxFRETsjMJZRETEzrjYugGnpafn2fT9/f09yMoqtGkbmpKj1weOX6Pqa9kcvT5w/Bob\nuz6LxbvG13TkfIqLi7Otm9CkHL0+cPwaVV/L5uj1gePX2Jz1KZxFRETsjMJZRETEziicRURE7IzC\nWURExM4onEVEROyMwllERMTOKJxFRETsjN3chMQevfLK39i9+1cyM09QVFRE+/bB+Pj4Mm/eXxtl\n/7fcciOBgUE4OZ35P9Krr7510fv9/vv/MWjQUHJzc1i2bAmPP/7kRe9TRESaT73Cec+ePUydOpV7\n7rmH8ePHV3ltw4YNLFq0CGdnZ4YNG8a0adMAmDdvHgkJCZhMJmJiYujTp0/jt76JPfjgIwB8+eVn\n7N+fxPTpDzf6eyxYsBgPD49G3eeHHy6nX78rCAhoo2AWEWmB6gznwsJCnnvuOYYMGVLt688//zzL\nli0jKCiI8ePHc91115GZmUlycjJxcXEkJSURExNDXFxcozfeVrZu3cyHH/6LwsJCpk9/hMcem84X\nX3wNwFNPPc7vf38bPXr0ZN68Z8nLy6O8vJyHH/4TXbt2q9f+x4y55rz9bdu2hYKCfFJSkjl8+BAP\nPfQYQ4ZEsWrVF3z8cRwmk4mxY++ktLSUnTt3MHPmQ8ye/TTPPvsUy5a9x8aNG3nxxQW4uLhgsQTy\nxBPPsHbtan755Weys7NISUnmjjvu4je/ubnJfm4iIlI/dYazm5sbS5cuZenSpee9lpqaiq+vL+3a\ntQPg6quvJj4+nszMTKKjowEICwsjJyeH/Px8vLy8LrihczY8xWdJ/3fB21fnxrCbmTP0+QvaNilp\nHx98sAI3N7dqX//3vz9g0KCh3HjjzRw4sJ+XX17ASy+9fjHN5fjxNBYsWMyPP27gP//5hL59L+ed\nd/7Ou+9+QElJKXPnxjJ//iL+/vc3WbBgMTk52dZtY2NjWbDgFYKC2rJo0V/4739XYTKZSErax5tv\nvs2hQ6nExsYonEXkklNSXsKKvR/h6uRKmF9XuviG4ePua9M21RnOLi4uuLhUv1p6ejpms9m6bDab\nSU1NJSsri4iIiCrPp6en1xrO/v4etd631KO1G05Oprqa2yAerd2q3Hi8ppuQe3u3wsPjzLp+fh70\n6tWT4OAAAEwmk/U1d3dX/Pw82L07kczMTNatWwNAcfHJ8/bv7OzEE088grNzZd3+/v4sXry42v15\nerozZMggLBZvunfvTHHxSXJyjtOtW1c6dLAAsGzZUut+27Txwtm5FBcXJ1xdyzGZTPTuXXnkPnz4\nVfz000/06tWLK67oT9u2fnh7u3LyZEGtN2JvCVp6++ui+lo2R68PWl6Naflp3P7vP/BD6g9Vng/y\nDCI8ILzK1wjvEVgszRPazXJBmGEYda5T10wfj0c+w+ORzzRWk6xOz4ZlsXjXODNWXl4RhYUl1tez\nswsxDJN12TAM6+OCgpPW1x988DF69z5zrv3c/ZeXV/DCC3+rcs45PT2v2v0VFBTj6tqa9PQ8srIK\nKCkpIyeniKKikmr3m5GRT05OAWVlFZw4UVBlnydO5FJUVEZeXhElJRWkp+dRWFhIeXmFzWcHuxi1\nfYaOQPW1bI5eH7S8Gn9J/5m7v7qDw/mH+G3Y7xjSPor92ftIytlHUvY+fkj9ge9SvrOuP6bbGP4x\n6oNGe//a/iNzUeEcGBhIRkaGdTktLY3AwEBcXV2rPH/8+HEsFsvFvJVdM5lMFBUVAbBnz24AevXq\nzbffrqd37z4cOLCfjRs3MHbs+Np2U+v+qtOxYydSUpIpLCzE2dmZWbMe4W9/ew2TyYny8nLrej4+\nPphMJo4dO0bbtm35+eet9OlzeZV1REQuJf+39xNmrJtKUVkRMYOeYUa/xzCZqvbOFpcXk5xzkKSc\nfezPTuL6Xtc0W/suKpw7dOhAfn4+hw4dom3btqxbt44FCxaQlZXFK6+8wtixY0lMTCQwMPCizjfb\nu5tvvoXJk++mU6cudO/eE4BbbrmduXPnMHXqfVRUVPDwwzMvan/Vad26NZMmTeHhh6cCcPvtd2Ay\nmYiM7MfUqZN48sk51nWfe+45nn32SZydnQkO7sA111zLmjVfXVjBIiItVIVRwQsbn+PlrQvxcvXm\nnzd8yHWdRle7rruzO+Hm7oSbuwPN2zNgMuroc96xYwd/+ctfOHz4MC4uLgQFBTFy5Eg6dOjAqFGj\n+Omnn1iwYAEA1157LZMmTQJgwYIFbN68GZPJRGxsLD169Ki1IbbuCmlp3TEN5ej1gePXqPpaNkev\nD+y/xrySXB74732sSV5FZ98u/HP0h3Q3155NZ2vs+mrr1q4znJuLrT9Qe/9HdbEcvT5w/BpVX8vm\n6PWBfde4P3sfE74ax56s3QwPGclbo/6BXyv/Bu2jOcNZdwgTEZEWqbS8lI3H4llzcBUHc/ZjYFgv\nQD792KByeXPaT+QUZzOl73SeGfJnXJzsO/7su3UiIiJnySw6wTcpa1lz8Cu+Sfma3JKcem3n4eLJ\nKyPf5PYedzRxCxuHwllEROzavqy9rDr4JWsOfsWmYz9SYVQAEOIdyq3db2dUx+uJDOyHs8kZk8mE\niVNXXZ/12M3JDVdnV1uV0GAKZxERsSuGYfBL+s98eeAzvtj/GXuyKoeUmjDRP+gKrus0mlGdrqen\nudd5w58chcJZRERsrryinE3HfuTL/ZWBfCg/FYBWzq0Y3fk3jO48hmtCr8Xi4bj3zDibwrkWR48e\nYcKEsXTvXnmpfUlJCXfeeTdXXz2iwfv65JM4srOzGTZsON9+u55Jk+6vdr3T0z26utbd/bJ//z4W\nLXrxvGkmr756EJdd1te6HBAQwOuvv9rgNp9r3bq1jBgRzd69u2utQUSkPo7mH+HHoxv47tD/WHXw\nCzJOVt68ytvNhz90u40xXX7LiNBr8HT1tHFLm5/CuQ6hoR2t4Zebm8O9997J4MFDcHdvdUH769at\nO926da/x9dPTPdYnnGvi5eXVKPNCn+tf/3qXESOi66xBRORchmFwICeJ+CMb+PFo5Vdy7kHr621a\nW7ir172M6XIjVwYPw825+kmFLhUK5wbw8fElIKANJ06c4B//WIqLiyu5udn8+c/zefHFuRw5cpiy\nsjLuu28K/ftfwebNm1i8eCFmcwABAW1o3z6YrVs3s2LFv3n++Rdrne7x5ZffYOXKT1m7dhUmkxNX\nXTWccePGc/x4Gk8/PRtXV1e6dg2vd9sPHTrE1KnTWbbsPQAmTbqL55//C2+//RZt2ljYvftX0tKO\n8cwzz9O9ew+WL3+X9eu/xmRyYsqU6ezatZN9+/YQE/MnbrnldmsNX3/9X+LiluPs7Ez37j15+OGZ\nLFu2pNrpLUXk0vNNylre//U9fjy6geOFadbnfd39uLbj9QxuH8XgdkOIDOyPs1PNkx9dalpMOHvO\neQr3zxp3ysjiG2+mYE79p4w8evQIubk5BAYGAZX3rJ4160lWrfqCgIA2PPHEM2RnZzNjxhTeffdD\nlix5laeffo5u3cKZOfMh2rcPtu6rsLCg1uke09OPs37917z++jIAHnhgEiNGRLNiRRzXXHMtt902\njn/96x327dtz0T+HkpISFi16lf/7v49ZteoLPDw8WL/+a5YseYcjRw7zr3+9w+zZT7N8+bvMm/dX\ntm7dfKqGQt566zX+8Y/38fDw4PHHH7G+du70lgpnkUtLSm4yT/0wm1UHvgAgyKMtN3f9PYPaDWVI\n+yh6mHviZHKycSvtV4sJZ1tJSUlm+vTJQOXc1k899ax1Cs1evSqnxdyx4xcSErbxyy8/A1BcXExp\naSlHjx6lW7fKo9vLL+9HcXGxdb8HDx4gNLQT7u6tcHdvxfz5i6q876+/JnLoUCoPPlh5XrewsIBj\nx45w8OABRoyonCs7MnIAP/644bw25+fnW9sMEBbWlalTaz4/3LdvJAAWSxA7dyayZ89uevXqjZOT\nEx06hDB79tPVbpeamkKHDqHWWbUiI/uzZ88uAPr0uRyonBwlPz+/xvcWEcdSVFbEq9teYvHWRRSV\nFzG43VCei3qBPpbLHfbK6qbQYsK5YM7zDTrKbSxnn3M+l4uLq/X7hAkTGTXq+iqvOzmd+V/huXdJ\ndXJyxjg1Vq+mfQ8ZEsXjjz9Z5fnly9/FdOp/mzVtX90555KS3CrLZWVl1sen55M+3U5nZycqKuq+\nq6vJVLWusrJS3N3dq92niDi+z3Z/xoNfPkRy7kECPYJYNPQV/tDtNoXyBVCfQiPo1as333//PwCy\nsjJZsuQ1ANq0sZCSchDDMNi2bUuVbc6e7rG4uJiHH56KYRjW6R67d+/J1q1bKCoqwjAMXnppAcXF\nRYSGdmTXrp0A1i7k+vDy8iIrKxPDMDhxIoMjRw7VuG737j3Zvj2BsrIyMjNP8MQTlTNqnRvYISEd\nOXQohcLCAgC2bdtK9+696t0mEXEM+3OSuPOLW/nth7/lcP4hHuj7IPF3bOGW8NsVzBeoxRw527OR\nI6PZuvUnpkyZSHl5ORMnVnYpT548laeemkXbtu2s56lPq2u6x1deeYvbbhvHtGl/xMnJiWHDhuPu\n3opbbx3H00/P5ttv1xEW1q3ebfT19WXAgIHcd98EunbtVuvV1u3atee6625g+vTJGIbB/fdPAyA8\nvDt//OMEHnjgIWsN06bN4LHHHsRkcqJPn8vp2/dyNm/e2KCfn4i0TOmF6byZ8CpLEl6jpKKEkZ1H\n8uyg+Q2a6Umqp1mpTrHn2VQag6PXB45fo+pr2RypvtS8FF7/eTHv//oeJ8tO0s6zPX+OmsekwRPI\nyHDca0w0K5WIiNidXZm/8srWv7Fi70eUG+WEeIcy9fKHGNdjPB6uHurCbkQKZxERqdXmY5tYvHUR\nqw5+CUB3/x482O8Rftf1lhY1mURLonAWEZEqSspL+Pn4NuKPfM/alDVsPBoPQP+gK5jR7zGu7XS9\nxig3MYWziMglrri8mK1pm9lw5Hs2HPmBzcc2crLspPX14SEjmdHvMYa2v1Jd181E4Swi4qDKK8o5\nVnCUzOJMsooqvzKLqj4+nH+IrWmbKSovsm7X09yLIe2jGNr+Sga3jyLQI9CGVVyaFM4iIg6ktLyU\n7w7/jy/2r+TL/Z9xouhEreubMNEroDdRwVcypP2VDG43lIDWAc3UWqmJwllEpIUrLi/mf6nf8FnS\nf1h98Euyi7MBsLQO5Oauv6dNawv+rcyYW5nxb2XG3/3M44DWbS7JKRntncJZRKSFWpfyNf/e/QFr\nkleRd+oWve0823Nr+Fh+E3YTA9sO1kxPLZTCWUSkhSkoLeDJ7x7n/V2VU8CGeIcyvufd/Cbst/QP\nukJXUjsAhbOISAuyI2M796+5l73Ze7isTV9evHoR/QIH6CpqB6NwFhFpAQzD4O0dS5mz4UmKy4u5\nv89UnhryLO7O7rZumjQBhbOIiJ3LKsrk4XXT+erA55hbmVl23T+5ttNoWzdLmlC9wnnevHkkJCRg\nMpmIiYmhT58+1tfWrl3LG2+8gZubG2PGjGH8+PFs3LiRGTNm0K1b5axJ4eHhPP30001TgYiIA/vx\naDwP/HcSh/MPEdX+Kl6PXko7r/a2bpY0sTrDedOmTSQnJxMXF0dSUhIxMTHExcUBUFFRwXPPPcen\nn36Kn58ff/zjH4mOjgZg4MCBLF68uGlbLyLigIrLizmQs5+V+z5l0ZYXAZg98Clm9HtMV19fIuoM\n5/j4eGvghoWFkZOTQ35+Pl5eXmRlZeHj44PZbAZg8ODBbNiwgeDg4KZttYhIC1dhVHA4/xBJ2ftI\nyt576vs+knKSSM1NxqByNt9grw68MWoZg9sNsXGLpTnVGc4ZGRlERERYl81mM+np6Xh5eWE2myko\nKODgwYMEBwezceNGBg4cSHBwMPv27WPKlCnk5OQwffp0oqKimrQQERF7VVZRRuLxRNbv+YHt6Qls\nz/iF7Rm/WMcmny3QI4jB7YcS5tuVbv7dGdvjDvxbmW3QarGlBl8QZhiG9bHJZGL+/PnExMTg7e1N\nhw4dAOjUqRPTp09n9OjRpKamMmHCBNasWYObm1uN+/X398DFxbbdNbVNfO0IHL0+cPwaVV/LkF6Q\nzqp9q4g/FM/Wo1tJSEugqOzMvatNmOjepjt9g0bTo00PwgPCrV8+7j42bPnFc5TPsCbNVV+d4RwY\nGEhGRoZ1+fjx41gsFuvywIEDef/99wFYuHAhwcHBBAUFccMNNwAQGhpKmzZtSEtLIyQkpMb3ycoq\nvOAiGoPF4k16ep5N29CUHL0+cPwaVZ/9MgyD7RkJ/Dd5NWuTV7M1bYu1W9rFyYUe5l5c0aE/4d69\nuKzN5fRqE4GXq9d5+ynOhXRa5s8AWvZnWB+NXV9tQV9nOEdFRfHKK68wduxYEhMTCQwMxMvrzD+q\n++67j7/85S+0bt2adevWce+997Jy5UrS09OZNGkS6enpnDhxgqCgoMapRkTEDuSX5vNt6nrWJq/m\nv8mrSSs8BoCzyZnB7YcS3fE6hgVfTY+AXrg7uzt8cEnjqjOc+/XrR0REBGPHjsVkMhEbG8uKFSvw\n9vZm1KhR3HbbbUycOBGTycTkyZMxm82MHDmSmTNn8vXXX1NaWsqcOXNq7dIWEWkp9ucksSThNT7c\ntdw653FAqwBuDR/LqI7XMTxkJH6t/G3cSmnpTMbZJ5FtyNb/o3T0/9U6en3g+DWqPtvadHQjr/+8\nmK8OfI6BQah3R24Jv43ojtcRGdi/ziFO9l5fY3D0Gu2qW1tE5FJVXlHOlwc+5/WfF7Ml7ScAIgP7\nMfXyhxjT5be4OOlPqDQN/csSETnHsYKjfJ70H5b88jrJuQcBuL7TDTxw+YMMbjdUk0xIk1M4i4jD\n2XkikbySPEK8QwjyaFtnl3NKbjLxR36o/Dr6Awdy9gPg7uzOhF4TmdJ3Gl39uzVH00UAhbOIOJCj\n+Ud4Nv4pVuz92Pqcq5MrwV4dCPHpSKh3KCGnvorLi62BfCg/1bq+t5sPozpex9D2V3Fb93FYPCzV\nvZVIk1I4i0iLV1JewpJfXmfhT3+hsKyAyy2RXNnhag7lpZCal0JKbgrfHVpf7bbmVmZu6HwjQ9oP\nZWj7K+kV0Fv3rxabUziLSIv2Tcpanvz+cZKy9xHQKoDnr5zPHT3vwsnkVGW9wtJCDucfIjUvmZTc\nFAAGtRtCd3OP89YVsTWFs4i0SCm5yTz9wxN8deBznExOTLpsMrOueLLGMcYerh508w+nm394M7dU\npOEUziLSoqQXpvOPHUt5ddtLFJUXMajdEF64agG921xm66aJNBqFs4jYvcLSQlYf/JKPdn/IutSv\nKTfKCfJoy9+GPs/vu92qoU3icBTOImKXyivK+f7wt3y8J47P96+koDQfgMstkdwSfjt39LwLLzfH\nngFJLl0KZxGxKwdy9vNu4tus2PsRxwqOAhDiHcrkPlP4Q7fbCTd3t3ELRZqewllE7MKujF08s/ZZ\nPtn7byqMCnzd/bir173cGn47A9sN1hXVcklROIuITf16Yid/2/Ii/9n3KQYGPc29mNH/MW7ofCOt\nXFrZunkiNqFwFhGb2J6ewKItf+WL/SsBiGwbyUOXz2R05zE6SpZLnsJZRJpNhVHBxqPxvLbtZdYk\nrwKgX2B/Hh3wOHcMuJWMjHwbt1DEPiicRaRJVRgVbD72EyuTVrAy6f+sF3kNbDuYxwbMYnjISEwm\nk4ZDiZxF4Swijc4wDLYe38x/9n3KZ0n/x+H8QwD4uftxR4+7uK37OIa0j1Igi9RA4SwiFy2rKJO9\nWXvZl72HnSd28NWBL0jNq7x/tY+bL7d3v4Obuv6OYR1G4ObsZuPWitg/hbOI1FtJeQkbjnzP7sxf\n2Zu1l73Zu9mbtYeMk+lV1vNy9eaW8Nu5uevvuTpkJO7O7jZqsUjLpHAWkToVlBbwr53v8MbPr3Kk\n4LD1eRMmQn06EhnYj65+lZNKdPUP53JLpIZBiVwEhbOI1CirKJNl29/i79vfJLMoEw8XDyZdNpnB\n7YbSzb87XXzDFMIiTUDhLCLnOZp/hDcSXuWfif+gsKwAP3c/Zg6YzaTL7iegdYCtmyfi8BTOImK1\nP3sfr257mX/v/oCSihLaerZj1sAnuSviHrxcvWzdPJFLhsJZREjM2MHirQv5T9KnVBgVdPbtwoOR\nj3Br97G6mEvEBhTOIpewzcc28fLWhaw++BUAEQGXMaPfo9wYdjPOTs42bp3IpUvhLHKJMQyD7w7/\nj5e2LOD7w98CcEXbQTzSfybXhF6rG4OI2IF6hfO8efNISEjAZDIRExNDnz59rK+tXbuWN954Azc3\nN8aMGcP48ePr3EZEml9m0Qn+l7qOJQmvsfX4FgCGh4zk4X4zdbcuETtTZzhv2rSJ5ORk4uLiSEpK\nIiYmhri4OAAqKip47rnn+PTTT/Hz8+OPf/wj0dHRpKSk1LiNiDSP3OIc4o9u4PvD3/L9oW9JPLHd\n+toNnW9kRr9HiQzqb8MWikhN6gzn+Ph4oqOjAQgLCyMnJ4f8/Hy8vLzIysrCx8cHs9kMwODBg9mw\nYQOpqak1biMiF6asooztGb9QVl5KuVFOhWFQQQUVFeWV340KCksL+enYRr4//D8S0n+mwqgAwN3Z\nnSuDh3Fl8DDGdPkt3c09bFyNiNSmznDOyMggIiLCumw2m0lPT8fLywuz2UxBQQEHDx4kODiYjRs3\nMnDgwFq3EZGG23R0I7M/foQdx3fUa30XJxeuaDuIqOCruCr4avoHXaGbhYi0IA2+IMwwDOtjk8nE\n/PnziYmJwdvbmw4dOtS5TU38/T1wcbHt1aEWi7dN37+pOXp94Hg1Zp3MYvba2by19S0Abo+4nRCf\nEJxMTjg7OVd+N1V+dzI54ersSr92/YgKicLTzdPGrW84R/v8zuXo9YHj19hc9dUZzoGBgWRkZFiX\njx8/jsVisS4PHDiQ999/H4CFCxcSHBxMcXFxrdtUJyursMGNb0wWizfp6Xk2bUNTcvT6wLFqNAyD\nT/b+m2d+iCHjZDo9zb1YetNbhLeu34WVhTkVFNKyfhaO9PlVx9HrA8evsbHrqy3oneraOCoqitWr\nVwOQmJhIYGBgle7p++67jxMnTlBYWMi6desYMmRInduISM32Z+/j1s9uZuraP1JQms9Tg59l7a3f\nERUaZeumiUgzqfPIuV+/fkRERDB27FhMJhOxsbGsWLECb29vRo0axW233cbEiRMxmUxMnjwZs9mM\n2Ww+bxsRqV1xeTGvbnuJl7YsoLi8mOjQa3lh2AI6+nSyddNEpJmZjPqcEG4Gtu4KUXdMy9cSa8wv\nyWNd6jesOfgVX6esIeNkBkEebZl31Yv8pstNVcYet8T6GkL1tXyOXmNzdmvrDmEizSwlN5n/Jq9i\n9cGv2HD4e0oqSgAI9Ajigb4P8tiAx/Fx97VxK0XElhTOIk2gpLyEtMJjHM0/SlrhUY7mHyE1P5Vv\nU9fxa+ZO63qXtenLtZ2u59qO19M3MBInU52XgYjIJUDhLHKRyirK+GL/Sj7Z+xGH8lI5VnCUjJPp\n1a7r7uxOdOi1XNtpNNd2up72XsHN3FoRaQkUziIXqLC0kA93L+eNn18hOfcgAB4uHrT1bEd3/x4E\nebalnWd72nm2o61nO9p6tieiTW88XVve+GMRaV4KZ5EGyiw6wdvbl7Js+xJOFJ3A3dmdCb0mMqXv\nNML8umoCCRG5aApnkXpKyU1mScJrLP/1nxSWFeLr7scj/Wcy6bIpBHoE2rp5IuJAFM4iNcgqymRL\n2k/8dGwjPx3bRPyRHyg3ygn26sATfZ/mzp4T8HJz7FsViohtKJxFgAqjgqTsfaeCuPJrT9buKuv0\ntUQyuc8D3Nz1D7g6u9qopSJyKVA4i8P78Wg8/0x8mxMnMzhZdvLUVyFFZUUUlhVal09Prwjg6erF\nVR2Gc0XbgQxsO4h+gQPwa+VvwypE5FKicBaHZBgG3x/+lkWbX+SHI99ZnzdhorVL61NfHvi7+9PO\nsz2tXFoR6t2Rge0GM6DtQHqae+HipF8PEbEN/fURh2IYBt+k/JdFW/7KT8c2AjAyNJqH+/+Jyy2R\nuDu762pqEbF7CmdxCIZh8J9d/2HON8/yc/o2AK7vPIZH+s0kMqi/jVsnItIwCmdp0QzD4KsDX/Di\nT/PYeWIHJkz8Nux3PNx/Jr3bXGbr5omIXBCFs7RYPxz+jud/jGVL2macTE7cedmdTImYQXdzD1s3\nTUTkoiicpcVJOL6NuRufZX3qNwDcGHYzswc+xdDw/g49XZ2IXDoUztJiJGXvZf7GufwnaQUAwzqM\n4MlBz+icsog4HIWz2L3UvBRe2rKQ93/9J+VGOZGB/Xhy8ByGdRhu66aJiDQJhbPYpbySXD5PWslH\nez7kh8PfYWDQzS+cJwY9w5guN2o4lIg4NIWz2I3S8lLWp37NR3s+ZNWBLykqLwJgULsh3NlzAreE\n364bg4jIJUF/6cSmDMMgIX0b/979Af+37xMyTmYAEObXlVvDx/KH8Nvo6NPJto0UEWlmCmexibyS\nXD7Z8xH/3PkPdmT8AkBAqwDuu+x+bgm/ncjA/uq6FpFLlsJZmo1hGPx8fCvv7XyHFXs/prCsAGeT\nM6M7/4Y7e97FiJBozfYkIoLCWZrB6aPk93a+w/aMBABCvEOZ0fNRxvUcT1vPdjZuoYiIfVE4y0Wr\nMCo4XphGal4Kh/JSOZR/iEOnH+elciBnP0XlRdaj5Lsj7uXqDiNxdnK2ddNFROySwlnqLbPoBPuy\n9pGUvZe92XvYl72XpKy9JOf1Bro8AAAgAElEQVQepKSipNptvN186Oofzo1dbtJRsohIPSmcpUZ7\nMnfzr1/fZWvaZpKy93Ki6MR56/i5+9G7zWWEeHekg3cIHbw70ME7lA5eIYR4h+Dj7muDlouItGwK\nZ6miuLyYL/d/xruJb7PhyPcAOJuc6ejTif5BV9DVP5yuft2s3wNaBeiqahGRRlavcJ43bx4JCQmY\nTCZiYmLo06eP9bXly5ezcuVKnJyc6N27N08++SQrVqzg5ZdfJjQ0FIChQ4fywAMPNE0F0igO5hzg\nvZ3v8MGu96xjja/qMJx7IiZybafRuDu727iFIiKXjjrDedOmTSQnJxMXF0dSUhIxMTHExcUBkJ+f\nz7Jly1izZg0uLi5MnDiRn3/+GYAbbriBWbNmNW3r5aIYhsHqg1/xjx1LWZf6NQD+7v480PdBJkTc\nQ5hfNxu3UETk0lRnOMfHxxMdHQ1AWFgYOTk55Ofn4+XlhaurK66urhQWFuLh4cHJkyfx9dU5xpYg\nJTeZx9Y/xP8OrQNgYNvB3B0xkRvDbqaVSysbt05E5NJWZzhnZGQQERFhXTabzaSnp+Pl5YW7uzvT\npk0jOjoad3d3xowZQ+fOndm2bRubNm1i0qRJlJWVMWvWLHr16lXr+/j7e+DiYtuhNRaLt03fv6lZ\nLN6UV5Tz+k+v88TXT1BQWsD1Xa/nxegXuSzoMls3r1FcCp+hI1N9LZ+j19hc9TX4gjDDMKyP8/Pz\nWbJkCatWrcLLy4u7776bXbt20bdvX8xmM8OHD2fbtm3MmjWLzz77rNb9ZmUVNrz1jchi8SY9Pc+m\nbWhKFos3P+zezMPrprE5bRP+7v68eM3fuCX8dkwmk0PUfil8hqqv5XL0+sDxa2zs+moL+jrDOTAw\nkIyMDOvy8ePHsVgsACQlJRESEoLZbAZgwIAB7Nixg1tuuYWwsDAAIiMjyczMpLy8HGdn3XTCFkrL\nS3n+2+d57n/PUVJRwk1hv2feVX/F4mGxddNERKQaTnWtEBUVxerVqwFITEwkMDAQLy8vAIKDg0lK\nSqKoqHJqvx07dtCpUyeWLl3K559/DsCePXswm80KZhtJOL6NUR9fzdPrnsa/lZl3rn+fpde9o2AW\nEbFjdR459+vXj4iICMaOHYvJZCI2NpYVK1bg7e3NqFGjmDRpEhMmTMDZ2ZnIyEgGDBhAhw4d+NOf\n/sSHH35IWVkZc+fObY5aLll5Jbkk5yaTkptMSt7Byu+5yaTkJbMnazcVRgX3Rd7HrH7P4OvuZ+vm\niohIHUzG2SeRbcjW5yla0rmS/NJ8Vh/4khV7P2JL2k9kFmVWu563mw/h/t15YtDT/CHyxhZT34Vq\nSZ/hhVB9LZuj1weOX6NdnXMW+1BSXsL61K9ZsfcjVh34ksKyygvoOvl0pq8lklCfTnT06URHn46E\nenck1Kcjfu7+unuXiEgLpHC2YxVGBRuPxvPJno/4LOlTsoqzAOjs24Xfd7uV33e7lW7+4TZupYiI\nNDaFsx3KLDrB8l/f450dfyc1LwWAQI8g7u8zld93u5XLA/vpiFhExIEpnO1IYsYOlm1fwsd74igq\nL8LDxYOxPe7kD91u48rgYZr/WETkEqFwtrGyijJWHfiSv29/0zoLVEefTkzsPZk7eo7X1dUiIpcg\nhbON5BRn88+d7/CP7Us5lJ8KwNUdRnBfnylEh16ro2QRkUuYwrmZHS88zlsJr/P2jqXkl+bh4eLJ\nPRGTmHTZ/XQ397B180RExA4onKuRVpjGos1/Ib8kH09XTzxdvfB09cTLzcv62NPVixDvULr796jX\nUW5qXgqv/7yY5Tv/SVF5EZbWgTwy4E9M6HWPuq5FRKQKhfM5fjj8Hff/dyLHC9Pqtb6nqxf9AvvT\nP+gK+re9gv5BV9CmdRvr63uz9rB46yI+2ftvyirKCPEOZXrkw4ztcSetXVo3VRkiItKCKZxPqTAq\neHnLQl7Y9BxOJifmDJ3LjWE3UVBaQH5JHgWlBae+8iufK81nb9ZutqT9xHeH/8d3h/9n3Vcnn870\nD7qCk2Un+erA5xgYhPt356F+j/K7rrfg6uxqw0pFRMTeKZyBrKJM7vlgLF/u/ZJ2nu1569p3GNRu\ncL23zynOZkvaZrak/cTmY5vYenwLn+z9NwB9LZE83H8mozuPwclU5zwjIiIiCuetaZv545p7SM1L\nYXjISF6P/nuVbun68HX3Y2RoNCNDo4HKo/Ck7H0UlObT1xKpG4aIiEiDXLLhbBgGb+94i2d+iKGs\noow5V8/h/p4zGmUIk5PJSbfVFBGRC3ZJhnN+SR6PrHuQ/yStIKBVAG+MWsat/W5y6NlURESk5bjk\nwnl7egL3rbmbAzn7Gdh2MEuvfYd2Xu1t3SwRERGrS+YKpcpu7KWM/uQaDuTsZ9rlM/j0pi8UzCIi\nYncuiSPn3OIcHln/IJ8l/R/mVmZevWYJ0R2vs3WzREREquXw4bwtbQt//O+9pOQeZHC7obw5ahnt\nvYJt3SwREZEaOWy3tmEYLEl4jd98ei2puck82v9PrLjpcwWziIjYPYc8cs4qymTGummsOvAFbVpb\neD16KcNDRtq6WSIiIvXikOH81PezWXXgC64KvprXo5cS5NnW1k0SERGpN4cM57si7mVw+6Hc0eMu\nzYssIiItjkOG8+B2QxjcboitmyEiInJBHPaCMBERkZZK4SwiImJnFM4iIiJ2pl7nnOfNm0dCQgIm\nk4mYmBj69OljfW358uWsXLkSJycnevfuzZNPPklpaSmzZ8/myJEjODs788ILLxASEtJkRYiIiDiS\nOo+cN23aRHJyMnFxccydO5e5c+daX8vPz2fZsmUsX76cDz74gKSkJH7++Wc+//xzfHx8+OCDD5gy\nZQoLFy5s0iJEREQcSZ3hHB8fT3R0NABhYWHk5OSQn58PgKurK66urhQWFlJWVsbJkyfx9fUlPj6e\nUaNGATB06FC2bt3ahCWIiIg4ljrDOSMjA39/f+uy2WwmPT0dAHd3d6ZNm0Z0dDQjRoygb9++dO7c\nmYyMDMxmc+UbODlhMpkoKSlpohJEREQcS4PHORuGYX2cn5/PkiVLWLVqFV5eXtx9993s2rWr1m1q\n4u/vgYuLbW8YYrF42/T9m5qj1weOX6Pqa9kcvT5w/Bqbq746wzkwMJCMjAzr8vHjx7FYLAAkJSUR\nEhJiPUoeMGAAO3bsIDAwkPT0dHr06EFpaSmGYeDm5lbr+2RlFV5MHRfNYvEmPT3Ppm1oSo5eHzh+\njaqvZXP0+sDxa2zs+moL+jq7taOioli9ejUAiYmJBAYG4uXlBUBwcDBJSUkUFRUBsGPHDjp16kRU\nVBSrVq0CYN26dQwaNOiiixAREblU1Hnk3K9fPyIiIhg7diwmk4nY2FhWrFiBt7c3o0aNYtKkSUyY\nMAFnZ2ciIyMZMGAA5eXlbNiwgXHjxuHm5sb8+fOboxYRERGHYDLqc0K4Gdi6K0TdMS2fo9eo+lo2\nR68PHL9Gu+rWFhERkealcBYREbEzCmcRERE7o3AWERGxMwpnERERO6NwFhERsTMKZxERETujcBYR\nEbEzCmcRERE7o3AWERGxMwpnERERO6NwFhERsTMKZxERETujcBYREbEzCmcRERE7o3AWERGxMwpn\nERERO6NwFhERsTMKZxERETujcBYREbEzCmcRERE7o3AWERGxMwpnERERO6NwFhERsTMKZxERETuj\ncBYREbEzLvVZad68eSQkJGAymYiJiaFPnz4ApKWlMXPmTOt6qampPPbYY5SWlvLyyy8TGhoKwNCh\nQ3nggQeaoPkiIiKOp85w3rRpE8nJycTFxZGUlERMTAxxcXEABAUF8d577wFQVlbGXXfdxciRI1m9\nejU33HADs2bNatrWi4iIOKA6u7Xj4+OJjo4GICwsjJycHPLz889b79NPP+W6667D09Oz8VspIiJy\nCakznDMyMvD397cum81m0tPTz1vvo48+4pZbbrEub9q0iUmTJnH33Xezc+fORmquiIiI46vXOeez\nGYZx3nPbtm2jS5cueHl5AdC3b1/MZjPDhw9n27ZtzJo1i88++6zW/fr7e+Di4tzQ5jQqi8Xbpu/f\n1By9PnD8GlVfy+bo9YHj19hc9dUZzoGBgWRkZFiXjx8/jsViqbLO+vXrGTJkiHU5LCyMsLAwACIj\nI8nMzKS8vBxn55rDNyursMGNb0wWizfp6Xk2bUNTcvT6wPFrVH0tm6PXB45fY2PXV1vQ19mtHRUV\nxerVqwFITEwkMDDQeoR82vbt2+nRo4d1eenSpXz++ecA7NmzB7PZXGswi4iIyBl1Hjn369ePiIgI\nxo4di8lkIjY2lhUrVuDt7c2oUaMASE9PJyAgwLrNjTfeyJ/+9Cc+/PBDysrKmDt3btNVICIi4mBM\nRnUnkW3A1l0h6o5p+Ry9RtXXsjl6feD4NdpVt7aIiIg0L4WziIiInVE4i4iI2BmFs4iIiJ1ROIuI\niNgZhbOIiIidUTiLiIjYGYWziIiInVE4i4iI2BmFs4iIiJ1ROIuIiNgZhbOIiIidUTiLiIjYGYWz\niIiInVE4i4iI2BmFs4iIiJ1ROIuIiNgZhbOIiIidUTiLiIjYGYWziIiInVE4i4iI2BmFs4iIiJ1R\nOIuIiNgZhbOIiIidUTiLiIjYGYWziIiInVE4i4iI2BmX+qw0b948EhISMJlMxMTE0KdPHwDS0tKY\nOXOmdb3U1FQee+wxrr/+embPns2RI0dwdnbmhRdeICQkpGkqEBERcTB1hvOmTZtITk4mLi6OpKQk\nYmJiiIuLAyAoKIj33nsPgLKyMu666y5GjhzJ559/jo+PDwsXLuT7779n4cKFvPTSS01biYiIiIOo\ns1s7Pj6e6OhoAMLCwsjJySE/P/+89T799FOuu+46PD09iY+PZ9SoUQAMHTqUrVu3NnKzRUREHFed\nR84ZGRlERERYl81mM+np6Xh5eVVZ76OPPuLtt9+2bmM2mwFwcnLCZDJRUlKCm5tbje/j7++Bi4vz\nBRXRWCwWb5u+f1Nz9PrA8WtUfS2bo9cHjl9jc9VXr3POZzMM47zntm3bRpcuXc4L7Nq2OVdWVmFD\nm9KoLBZv0tPzbNqGpuTo9YHj16j6WjZHrw8cv8bGrq+2oK+zWzswMJCMjAzr8vHjx7FYLFXWWb9+\nPUOGDKmyTXp6OgClpaUYhlHrUbOIiIicUWc4R0VFsXr1agASExMJDAw87wh5+/bt9OjRo8o2q1at\nAmDdunUMGjSoMdssIiLi0Ors1u7Xrx8RERGMHTsWk8lEbGwsK1aswNvb23rRV3p6OgEBAdZtbrjh\nBjZs2MC4ceNwc3Nj/vz5TVeBiIiIgzEZ9Tkh3AxsfZ5C50paPkevUfW1bI5eHzh+jXZ1zllERESa\nl8JZRETEziicRURE7IzCWURExM4onEVEROyMwllERMTOKJxFRETsjMJZRETEziicRURE7IzCWURE\nxM4onEVEROyMwllERMTOKJxFRETsjMJZRETEziicRURE7IzCWURExM4onEVEROyMwllERMTOKJxF\nRETsjMJZRETEziicRURE7IzCWURExM4onEVEROyMwllERMTOKJxFRETsjMJZRETEzrjUZ6V58+aR\nkJCAyWQiJiaGPn36WF87evQojz76KKWlpfTq1Ys///nPbNy4kRkzZtCtWzcAwsPDefrpp5umAhER\nEQdTZzhv2rSJ5ORk4uLiSEpKIiYmhri4OOvr8+fPZ+LEiYwaNYpnn32WI0eOADBw4EAWL17cdC0X\nERG5GIaBqSAfU3Y2ppwcnHIqv5tyss95nIMpNwfuGAvX39wsTasznOPj44mOjgYgLCyMnJwc8vPz\n8fLyoqKigi1btrBo0SIAYmNjAUhNTW3CJouIiJxSXFwZrLk5mLKzMOXm4HRu2J71nDV4c3Mql8vL\n6/9ewe3sJ5wzMjKIiIiwLpvNZtLT0/Hy8iIzMxNPT09eeOEFEhMTGTBgAI899hgA+/btY8qUKeTk\n5DB9+nSioqKargoREWmZKiow5eViys6uDNicnDOPs7Mx5WafCdbTIZt71jonTzbo7YzWranw9aPC\nEojRNZwKX18MH18MX18q/PwwfP0rH/v6Yfj6VnncJqwDZOQ30Q+iqnqdcz6bYRhVHqelpTFhwgSC\ng4OZPHky69evp2fPnkyfPp3Ro0eTmprKhAkTWLNmDW5ubjXu19/fAxcX5wuropFYLN42ff+m5uj1\ngePXqPpaNoeszzDg5EnIzoadqViysiofn/5+9uPqXsvJqdxHfTk7g59f5VdIh8rv/v5Vv9f0nJ8f\nJnd3LiZpmuszrDOcAwMDycjIsC4fP34ci8UCgL+/P+3btyc0NBSAIUOGsHfvXoYPH84NN9wAQGho\nKG3atCEtLY2QkJAa3ycrq/CiCrlYFos36el5Nm1DU3L0+sDxa1R9LZtd11dejimnuvOu1RzFnnrN\nlHPWUWxJSYPersLTC8PPD6NdMBU9IzB8fDB8/SqPXH18Mfz8qPDxxfD1O/PY79SRrKcXmEwXVmdu\nCdCwtp6tsT/D2oK+znCOiorilVdeYezYsSQmJhIYGIiXl1flxi4uhISEcPDgQTp16kRiYiJjxoxh\n5cqVpKenM2nSJNLT0zlx4gRBQUGNVpCIiJzFMKCw0Bqs1oDNzjrTVXxW2Jpyc6qGbF5uw97O1bUy\nTH19MTp2xPCp7BJuFWSh0N3zVLD6nglba9dwZcDi0uBO20tOnT+hfv36ERERwdixYzGZTMTGxrJi\nxQq8vb0ZNWoUMTExzJ49G8MwCA8PZ+TIkRQWFjJz5ky+/vprSktLmTNnTq1d2iIil7zS0lPBmnUq\nTKs5iq1yJfE5QVxW1qC3q/D2qTwqDQmlzO9McJ4+v3omWP3OnH/1q3xM69bVHr22snhTYK+9Ay2M\nyTAa0tnfdGzd3WPXXU6NwNHrA8evUfXZuYqK6ofl5ObglJ2FV1kRhUfSrEesp4fnmLJPPS4saNDb\nGa1aYXj7nLqI6dRRbJWAPf34nO7hUxdA4dz41/i0+M+wDnbVrS0icskoLj7rHGvWmXOtdQ3LycnG\nlJuLqaKi1t17nPXYMJlOXQ3sR1nXbtbHVUL2rHOtpwP39FEsrVo17c9CbErhLCKO49xhOaeDtbph\nOTnnXNyUk42pqKhBb2d4eFQOy2nbDqN7T2uwnhme42c9svXt2I7MCtczFzZ5eYOT7qAs1VM4i4j9\nODUsp+p41+wzFzHVNt41O7symBtwps5wdrYelZa1a3cqTP3PGfda3VGsP4aPDzTkWhqLN+UO3OUr\njUvhLCKNq6zs/NA8fXVwLcNyyM2hTXb2BQ/LqQjucCpMfa1XD1cZluPnf17IXtSwHJEmpHAWkapO\n32/43CuGzz4He+5QnNNHsTk5OOU37Ojw9LAcAsyUhYRWBquvb+Wdms66iOn8sK1c1rAccUT6Vy3i\niEpLq3YJVzss5+znz1mnIfcbBmtYlnfqTFl1FzZVCdazhuX4+FqH5Vgs3mSr21cEUDiL2KdqhuVA\nCe4pR6sN2fPCtrBhd9wzWrWqvLCpjQWjS9eq51r9/DB8qo6BrXL06uXdJMNyRC5lCmeRplJUVOXI\ntNphOTXdXKKGYTk+NbyVdViOjx9lXcPPH+N6Olh9fKw3kjD8/K1dxhqWI2JfFM4iNSkvr35YjnW8\nazXDcs6+EKrBw3I8qfDxqXFYjmeHtuQ6tzrvTk4aliPieBTO4rhO32+4ynjX2oflVBme09D7DTs7\nW49Ky4KDT10x7H/mXGuNN5eo37AcT4s3xTonK3JJUDiLfatmWM6Zq4erDsuhMB+/jBNVj25LSxv0\ndhXePpWBefp+w2cHa3XDcs4KWzw9NSxHRBqFwlma1sUMy8nOxqmgYRObu5yeLcfPH6Nj5ypXCp93\nFFtlajpfDcsREbuhv0RSt5KSc4bcnHsR07nB2kjDcjp3sR691jksx9eXgK4hZOSX6ehVRFo8hfOl\noKICsrNxSjlUJTTPXDGcVXPY5mRjOnmyQW9ntG5NhY8vFZZAjLBu1QTr+Rc0VZyaNeeihuV4eECB\nzsmKSMuncG4piorOOdday80lzp6GLqeyixjDIKCeb2U4OZ2ZLSeoR83Dck6HrbdP5bCc07PluLs3\n6Y9CRMTRKZybS3n5mdsb1msC9XOOXouLG/R2FZ5eleHZvj0VPXvhZgmgqLVXNeNez0ygfvrmErrf\nsIiIbSmc66uew3LOm/P1QofluLicmS0nOPiseVz9qnYDn9c9fGpYjqtrlf1ZLN7kaRiOiEiLcGmF\nc2kpptxcnHKyqg7FycmBspN4Hjle7Ww5Fzwsx8u78qi0umE5VbqHz+kq9vWrPH+qo1cRkUuSQ4az\n25qvaPXeO1UvfsrOxlRYUOt2HucsG25uFzYs59R5WA3LERGRC+GQ6eG2ZjXuq7+qer/hsK7WKebO\nXMR05lyrT8f2ZBlu58+WIyIi0swcMpzz//o3CmL/XHlhU33vN2zxpkznZEVExA44ZDhjMlV2K4uI\niLRAmsZGRETEziicRURE7IzCWURExM4onEVEROxMvS4ImzdvHgkJCZhMJmJiYujTp4/1taNHj/Lo\no49SWlpKr169+POf/1znNiIiIlKzOo+cN23aRHJyMnFxccydO5e5c+dWeX3+/PlMnDiRjz/+GGdn\nZ44cOVLnNiIiIlKzOsM5Pj6e6OhoAMLCwsjJySE/Px+AiooKtmzZwsiRIwGIjY2lffv2tW4jIiIi\ntasznDMyMvD397cum81m0tPTAcjMzMTT05MXXniBcePGsXDhwjq3ERERkdo1+CYkhmFUeZyWlsaE\nCRMIDg5m8uTJrF+/vtZtauLv74GLi3NDm9OoLBZvm75/U3P0+sDxa1R9LZuj1weOX2Nz1VdnOAcG\nBpKRkWFdPn78OBaLBQB/f3/at29PaGgoAEOGDGHv3r21blOTrKzCCyqgsVgs3qQ78O07Hb0+cPwa\nVV/L5uj1gePX2Nj11Rb0dXZrR0VFsXr1agASExMJDAzEy8sLABcXF0JCQjh48KD19c6dO9e6jYiI\niNTOZNSjz3nBggVs3rwZk8lEbGwsO3fuxNvbm1GjRpGcnMzs2bMxDIPw8HDmzJmDk5PTedv06NGj\nOeoRERFp8eoVziIiItJ8dIcwERERO6NwFhERsTMKZxERETujcBYREbEzCmcRERE70+A7hLUktc2M\ntXz5clauXImTkxO9e/fmySefpKysjCeffJKUlBTKy8t5/PHHGTBgAHfddReFhYV4eHgAMGvWLHr3\n7m2rsqwaWt+KFSt4+eWXrTeNGTp0KA888AC7du1izpw5AHTv3p1nn33WFuWcp6H1vfHGG2zYsAGo\nvO97RkYGq1evZuTIkbRt2xZn58o70C1YsICgoCCb1HSu2mpcu3Ytb7zxBm5ubowZM4bx48fXuM3R\no0d5/PHHKS8vx2Kx8Ne//hU3NzdblWV1IfW9+OKLbNmyhbKyMu6//36uvfZaZs+eTWJiIn5+fgBM\nmjSJ4cOH26KkKhpa38aNG5kxYwbdunUDIDw8nKefftphPr+PPvqIlStXWtfZsWMH27Zts9u/oQB7\n9uxh6tSp3HPPPdZ/g6dt2LCBRYsW4ezszLBhw5g2bRrQTL+DhoPauHGjMXnyZMMwDGPfvn3Gbbfd\nZn0tLy/PGDFihFFaWmoYhmHce++9xrZt24yPP/7YiI2NNQzDMPbs2WP84Q9/MAzDMMaPH2/s3r27\neQuow4XU98knnxjz588/b1/jx483EhISDMMwjEcffdRYv359M1RQuwup72wrVqwwli5dahiGYYwY\nMcLIz89vppbXX201lpeXG8OGDTNOnDhhlJeXGxMnTjSOHj1a4zazZ882vvzyS8MwDGPhwoXG8uXL\nm7ma811IffHx8cZ9991nGIZhZGZmGldffbVhGIYxa9Ys45tvvmn2GmpzIfX9+OOPxoMPPnjevhzl\n8zt3+zlz5hiGYZ9/Qw3DMAoKCozx48cbTz31lPHee++d9/ro0aONI0eOGOXl5ca4ceOMvXv3Ntvv\noMN2a9c2M5arqyuurq4UFhZSVlbGyZMn8fX15be//S1PPPEEUDlZR3Z2ts3aX5cLqa86JSUlHD58\n2Po/4hEjRhAfH988RdTiYuorKyvjgw8+OO9/wfamthqzsrLw8fHBbDbj5OTE4MGD2bBhQ43bbNy4\nkWuuuQZoGZ9hTfVdccUVvPzyywD4+Phw8uRJysvLbVZDbS6kvpo4yud3ttdee42pU6c2e7sbws3N\njaVLlxIYGHjea6mpqfj6+tKuXTucnJy4+uqriY+Pb7bfQYcN59pmxnJ3d2fatGlER0czYsQI+vbt\nS+fOnXF1dcXd3R2Ad999l9/85jfW7RcvXsydd97JM888Q1FRUfMWU40LqQ8q5+eeNGkSd999Nzt3\n7rT+kp0WEBBgFzOIXWh9AGvWrOHKK6+kVatW1udiY2MZN24cCxYsqNdELM2hthrNZjMFBQUcPHiQ\n0tJSNm7cSEZGRo3bnDx50tqF1hI+w5rqc3Z2tnZ9fvzxxwwbNsx6OuJf//oXEyZM4JFHHiEzM7P5\nCzrHhdQHsG/fPqZMmcK4ceP44YcfABzm8zvtl19+oV27dlXmVLC3v6FQeQvqs/9OnC09PR2z2Wxd\nPl1/c/0OOvQ557Od/Qc5Pz+fJUuWsGrVKry8vLj77rvZtWuX9Rajy5cvJzExkTfffBOACRMm0L17\nd0JDQ4mNjWX58uVMmjTJJnXUpD719e3bF7PZzPDhw9m2bRuzZs3i73//e437sScN+fw++eSTKufN\nH3roIa666ip8fX2ZNm0aq1ev5vrrr2/2Gupydo0mk4n58+cTExODt7c3HTp0qHOb2p6zBw2pb+3a\ntXz88ce8/fbbANx00034+fnRs2dP3nrrLV599VWeeeaZZm1/XepTX6dOnZg+fTqjR48mNTWVCRMm\nsGbNmhr3Y08a8vl9/F0ETxYAAAOFSURBVPHH/O53v7Mut4S/oReqqX4HHfbIubaZsZKSkggJCcFs\nNuPm5saAAQPYsWMHAB999BHffPMNr7/+Oq6urgCMGjXKehHVyJEj2bNnTzNXc74LqS8sLMx6EU1k\nZCSZmZn4+/tX6b5PS0urtounuV3o51dYWMixY8eq/LG4+eabCQgIwMXFhWHDhtnF5we11wgwcOBA\n3n//fZYsWYK3tzfBwcE1buPh4WE9GmkJnyFUXx/Ad999x5tvvsnSpUvx9q6ctWfIkCH07NkTaBm/\ng1B9fUFBQdxwww2YTCZCQ0Np06YNaWlpDvX5QWU3fWRkpHXZHv+G1uXc+k9/Ls31O+iw4VzbzFjB\nwcEkJSVZf5A7duygU6dOpKam8uGHH/Lqq69au7cNw+Cee+4hNzcXqPxHd/pKS1u6kPqWLl3K559/\nDlReoXg63Lp06cLmzZuByi7hq666ygYVVXUh9QHs2rWLLl26WPeTl5fHpEmTKCkpAeCnn36yi88P\naq8R4L777uPEiRMUFhaybt06hgwZUuM2Q4cOtT7fEj5DqL6+vLw8XnzxRZYsWWK9MhvgwQcfJDU1\nFWgZv4NQfX0rV65k2bJlQGW36YkTJwgKCnKYz4//b+9+XRWG4iiAn6EgV6NhMPYHiEXMBkHQ6B9h\nNvojaZMxFBHEpsGmRSwKimCzWI0mURCjrIhDXxgMhIePFXefnE/f4DB2z/hu48Ippkgk4o54ZV1D\n/6LrOizLwvF4hG3bWK/XSKVSH7sHv3rji3e7aY1GI0wmEwQCASSTSVQqFbTbbcxmM2ia5p5jMBhg\ntVqh3+9DCAFVVdFoNCCE8DGZw2u+8/mMcrmM5/MJ27bdXwD2+z3q9ToejwcSiYT7UZzfvOYDgMVi\ngc1m8zLWHg6HmE6nCIVCiMfjqNVqUBTFr1gv3mVcLpfo9XpQFAWFQgH5fP7XY2KxGC6XC6rVKm63\nGzRNg2EY7uTHT17zjcdjdLvdl28ITNPE4XBAs9mEEALhcBiGYSAajfqYzOE1n2VZKJVKuF6vuN/v\nKBaLSKfTX3P9AOdhudPpvLwym8/nUq6hu90OpmnidDohGAxCVVVkMhnouo5sNovtdotWqwUAyOVy\n7ij+E/fgV5czERHRf/S1Y20iIqL/iuVMREQkGZYzERGRZFjOREREkmE5ExERSYblTEREJBmWMxER\nkWRYzkRERJL5AZzMz+OBOzZgAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "peoHmV2M40uU",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 743
+ },
+ "outputId": "f8b96d02-5269-4440-9d6b-a2e6ee06ee50"
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.0000006, n_epochs=1000)"
+ ],
+ "execution_count": 25,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.07932834\n",
+ "Loss after epoch 50 is 0.07932457\n",
+ "Loss after epoch 100 is 0.079320796\n",
+ "Loss after epoch 150 is 0.079317\n",
+ "Loss after epoch 200 is 0.07931324\n",
+ "Loss after epoch 250 is 0.07930946\n",
+ "Loss after epoch 300 is 0.079305686\n",
+ "Loss after epoch 350 is 0.0793019\n",
+ "Loss after epoch 400 is 0.079298116\n",
+ "Loss after epoch 450 is 0.079294346\n",
+ "Loss after epoch 500 is 0.07929058\n",
+ "Loss after epoch 550 is 0.0792868\n",
+ "Loss after epoch 600 is 0.07928302\n",
+ "Loss after epoch 650 is 0.07927924\n",
+ "Loss after epoch 700 is 0.079275474\n",
+ "Loss after epoch 750 is 0.07927168\n",
+ "Loss after epoch 800 is 0.07926792\n",
+ "Loss after epoch 850 is 0.07926414\n",
+ "Loss after epoch 900 is 0.07926037\n",
+ "Loss after epoch 950 is 0.07925659\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.07396706\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAecAAAFKCAYAAAAnj5dkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3Xd4VGX+/vH3pEJ6JkwCpFBCCE2Q\nIgqIFIMo6Ooq68JXxAI2QNFFBWMB1xXRRda2KiK7+lPEKMIusgpYwEYEBYwQhECAEAhlUkklZc7v\nj8BAIIVgkpkM9+u6uJiT055PJpk75znnPMdkGIaBiIiIOA03RzdAREREqlI4i4iIOBmFs4iIiJNR\nOIuIiDgZhbOIiIiTUTiLiIg4GQ9HN+AkqzXfofsPDvYhJ6fIoW1oTK5eH7h+jaqveXP1+sD1a2zo\n+iwW/xrn6cj5BA8Pd0c3oVG5en3g+jWqvubN1esD16+xKetTOIuIiDgZhbOIiIiTUTiLiIg4GYWz\niIiIk1E4i4iIOBmFs4iIiJNROIuIiDgZpxmExBm9+uo/2LnzN7KzsygpKaFt23ACAgKZM+fvDbL9\nMWOuIzQ0DDe3U38jvfbaW797u99//w2XXjqQY8fyWLRoAY8++vjv3qaIiDSdcwrnlJQUJk+ezO23\n38748eOrzFu/fj3z58/H3d2dK664gilTpgAwZ84ckpKSMJlMxMfH07Nnz4ZvfSO7//6HAPjss0/Z\nsyeVqVMfbPB9zJv3Cj4+Pg26zQ8/XEyfPpcQEtJKwSwi0gzVGc5FRUU888wzDBgwoNr5f/vb31i0\naBFhYWGMHz+ekSNHkp2dTVpaGgkJCaSmphIfH09CQkKDN95RNm/+mQ8/fJ+ioiKmTn2I6dOn8r//\nfQXAE088yo033kyXLl2ZM+dp8vPzqaio4MEHH6FTp5hz2v7o0Veetb0tWzZRWFjA/v1pHDx4gAce\nmM6AAYNYtep/LF2agMlkYuzYWygrK2P79m08/PADzJz5JE8//QSLFr3Hhg0beOGFeXh4eGCxhPLY\nY0/x5Zer+fXXX8jNzWH//jT+7/9u5dprb2i075uIiJybOsPZy8uLhQsXsnDhwrPmpaenExgYSJs2\nbQAYMmQIiYmJZGdnExcXB0B0dDR5eXkUFBTg5+d33g2dvf4JPk39z3mvX53rom9g9sC/nde6qam7\nWbJkGV5eXtXO/+ijJVx66UCuu+4G9u7dw8svz+Oll17/Pc3l6NEjzJv3Cj/+uJ7//vcTevW6mHfe\neZt3311CaWkZzz47i7lz5/P2228yb94r5OXl2tedNWsW8+a9SlhYa+bPf54vvliFyWQiNXU3b775\nLw4cSGfWrHiFs4hccEorSlm+aykebh50CoohOqgTfl41j3vdFOoMZw8PDzw8ql/MarViNpvt02az\nmfT0dHJycujevXuVr1ut1lrDOTjYp9ZxS31aeuHmZqqrufXi09KrysDjNQ1C7u/fAh+fU8sGBfnQ\nrVtXwsNDADCZTPZ53t6eBAX5sHNnMtnZ2axduwaA48eLz9q+u7sbjz32EO7ulXUHBwfzyiuvVLs9\nX19vBgy4FIvFn9jYDhw/Xkxe3lFiYjoREWEBYNGihfbttmrlh7t7GR4ebnh6VmAymejRo/LIfejQ\nwfz0009069aNSy7pS+vWQfj7e1JcXFjrQOzNQXNvf11UX/Pm6vVB86vRWmhl3Ec38d3+76p8vY1f\nGzqHdCY2JJbYVrF0DunMkIAhTVZfk1wQZhhGncvU9aSPR3s/xaO9n2qoJtmdfBqWxeJf45Ox8vNL\nKCoqtc/PzS3CMEz2acMw7K8LC4vt8++/fzo9epw6137m9isqbDz33D+qnHO2WvOr3V5h4XE8PVti\nteaTk1NIaWk5eXkllJSUVrvdzMwC8vIKKS+3kZVVWGWbWVnHKCkpJz+/hNJSG1ZrPkVFRVRU2Bz+\ndLDfo7b30BWovubN1euD5lfj9qxkJnw2lv35aVzb8XoGhV9Oau5udufuIjV3N9+mfcs3ad/Yl7+u\n83UsilvcYPuvLeh/VziHhoaSmZlpnz5y5AihoaF4enpW+frRo0exWCy/Z1dOzWQyUVJSAkBKyk4A\nunXrwbffrqNHj57s3buHDRvWM3bs+No2U+v2qtOuXXv270+jqKgId3d3Zsx4iH/845+YTG5UVFTY\nlwsICMBkMnH48GFat27NL79spmfPi6ssIyJyIVm19zPu+3IShWUFPHLJY0zvNwM3U9W7i4vLi9mb\nt4fU3N3szUvl6q5xTda+3xXOERERFBQUcODAAVq3bs3atWuZN28eOTk5vPrqq4wdO5bk5GRCQ0N/\n1/lmZ3fDDWO4++7baN++I7GxXQEYM+bPPPvsbCZPnoTNZuPBBx/+XdurTsuWLZk48V4efHAyAH/+\n8/9hMpno3bsPkydP5PHHZ9uXfeaZZ3j66cdxd3cnPDyCK6+8ijVrPj+/gkVEminDMHh1y0s8++Ns\nWni04O2r3uUPnf5Y7bItPVrSLaQ73UIqT9M2Zc+Ayaijz3nbtm08//zzHDx4EA8PD8LCwhg+fDgR\nERGMGDGCn376iXnz5gFw1VVXMXHiRADmzZvHzz//jMlkYtasWXTp0qXWhji6K6S5dcfUl6vXB65f\no+pr3ly9PnD+GkvKS/jLuvtZmpJAG9+2vDfqQ3paLj7n9Ru6vtq6tesM56bi6DfU2X+ofi9Xrw9c\nv0bV17y5en3g3DUeKTrC7Z+PY9ORn+kb1o93rv6AMN/W9dpGU4azRggTEZFma09eKmv2fc6e3FQM\nTl2AbFRO2ae/3v8lGYUHuSnmZv4x7DVaeLRwXKPPgcJZRESajQpbBZuO/MzqfZ+xet9npOTUfNHs\n6UyYePzSWTzQ5y+YTA17W25jUDiLiIhTKywr5Jv0taze9xlfpK0is7jybqCWHi25usNoRra7ht5h\nfXE3uWPCZA/fyteV2wjwCsLi03zuGlI4i4iI08k7nsuafav4dM9/Wbf/K0oqKm8vDfUJ49ZutzOy\n/TUMjhhKS4+WDm5p41A4i4iIU8gqzmLV3v+xcs9/+fbAOspsZQDEBnfhmg7XcnWHUVwc2ues+5Fd\nkcK5FocOZTBhwlhiYytvAystLeWWW25jyJBh9d7WJ58kkJubyxVXDOXbb9cxceI91S538nGPnp6e\ndW5zz57dzJ//wlmPmRwy5FIuuqiXfTokJITXX3+t3m0+09q1XzJsWBy7du2stQYRkXNhGAapubv5\n5sBaPtvzKeszvqfCqBwc6aJWvbi24x+4Nvp6YoI7O7ilTU/hXIeoqHb28Dt2LI877riFyy4bgLf3\n+V3pFxMTS0xMbI3zTz7u8VzCuSZ+fn4N8lzoM73//rsMGxZXZw0iItWxGTZ+y9rOj4d+IDFjPYkZ\nP2AtPmqf3zesH9d2vIHRHa+jfWAHB7bU8RTO9RAQEEhISCuysrL4978X4uHhybFjufz1r3N54YVn\nycg4SHl5OZMm3Uvfvpfw888beeWVFzGbQwgJaUXbtuFs3vwzy5Z9xN/+9kKtj3t8+eU3WLFiOV9+\nuQqTyY3Bg4cybtx4jh49wpNPzsTT05NOnc79r8kDBw4wefJUFi16D4CJE2/lb397nn/96y1atbKw\nc+dvHDlymKee+huxsV1YvPhd1q37CpPJjXvvncqOHdvZvTuF+PhHGDPmz/YavvrqCxISFuPu7k5s\nbFcefPBhFi1aUO3jLUXkwnOoIIPluz/hx4wf+PHQenKPn3paXmvfNtwYM4bL2gziqvZX09Yv3IEt\ndS7NJpx9Zz+B96cN+8jI49fdQOHsc39k5KFDGRw7lkdoaBhQOWb1jBmPs2rV/wgJacVjjz1Fbm4u\n06bdy7vvfsiCBa/x5JPPEBPTmYcffoC2bU/94BUVFdb6uEer9Sjr1n3F668vAuC++yYybFgcy5Yl\ncOWVV3HzzeN4//132L075Xd/H0pLS5k//zX+85+lrFr1P3x8fFi37isWLHiHjIyDvP/+O8yc+SSL\nF7/LnDl/Z/Pmn0/UUMRbb/2Tf//7A3x8fHj00Yfs8858vKXCWeTCUlZRxlu/vsHff3qOovJCAKIC\n2jOy/SgGtr2cy9oOpH1Ah2ZxW5MjNJtwdpT9+9OYOvVuoPLZ1k888bT9EZrdulWOt7pt268kJW3h\n119/AeD48eOUlZVx6NAhYmIqj24vvrgPx48ft2933769REW1x9u7Bd7eLZg7d36V/f72WzIHDqRz\n//2V53WLigo5fDiDffv2MmxY5eDrvXv348cf15/V5oKCAnubAaKjOzF5cs3nh3v16g2AxRLG9u3J\npKTspFu3Hri5uREREcnMmU9Wu156+n4iIqLsT9Xq3bsvKSk7AOjZs3JIvNDQUAoKCmrct4i4nvUH\nv2fmd9PZkf0b5hZmnhzwNFe3H0W4f4Sjm9ZsNJtwLpz9t3od5TaU0885n8nDw9P+/4QJdzJixNVV\n5ru5nbqi8MxRUt3c3DEMW4379fDwZMCAQTz66ONVvr548buYTlypWNP61Z1zLi09VmW6vLzc/vrk\n86RPttPd3Q2bre5RXU2mqnWVl5fh7e1d7TZFxPUdLjjM/V8+yNKUBEyYmNDtTuIvexJzixBHN63Z\ncf3r0ZtAt249+P77ymd+5uRks2DBPwFo1crC/v37MAyDLVs2VVnn9Mc9Hj9+nAcfnIxhGPbHPcbG\ndmXz5k2UlJRgGAYvvTSP48dLiIpqx44d2wHsXcjnws/Pj5ycbAzDICsrk4yMAzUuGxvbla1bkygv\nLyc7O4vHHqt8otaZgR0Z2Y4DB/ZTVFTZZbVly2ZiY7udc5tExDWU28p5+9c3iX0tlqUpCfSy9Obz\nm75i3tCXFMznqdkcOTuz4cPj2Lz5J+69904qKiq4887KLuW7757ME0/MoHXrNvbz1CfV9bjHV199\ni5tvHseUKXfh5ubGFVcMxdu7BX/60ziefHIm3367lujomHNuY2BgIP369WfSpAl06hRT69XWbdq0\nZeTIUUydejeGYXDPPVMA6Nw5lrvumsB99z1gr2HKlGlMn34/JpMbPXteTK9eF/Pzzxvq9f0TkeZr\nw6Efif/uEbZmJhHUIojnr5jPhG534O7mXvfKUiM9leoEZ36aSkNw9frA9WtUfc2bK9VnGAbfHfyG\nlze9yHcHK3sNx3a5hZevnY+pyDVH7AI9lUpERJyQYRisSVvFS5v+zqYjlafVhkYO5+F+j9G/zaVY\nfP2xFrnGHyCOpnAWEZFaVdgqWJG6nJc2vchv2ckAXNPhWh7sM53eYX0d3DrXpHAWEZFqZRQc5Iu0\n1bz+yyvszduDm8mNm2JuZlrf6XQxd3V081yawllERIDKMF6f8T3rD37PDxnfsTdvDwBebl7c2u0O\npvaeRofAjg5u5YVB4SwicgEpqygj53gOOSXZ5JRksz8/jR8z1lcJYwB/rwCuanc1A8MHc0OnGzW0\nZhNTOIuIuBjDMNiamcSnqf9la2YSOSXZZJdkk1OSw7HSvGrXOT2MB7W9nB6teup2KAdSOIuIuADD\nMPjV+gsrUv/DitTlpB3bZ5/n7e6NuUUIEf6RmFv0IriFmWBvMyEtzVhahnJJ60sVxk5G4Swi0kwZ\nhkGSdcuJQP4P+08Eso+HL3/sdBPXRf+RIZFD8fP01wMmmhmFs4hIM7TVmsSUr+5mR/ZvAPh6+nFj\nzBiui/4jw6PiaOnhuoOBXAgUziIizYhhGPxr20Jm/RBPqa2UGzrdyA2dxjAs6koFsgtROIuINBN5\nx3N5aO39rNzzX0JahPDalQu4st1Vjm6WNAKFs4hIM7D5yM/cveYO9uencVmbgSwY8S/a+LV1dLOk\nkeiRkSIiTswwDN5Meo3rlo8kPX8/f+n3KMuuX6lgdnHndOQ8Z84ckpKSMJlMxMfH07NnT/u8L7/8\nkjfeeAMvLy9Gjx7N+PHj2bBhA9OmTSMmpvKRhp07d+bJJ59snApERFxUdkkW076ezOp9n2NpGcrr\ncQsZEjnM0c2SJlBnOG/cuJG0tDQSEhJITU0lPj6ehIQEAGw2G8888wzLly8nKCiIu+66i7i4OAD6\n9+/PK6+80ritFxFxESXlJezN28Pu3F2k5u5id+4uvj2wjsOFhxgcMZTX4xYS5hNW94bEJdQZzomJ\nifbAjY6OJi8vj4KCAvz8/MjJySEgIACz2QzAZZddxvr16wkP1zBvIiLVKasoY2fODn61/sL2rG3s\nzt3F7tzdHMjfj82wVVnW292bmf2fYFqf6Rog5AJTZzhnZmbSvXt3+7TZbMZqteLn54fZbKawsJB9\n+/YRHh7Ohg0b6N+/P+Hh4ezevZt7772XvLw8pk6dyqBBg2rdT3CwDx4ejv3hq+3B167A1esD169R\n9TUvx8uPs/XoVjYf2szmDZvZdGgTW49s5XjF8SrLhfmGcXnU5cSGxBIbEkvnkM7EtoqlQ1AHPN09\nHdT68+Nq7+GZmqq+el+tbRiG/bXJZGLu3LnEx8fj7+9PREQEAO3bt2fq1Klcc801pKenM2HCBNas\nWYOXl1eN283JKTqP5jcci8Ufq9V1HxLu6vWB69eo+pyfYRgkZ23ji32rWJO2iiTrFspt5fb5Xm5e\ndA3pTk/LxfS09KJHq4voFBRDoHfQ2RuzQW52CVDSdAX8Tq7wHtamoeurLejrDOfQ0FAyMzPt00eP\nHsVisdin+/fvzwcffADAiy++SHh4OGFhYYwaNQqAqKgoWrVqxZEjR4iMjDzvIkREnFFxeTE/HPyW\n1ftW8cW+VWQUHgTA3eTOxaG9K4O41cUMjR2EhUi83Gs+SBE5qc5wHjRoEK+++ipjx44lOTmZ0NBQ\n/Pz87PMnTZrE888/T8uWLVm7di133HEHK1aswGq1MnHiRKxWK1lZWYSF6UIGEXENRWVF/Gf3J3y+\ndyXfHlhHcXkxAEHeQdwUczNXtb+aYZFXEtQi2L6Oqx9VSsOqM5z79OlD9+7dGTt2LCaTiVmzZrFs\n2TL8/f0ZMWIEN998M3feeScmk4m7774bs9nM8OHDefjhh/nqq68oKytj9uzZtXZpi4g0B1nFWfxr\n21v8a+tbZJVkAdA5OJYR7a5mZPtr6Ne6Px5uGttJfj+TcfpJZAdy9F+Urv5XravXB65fo+pznH15\ne3kz6TWW7Hif4vJigryDuKPHJMZ2GU+HwI7ntA1nrq+huHqNTnXOWUTkQvXL0c38c8srfLrnP9gM\nG5H+Udzbawrjut6Kn6df3RsQOU8KZxGREwzDYGfODtZnfM+nu//DDxnfAdCjVU+m9p7GH6L/qG5r\naRL6KRMRl1JQms+irW+RV5pHpH8U7QLaEenfjgj/yLMeqWgzbOzM3sH6jO/44eD3/HjoBzKLT92d\nMiRiGFN7P8gVEUMxmUxNXYpcwBTOIuISDMNgRepynvohnkOFGdUuE+oTRpR/O6ICoigpP86Ph34g\nuyTbPr+tbzhjOv+ZgW0vZ1D44HM+nyzS0BTOItLs7cpJYeZ3D/PdgXV4u3szvd8MhkQOJ/1YGun5\n+9l/4v+0/DS2HN3Ez0c2AhDuF8GfOl/FoPDBDGx7Oe0C2usIWZyCwllEmq2CsgL+8fPfeTPpNcps\nZVwZNYJnB79Ax8BoAC5rM+Csdcpt5RwuPISBQYRfpMJYnJLCWUSaHcMwWLnnvzz5/WNkFB4k0j+K\nv13+PFe3H1Vn2Hq4eRDhr9EKxbkpnEWk2Si3lfNN+te8kfRPvj2wFi83Lx7q+zDT+jyMj6ePo5sn\n0mAUziLi1AzDYFvWVj7auYRlKR9jLT4KwLDIK3lu8N/pGNTJwS0UaXgKZxFxSocLD/FJysd8tHMJ\nv2UnAxDsHcwdPSbxp85j6Rt2ic4Xi8tSOIuI0zAMgy/SVrFo61t8c2AtNsOGp5snozpcx82x44hr\nd5We6iQXBIWziDicYRis2LmCp76aTZJ1CwB9wy7h5thxXN/pj5hbhDi4hSJNS+EsIg5jGAar9n3G\nvJ/msjUzCRMmro++kYf6PUK3kO6Obp6IwyicRaTJGYbB53v/x7yf57It81dMmBjbYyyTezxEF3NX\nRzdPxOEUziLSZArLClm193+8tuVlkrO2YsLEjTFjeKjvo1wee4lLP25QpD4UziLSqErKS/hq/xf8\nZ9cnrEn7nOLyYtxMbtwY8yf+0vdROptjHd1EEaejcBaRBldaUcq3B9ayfNcnfL73fxSUVR4RRwd1\n4oZON/Gnzn/W/ckitVA4i8jvYjNspOfvZ1fOTlJyUtietY01+z4n93guAJH+UdzRYxI3dLqRHq16\n6t5kkXOgcBaRc1ZUVsTX+79kR/Z2exin5u6ipKKkynKtfdtwT+z/cUPMTfQJ7adAFqknhbOI1OnY\n8TzeSV7Em0mvkVmcaf96S4+WxATHEhPcmc7BscQEx9I5OJZOQTG4u7k7sMUizZvCWURqlFWcxcJf\nX+ftrW9xrDSPAK9A7u/9EAPaDqRzcBci/CNxM7k5upkiLkfhLCJnOVSQwetJr/Je8r8pKi+iVctW\nPH7pLO7oMYkA70BHN0/E5SmcRcRuX95eXt3yEgk7FlNqK6WNb1viL32K8d1u1yMZRZqQwllE2JWT\nwsubX+STlI+oMCpoH9CBB/r8hT/FjsXb3dvRzRO54CicRS5gyZnbeGnTPFakLsfAoIu5K9P6TOf6\nTjfi4aaPBxFH0W+fyAXol6Obmb/p76za+z8ALmrVi4f6PsKojtfqAi8RJ6BwFrlAHK84TmLGD7yZ\n9Bpf7/8SqHws4/R+j3Jl1FW6F1nEiZxTOM+ZM4ekpCRMJhPx8fH07NnTPu/LL7/kjTfewMvLi9Gj\nRzN+/Pg61xGRxldhq+BX6y98d/Abvj3wDRsPJdoHCxnUdjAP9XuEweFDFMoiTqjOcN64cSNpaWkk\nJCSQmppKfHw8CQkJANhsNp555hmWL19OUFAQd911F3Fxcezfv7/GdUTk/GWXZFFWUYbNsFFhVGAz\nbCf+VWAzDIrKC9l46Ee+PfgN6w9+z7HSPPu6Xc3dGRxxBddF/5FL21zmwCpEpC51hnNiYiJxcXEA\nREdHk5eXR0FBAX5+fuTk5BAQEIDZbAbgsssuY/369aSnp9e4jojU3968Pdyy6hG+2PPFOa/TPqAD\n13f6I4PDhzAwfDChPqGN2EIRaUh1hnNmZibdu3e3T5vNZqxWK35+fpjNZgoLC9m3bx/h4eFs2LCB\n/v3717pOTYKDffDwcOxwfxaLv0P339hcvT5wvRrLKsqYnzif2d/MpqS8hIGRA4kMiMTdzR03kxvu\npsr/T772dPekT5s+XNnhStoFtXN08+vN1d6/M7l6feD6NTZVffW+IMwwDPtrk8nE3LlziY+Px9/f\nn4iIiDrXqUlOTlF9m9KgLBZ/l37Qu6vXB65X46YjPzF93TS2Z22jVUsL71z/DsNCrzm3c8RlNLvv\nhau9f2dy9frA9Wts6PpqC/o6wzk0NJTMzFMD3R89ehSLxWKf7t+/Px988AEAL774IuHh4Rw/frzW\ndUSkZgWl+czZ8FcWbX0LA4PxXW/jyQFP0zmynUt/8InIKXXe0Dho0CBWr14NQHJyMqGhoVW6pydN\nmkRWVhZFRUWsXbuWAQMG1LmOiFRv1d7PuHxJf97euoDooE7894bPmT/sVYJbmB3dNBFpQnUeOffp\n04fu3bszduxYTCYTs2bNYtmyZfj7+zNixAhuvvlm7rzzTkwmE3fffTdmsxmz2XzWOiJSvfT8/azZ\n9zkrU1fwQ8Z3eLl58XC/mUzrO11DZ4pcoEzGuZwQbgKO7q7TuZLmr7nUaBgGSdYtrNr3Gav3fk5y\n1lb7vMHhQ3hu8Dw6m2PPWq+51He+VF/z5+o1OtU5ZxE5fzbDhrXYyuGCDNLz0/nmwFpW7/uMw4WH\nAPBy8+LKqBGMbD+Kke2voY1fWwe3WEScgcJZpAFkFBxkRepyDuSnc6jwEIcKMjhceIjDRYcot5VX\nWdbcwsyfY/+Pke1HMTRqOH6euh5DRKpSOIv8DrtyUnhty0ssTUmgzFZm/7qHmwdhPq3pZelNG9+2\ntPFtQ2u/tlwS1p9LWl+Ku5tj7+kXEeemcBY5D5uP/Mwrm//B53tXYmDQKSiGe3pN4WJLb1r7tcXS\n0qKnO4nIeVM4i5wjwzBYl/41r275B98f/BaA3qF9eKDPdK7pMFphLCINRuEsUouyijKSs7ay8dCP\nJOxcwtbMJACGRg7ngT5/YVDbwXqqk4g0OIWzyGnyjufy8+GNbDz8IxsPbWDL0U0UlVcOLetmcuP6\n6Bu5v8+D9LRc7OCWiogrUziLyyurKGNd+ldkFmdSVF5EcXkxxaf/X1ZMUXkhO7J/Y2f2Dgwqb/03\nYaKLuSuXtL6M/m0uZVDbwYT7Vz9+vIhIQ1I4i8sqrSglYecHvLzpRfbnp9W5vI+HD4PCB9O/9aX0\nb3MZfcMuIdA7qAlaKiJSlcJZXE5pRSlLdrzPK5vnk56/H293b+7scRcXh/bBx8OHlh4taenpQwv3\nFrT08KGlZ0taurekVUsLnu6ejm6+iIjCWVzH8fLj/Hvb27yyeT4HCw7Qwr0F9/SczJTe02jt28bR\nzRMROWcKZ2n2jlcc5/3t7/LaL//gYP5BWnq05N5eU5nSexphPmGObp6ISL0pnKXZqrBV8Mmuj3h+\n47Ok5+/Hx9OHyRc/wOSLHyDUJ9TRzRMROW8KZ2l2DMPg6/1f8MyPs9metQ1vd2/u63U/s0c8gamo\npaObJyLyuymcpVnZdOQnnkmcxfqM7zFhYmyXW3j0kngi/COx+PpjLXLdx9WJyIVD4SzNwu6cXczZ\n8FdW7vkvACPajeTxy2bTLaS7g1smItLwFM7itGyGjR8OfseSHe+zfNdSKowK+oZdwlMD/sqAtoMc\n3TwRkUajcBansysnhY92LmFpSgIHCw4A0CkohvhLZzG643Uay1pEXJ7CWZxCdkkWy3d9wkc7P2DL\n0c0A+HsFML7rbdwcO47+bS7TU59E5IKhcBaHsRk21qV/zf9L/jdfpK2izFaGm8mNK6NGcHPsOK7u\nMJqWHrr6WkQuPApnaXLWIitLdrzP/9v+b/Yf2wdAt5Ae/Dn2/7gxZgxhvq0d20AREQdTOEuTMAyD\nxIwfeDd5ESv3rKDMVkZLj5bEUZtOAAAgAElEQVTc0nUCt3W/k4tD+zi6iSIiTkPhLI2irKKMQ4UZ\npOfv51drEu9vf4dduSkAxAZ34fYeExnT+c966pOISDUUznJeDMPgaPFRdueksDdvD+n5aaTnp3Mg\nP530/P0cKszAZtjsy3u5eXFTzM3c1mMil7a+TFdci4jUQuEstSq3lbMvby8pOTvZnZvCrpyUE//v\n4lhp3lnLu5ncaOPblktaX0qEXyRRAVG0C+jAVe2voVXLVg6oQESk+VE4S7X25e3l3eR/sWTHe2SX\nZFeZ5+nmScfAaAZHDCEmqDMdg6KJ9I8i0j+KNr5t9UxkEZHf6ZzCec6cOSQlJWEymYiPj6dnz572\neYsXL2bFihW4ubnRo0cPHn/8cZYtW8bLL79MVFQUAAMHDuS+++5rnAqkwVTYKvhy/xr+vW0ha/d/\nhYFBSIsQxna5hc7BXYgJ7kxMUAxRAe3xcNPfdSIijaXOT9iNGzeSlpZGQkICqampxMfHk5CQAEBB\nQQGLFi1izZo1eHh4cOedd/LLL78AMGrUKGbMmNG4rZcGcbToKB/89v/4f8n/5kBBOgCXtL6UO3pM\n4rroG/B293ZwC0VELix1hnNiYiJxcXEAREdHk5eXR0FBAX5+fnh6euLp6UlRURE+Pj4UFxcTGBjY\n6I2WhnEw/wDP/DiLT1P/Q5mtDB8PXyZ0u5Pbe0ykR6uLHN08EZELVp3hnJmZSffup578YzabsVqt\n+Pn54e3tzZQpU4iLi8Pb25vRo0fToUMHtmzZwsaNG5k4cSLl5eXMmDGDbt26NWohcu4Mw+C97e8w\ne/0TFJTln7i1aRI3x47F3yvA0c0TEbng1fvEoWEY9tcFBQUsWLCAVatW4efnx2233caOHTvo1asX\nZrOZoUOHsmXLFmbMmMGnn35a63aDg33w8HCvfwUNyGLxd+j+G5vF4s/enL1M+nQSX+/9mkDvQBb9\nYRF3XHyHy9zadCG8h65M9TV/rl5jU9VXZziHhoaSmZlpnz569CgWiwWA1NRUIiMjMZvNAPTr149t\n27YxZswYoqOjAejduzfZ2dlUVFTg7l5z+ObkFP2uQn4vi8UfqzXfoW1oTCGtfHlh7XyeSZxNUXkh\nI9qNZN6Ql2nj15bMzAJHN69BuPp7qPqaN1evD1y/xoaur7agr/MxP4MGDWL16tUAJCcnExoaip+f\nHwDh4eGkpqZSUlICwLZt22jfvj0LFy5k5cqVAKSkpGA2m2sNZmlce/JSGfbuMB777hG83D3555Vv\n8f6oj2jj19bRTRMRkWrUeeTcp08funfvztixYzGZTMyaNYtly5bh7+/PiBEjmDhxIhMmTMDd3Z3e\nvXvTr18/IiIieOSRR/jwww8pLy/n2WefbYpa5DSGYZBdks1HO5cwd+MzFJcXM6rDdTw/ZD5hPmGO\nbp6IiNTCZJx+EtmBHN0V0hy7Y8oqyth3bC9px/aSdmwfacfSTvy/j/3H0igoq6wnpEUIr1/7OkMt\nV7vMueXqNMf3sD5UX/Pm6vWB69fYlN3aGkmimTEMg58Ob+STXQn8d/eys0bvAvDx8KVdQHvaBbSj\nc3AX7r14Kl2jOrj0L42IiCtRODcTu3JS+CQlgU92fUzaiWcgt2ppYWyXW+gYGE1UQLsTgdyBkBYh\nLn2ELCLi6hTOTuxI0RH+s2spn6R8xC/WLUDlUfGYzn9mTOc/c0XEUA2jKSLigvTJ7oQ2H/mZt359\ngxWpyym3leNucicu6ipu6nwzV3cYja+nr6ObKCIijUjh7CTKKsr4354VLPj1dTYd+QmA2OAuTOh+\nBzd0GoPFx+LgFoqISFNRODtYdkkW729/l0Vb3+JQYQYAV7W7mrt63scVEUN17lhE5AKkcHaQPbm7\n+ecvr7I05UOKy4vx9fRj0kX3MOmie+gY1MnRzRMREQdSODex37K28/Lmefxn9zJsho2ogPbcddE9\njOsyngBvPdFLREQUztVKzd3F04lPUVhagK+nL76efvh6+uHn5Yevpy9+nv74evoS4R9J37B+BHoH\n1bnNpKNb+MemeXy2t/IBIN1DLuKhvg8zuuMfcHfT0KYiInKKwvkMn6b+l2lfT7aPrlUXEyZizV3o\nF9affq370y+sP52CY3AzVQ5bvuHQj/xj0wt8vf9LAPqG9eOhvo8wop1rj9YlIiLnT+F8QllFGbN+\neJw3kl7Fx8OHN0cs4rqON1BYVkBhWSGFZYUUlOVXeb0rZyc/Hd7I5iOb2JH9G+//9i4AQd5B9A27\nhKLyIhIzfgBgUNvBPNTvEQaHD1Eoi4hIrRTOwJHCw9y0ciLf7f+O6KBO/PvqxXQxdwUgyD2YoBbB\nta5fbivnt+zt/Hx4Iz8d3sDPhzfy1f4vABgeFceDfR/hsjYDGr0OERFxDRd8OCdm/MBda27naNER\nrou+gZeGvYa/V0C9tuHh5sFFrXpyUaue3NFjEgDWIiuFZQW0D+zQGM0WEREXdsGGs2EYvJH0Gs8k\nPgXA/Kvmc0v0xAbrcrb4WLCggUNERKT+Lshwzi89xrSvp7Byz38J9Qnj7ave5bpeI/XUJhERcQoX\nXDhvy9zKpNUT2JOXyoC2g3jrqncI8wlzdLNERETs3BzdgKZiGAbvbX+HUZ9cyZ68VKZcPI1P/vCp\ngllERJzOBXHkXFBWwKPfPMTSlASCvIN4e+S7XNX+Gkc3S0REpFouH847s3cwcfWtpOTspE9oXxaO\nfJdI/yhHN0tERKRGLt2t/dHOJYxcOpSUnJ3c03MyK/64WsEsIiJOzyWPnIvLi3n8u0d5/7d38fcK\nYNHI97gu+npHN0tEROScuGQ4nwzmi1r14u2R79IhsKOjmyQiInLOXDKcr+kwmnD/CKZcPI0WHi0c\n3RwREZF6cclwHtH+aka0v9rRzRARETkvLn1BmIiISHOkcBYREXEyCmcREREnc07nnOfMmUNSUhIm\nk4n4+Hh69uxpn7d48WJWrFiBm5sbPXr04PHHH6esrIyZM2eSkZGBu7s7zz33HJGRkY1WhIiIiCup\n88h548aNpKWlkZCQwLPPPsuzzz5rn1dQUMCiRYtYvHgxS5YsITU1lV9++YWVK1cSEBDAkiVLuPfe\ne3nxxRcbtQgRERFXUmc4JyYmEhcXB0B0dDR5eXkUFBQA4OnpiaenJ0VFRZSXl1NcXExgYCCJiYmM\nGDECgIEDB7J58+ZGLEFERMS11BnOmZmZBAcH26fNZjNWqxUAb29vpkyZQlxcHMOGDaNXr1506NCB\nzMxMzGZz5Q7c3DCZTJSWljZSCSIiIq6l3vc5G4Zhf11QUMCCBQtYtWoVfn5+3HbbbezYsaPWdWoS\nHOyDh4d7fZvToCwWf4fuv7G5en3g+jWqvubN1esD16+xqeqrM5xDQ0PJzMy0Tx89ehSLxQJAamoq\nkZGR9qPkfv36sW3bNkJDQ7FarXTp0oWysjIMw8DLy6vW/eTkFP2eOn43i8UfqzXfoW1oTK5eH7h+\njaqveXP1+sD1a2zo+moL+jq7tQcNGsTq1asBSE5OJjQ0FD8/PwDCw8NJTU2lpKQEgG3bttG+fXsG\nDRrEqlWrAFi7di2XXnrp7y5CRETkQlHnkXOfPn3o3r07Y8eOxWQyMWvWLJYtW4a/vz8jRoxg4sSJ\nTJgwAXd3d3r37k2/fv2oqKhg/fr1jBs3Di8vL+bOndsUtYiIiLgEk3EuJ4SbgKO7QtQd0/y5eo2q\nr3lz9frA9Wt0qm5tERERaVoKZxERESejcBYREXEyCmcREREno3AWERFxMgpnERERJ6NwFhERcTIK\nZxERESejcBYREXEyCmcREREno3AWERFxMgpnERERJ6NwFhERcTIKZxERESejcBYREXEyCmcREREn\no3AWERFxMgpnERERJ6NwFhERcTIKZxERESejcBYREXEyCmcREREno3AWERFxMgpnERERJ6NwFhER\ncTIKZxERESejcBYREXEyHuey0Jw5c0hKSsJkMhEfH0/Pnj0BOHLkCA8//LB9ufT0dKZPn05ZWRkv\nv/wyUVFRAAwcOJD77ruvEZovIiLieuoM540bN5KWlkZCQgKpqanEx8eTkJAAQFhYGO+99x4A5eXl\n3HrrrQwfPpzVq1czatQoZsyY0bitFxERcUF1dmsnJiYSFxcHQHR0NHl5eRQUFJy13PLlyxk5ciS+\nvr4N30oREZELSJ3hnJmZSXBwsH3abDZjtVrPWu7jjz9mzJgx9umNGzcyceJEbrvtNrZv395AzRUR\nEXF953TO+XSGYZz1tS1bttCxY0f8/PwA6NWrF2azmaFDh7JlyxZmzJjBp59+Wut2g4N98PBwr29z\nGpTF4u/Q/Tc2V68PXL9G1de8uXp94Po1NlV9dYZzaGgomZmZ9umjR49isViqLLNu3ToGDBhgn46O\njiY6OhqA3r17k52dTUVFBe7uNYdvTk5RvRvfkCwWf6zWfIe2oTG5en3g+jWqvubN1esD16+xoeur\nLejr7NYeNGgQq1evBiA5OZnQ0FD7EfJJW7dupUuXLvbphQsXsnLlSgBSUlIwm821BrOIiIicUueR\nc58+fejevTtjx47FZDIxa9Ysli1bhr+/PyNGjADAarUSEhJiX+e6667jkUce4cMPP6S8vJxnn322\n8SoQERFxMSajupPIDuDorhB1xzR/rl6j6mveXL0+cP0anapbW0RERJqWwllERMTJKJxFREScjMJZ\nRETEySicRUREnIzCWURExMkonEVERJyMwllERMTJKJxFREScjMJZRETEySicRUREnIzCWURExMko\nnEVERJyMwllERMTJKJxFREScjMJZRETEySicRUREnIzCWURExMkonEVERJyMwllERMTJKJxFRESc\njMJZRETEySicRUREnIzCWURExMkonEVERJyMwllERMTJKJxFREScjMe5LDRnzhySkpIwmUzEx8fT\ns2dPAI4cOcLDDz9sXy49PZ3p06dz9dVXM3PmTDIyMnB3d+e5554jMjKycSoQERFxMXWG88aNG0lL\nSyMhIYHU1FTi4+NJSEgAICwsjPfeew+A8vJybr31VoYPH87KlSsJCAjgxRdf5Pvvv+fFF1/kpZde\natxKREREXESd3dqJiYnExcUBEB0dTV5eHgUFBWctt3z5ckaOHImvry+JiYmMGDECgIEDB7J58+YG\nbraIiIjrqjOcMzMzCQ4Otk+bzWasVutZy3388ceMGTPGvo7ZbK7cgZsbJpOJ0tLShmqziIiISzun\nc86nMwzjrK9t2bKFjh074ufnd87rnCk42AcPD/f6NqdBWSz+Dt1/Y3P1+sD1a1R9zZur1weuX2NT\n1VdnOIeGhpKZmWmfPnr0KBaLpcoy69atY8CAAVXWsVqtdOnShbKyMgzDwMvLq9b95OQU1bftDcpi\n8cdqzXdoGxqTq9cHrl+j6mveXL0+cP0aG7q+2oK+zm7tQYMGsXr1agCSk5MJDQ096wh569atdOnS\npco6q1atAmDt2rVceuml59VwERGRC1GdR859+vShe/fujB07FpPJxKxZs1i2bBn+/v72i76sVish\nISH2dUaNGsX69esZN24cXl5ezJ07t/EqEBERcTEm41xOCDcBR3eFqDum+XP1GlVf8+bq9YHr1+hU\n3doiIiLStBTOIiIiTkbhLCIi4mQUziIiIk5G4SwiIuJkFM4iIiJORuEsIiLiZBTOIiIiTkbhLCIi\n4mQUziIiIk5G4SwiIuJkFM4iIiJORuEsIiLiZBTOIiIiTkbhLCIi4mQUziIiIk5G4SwiIuJkFM4i\nIiJORuEsIiLiZBTOIiIiTkbhLCIi4mQUziIiIk5G4SwiIuJkFM4iIiI1sdkw5ebglrYPysqabLce\nTbYnERERRygtxZSbi1teLqa8E//n5mLKyzv1+lgebrmV86t8Pf8YJsOo3M6NN8Kb7zRJkxXOIiLi\n3AwDiorsgel2LK8yOHNzTr3Oy60M19ND9uSyRUX12p3N1w8jMBBbeAS2oCCMwECMwCBa3H5rIxV4\nNoWziIg0Pput8ijUfgSbV/V1Xi5uuTlVQrbK/Hp0KRsmkz1Qy2NiMQIrA7YyaIOwnZhnBAVhCwjE\nOBHAtsBgjMBA8PSsdrstLP5gzW+o70itzimc58yZQ1JSEiaTifj4eHr27Gmfd+jQIf7yl79QVlZG\nt27d+Otf/8qGDRuYNm0aMTExAHTu3Jknn3yycSoQEZGmUVZ2KjBzc04dpZ44QqW0CL9DR3E7EbaV\ny554fSzvVPfwOTA8PSuDNCgYo12HKkewtqAgjIAT4XoieO2vg4Iw/PzBrXlfUlVnOG/cuJG0tDQS\nEhJITU0lPj6ehIQE+/y5c+dy5513MmLECJ5++mkyMjIA6N+/P6+88krjtVxEROrHMKC4+FT3sP3c\n65lHsGccuZ4M2aLCOnfR8vTd+fhiCwrC1rYttq7dKoMz4NQRbOXRahBGUPBZIUvLlmAyNd73wsnV\nGc6JiYnExcUBEB0dTV5eHgUFBfj5+WGz2di0aRPz588HYNasWQCkp6c3YpNFRC5gp3cP28+95lY9\n95p32jnY0wM3L7f+3cMBJ7qHO8Wc3T18ImxPBmpQh3CybR51dg9L3eoM58zMTLp3726fNpvNWK1W\n/Pz8yM7OxtfXl+eee47k5GT69evH9OnTAdi9ezf33nsveXl5TJ06lUGDBjVeFSIizUlZ2YkrgnPO\numr4rCPYk1cPn3xd3+5hD49TXb7t2lUJVVtQ8NnnXk9/7R9Qv+5hiz8VTXRO1tXV+4Iw47QfCsMw\nOHLkCBMmTCA8PJy7776bdevW0bVrV6ZOnco111xDeno6EyZMYM2aNXh5edW43eBgHzw83M+vigZi\nsfg7dP+NzdXrA9evUfU5CcOAkhLIyan6Lze35uncXCwnXxfW3T1cha8vBAVBZAQEX1T5Ojj41P8n\n/50+feK1yccHk8nUZINaNJv38Dw1VX11hnNoaCiZmZn26aNHj2KxWAAIDg6mbdu2REVFATBgwAB2\n7drF0KFDGTVqFABRUVG0atWKI0eOEBkZWeN+cnLqd6l7Q7NY/LG68F98rl4fuH6Nqq+B2WyYCvJr\nuXo45+xu4dNv0yktPeddGSYTpsBAKgICsXXsdPa519OOVqt+rbIbmVoObGpVZIOigvNb9zzoZ7T+\n26tJneE8aNAgXn31VcaOHUtycjKhoaH4+flVruzhQWRkJPv27aN9+/YkJyczevRoVqxYgdVqZeLE\niVitVrKysggLC2uwgkREgFPdw8dyazj3elqwnnE+1nTsGCab7Zx3Ze8eDgjEiIw8LVyDq1wpXO1t\nOgGBWMICyXbh4JKGVWc49+nTh+7duzN27FhMJhOzZs1i2bJl+Pv7M2LECOLj45k5cyaGYdC5c2eG\nDx9OUVERDz/8MF999RVlZWXMnj271i5tEbmAnbh6GGs6HnsOVp6HPeOcq1veGQNNnDwPW1i/o0LD\nxwdbYBC21m0wYrvWct9r8GlXEp+4etjH54K+elialskw6nFlQSNydFeIumOaP1ev0WnrM4zKq4fz\nzrj1xn4Em1M1XM+8Xef48Xrtznba1cFV73sNrOG+12D7OufdPdwAnPb9a0CuXqNTdWuLyAWgvPzU\n1cPVjtx09hXE9u7hvLz6dw+fPCo9rXu4RetQirx87OFa5dzrycEl/APA3bEXjoo0BYWziKsoKTlj\nQP+cqgP6n3FBU5Xu4YL6HQ0YLVtWdg+HhmHExNZ432uVcD0RyPj6Vts93MLiT6ELH3WJ1IfCWcRZ\nGEbl1cNndg+fCFDKivDLOFLzKE717R72D8AICqKifQfKa+oeDgqqOorTye5hb+9G+iaICCicRRpW\nRUXVp+GcNURiDaM4HcurDN2Kilo3X2VoRHd3e4iWh4efuLCphltzTr4+7ephPPTrL+Ks9NspcqaT\n3cP2I9gzrx6u4b7XvDzc8o/Va1dGixaV3cOWUIzomGrGHA6yj+IU2K4N2YbXqauHa+geFpHmT+Es\nrscwMBUWnP0w9bwzuoprevZrSUm9dmfz868MzMgoyk8/91rdfa+BQacd4QZCixbnviMNjShywVA4\ni3OqqDh1PvXMh6mf9bXKR9eRf4yQ7Oxz6h4+neHubj9SLQ8Przrm8GlHsFWOZtU9LCKNSJ8q0niO\nHz/tgqbcM64krubI9fTB/+vbPeztDcHB2FpZKruHqxytBmIEBld/sVNQEIavn7qHRcSpKJylZie7\nh6u97zWn+ltzTr8IqgG6h+1Hq2fd9xpc9dmvLVpgsfiTo25fEXEBCmdXd6J7mHwrHnsOnHXfa5VR\nnM4M17w8TOXl57wrw83NPmJTeZs2Z189fObITad3Gat7WETETp+GzUFp6WkXMeVUfcD6maM4nRmu\n+cfsz34NPoddGV5elaFqDsHoEF316uGTg/yfMebwycA1/PzVPSwi0gAUzk3BMKCwsIb7XqsZuelE\n2NqPbIvq9zhNm69fZXBGRNrPvXq3tlDk7XP2QBMBp8692gKDoGXLuncgIiKNSuF8rmy26q8ernI+\ntoZzr3l5mMrKznlXhsl0qns4JvaMI9faRnGqPKqtrnvYoqERRUSajQsrnEtLT7siOKfKuVfKi/E9\neKTGq4dP7x4+F4an54kgDcZo16H+3cNubo34jRAREWfmkuHsteZzWrz3ztkhW0f3sM8Z0/bu4fCI\nasL1zPteT+seDgis7B7W+VcRETkPLhrOq/Fe/XnV7uFOnc8asen07uGAdm3JwetU0AYGgqeno0sR\nEZELkEuGc8Hf/0HhrL9WDi5xrt3DFn/KdU5WREScgEuGMyZT5UPZRUREmiFddSQiIuJkFM4iIiJO\nRuEsIiLiZBTOIiIiTkbhLCIi4mQUziIiIk5G4SwiIuJkFM4iIiJORuEsIiLiZBTOIiIiTkbhLCIi\n4mRMhlGPhxSLiIhIo9ORs4iIiJNROIuIiDgZhbOIiIiTUTiLiIg4GYWziIiIk1E4i4iIOBkPRzeg\nMc2ZM4ekpCRMJhPx8fH07NnTPm/x4sWsWLECNzc3evToweOPP055eTmPP/44+/fvp6KigkcffZR+\n/fpx6623UlRUhI+PDwAzZsygR48ejirLrr71LVu2jJdffpmoqCgABg4cyH333ceOHTuYPXs2ALGx\nsTz99NOOKOcs9a3vjTfeYP369QDYbDYyMzNZvXo1w4cPp3Xr1ri7uwMwb948wsLCHFLTmWqr8csv\nv+SNN97Ay8uL0aNHM378+BrXOXToEI8++igVFRVYLBb+/ve/4+Xl5aiy7M6nvhdeeIFNmzZRXl7O\nPffcw1VXXcXMmTNJTk4mKCgIgIkTJzJ06FBHlFRFfevbsGED06ZNIyYmBoDOnTvz5JNPusz79/HH\nH7NixQr7Mtu2bWPLli1O+xkKkJKSwuTJk7n99tvtP4MnrV+/nvnz5+Pu7s4VV1zBlClTgCb6HTRc\n1IYNG4y7777bMAzD2L17t3HzzTfb5+Xn5xvDhg0zysrKDMMwjDvuuMPYsmWLsXTpUmPWrFmGYRhG\nSkqKcdNNNxmGYRjjx483du7c2bQF1OF86vvkk0+MuXPnnrWt8ePHG0lJSYZhGMZf/vIXY926dU1Q\nQe3Op77TLVu2zFi4cKFhGIYxbNgwo6CgoIlafu5qq7GiosK44oorjKysLKOiosK48847jUOHDtW4\nzsyZM43PPvvMMAzDePHFF43Fixc3cTVnO5/6EhMTjUmTJhmGYRjZ2dnGkCFDDMMwjBkzZhhff/11\nk9dQm/Op78cffzTuv//+s7blKu/fmevPnj3bMAzn/Aw1DMMoLCw0xo8fbzzxxBPGe++9d9b8a665\nxsjIyDAqKiqMcePGGbt27Wqy30GX7dZOTEwkLi4OgOjoaPLy8igoKADA09MTT09PioqKKC8vp7i4\nmMDAQP7whz/w2GOPAWA2m8nNzXVY++tyPvVVp7S0lIMHD9r/Ih42bBiJiYlNU0Qtfk995eXlLFmy\n5Ky/gp1NbTXm5OQQEBCA2WzGzc2Nyy67jPXr19e4zoYNG7jyyiuB5vEe1lTfJZdcwssvvwxAQEAA\nxcXFVFRUOKyG2pxPfTVxlffvdP/85z+ZPHlyk7e7Pry8vFi4cCGhoaFnzUtPTycwMJA2bdrg5ubG\nkCFDSExMbLLfQZcN58zMTIKDg+3TZrMZq9UKgLe3N1OmTCEuLo5hw4bRq1cvOnTogKenJ97e3gC8\n++67XHvttfb1X3nlFW655RaeeuopSkpKmraYapxPfQAbN25k4sSJ3HbbbWzfvt3+S3ZSSEiIfTuO\ndL71AaxZs4bLL7+cFi1a2L82a9Ysxo0bx7x58zCcZFC82mo0m80UFhayb98+ysrK2LBhA5mZmTWu\nU1xcbO9Caw7vYU31ubu727s+ly5dyhVXXGE/HfH+++8zYcIEHnroIbKzs5u+oDOcT30Au3fv5t57\n72XcuHH88MMPAC7z/p3066+/0qZNGywWi/1rzvYZCuDh4VHlc+J0VqsVs9lsnz5Zf1P9Drr0OefT\nnf6BXFBQwIIFC1i1ahV+fn7cdttt7Nixgy5dugCV5zOTk5N58803AZgwYQKxsbFERUUxa9YsFi9e\nzMSJEx1SR03Opb5evXphNpsZOnQoW7ZsYcaMGbz99ts1bseZ1Of9++STT6qcN3/ggQcYPHgwgYGB\nTJkyhdWrV3P11Vc3eQ11Ob1Gk8nE3LlziY+Px9/fn4iIiDrXqe1rzqA+9X355ZcsXbqUf/3rXwBc\nf/31BAUF0bVrV9566y1ee+01nnrqqSZtf13Opb727dszdepUrrnmGtLT05kwYQJr1qypcTvOpD7v\n39KlS/njH/9on24On6Hnq7F+B132yDk0NLTKX3JHjx61/xWXmppKZGQkZrMZLy8v+vXrx7Zt2wD4\n+OOP+frrr3n99dfx9PQEYMSIEfaLqIYPH05KSkoTV3O286kvOjrafhFN7969yc7OJjg4uEr3/ZEj\nR6rt4mlq5/v+FRUVcQ+wg1kAAAM1SURBVPjw4SofFjfccAMhISF4eHhwxRVXOMX7B7XXCNC/f38+\n+OADFixYgL+/P+Hh4TWu4+PjYz8aaQ7vIVRfH8B3333Hm2++ycKFC/H39wdgwIABdO3aFWgev4NQ\nfX1hYWGMGjUKk8lEVFQUrVq14siRIy71/kFlN33v3r3t0874GVqXM+s/+b401e+gy4bzoEGDWL16\nNQDJycmEhobi5+cHQHh4OKmpqfZv5LZt22jfvj3p6el8+OGHvPbaa/bubcMwuP322zl27BhQ+UN3\n8kpLRzqf+hYuXMjKlSuByisUT4Zbx44d+fnnn4HKLuHBgwc7oKKqzqc+gB07dtCxY0f7dvLz85k4\ncSKlpaUA/PTTT07x/kHtNQJMmjSJrKwsioqKWLt2LQMGDKhxnYEDB9q/3hzeQ6i+vvz8fF544QUW\nLFhgvzIb4P777yc9PR1oHr+DUH19K1asYNGiRUBlt2lWVhZhYWEu8/5BZTD5+vrau3id9TO0LhER\nERQUFHDgwAHKy8tZu3Ytgwb9//bu11VhKI4C+LkoyBVMhsHwDxCLmF8QhBn9I8xGfyQ1yRgOEcSm\nwaZFLAqK2aJRTCZBEKNYRNEXhMHg8WDFzXE+fYPDuDvjuzv287E16Ou/Upmmic1mAyEE6vU6drsd\nIpEINE3DcDjEeDxGIBBAKpVCuVxGq9XCdDqFqqrWOfr9PpbLJXq9HqSUUBQFjUYDUkoXk705zXc6\nnVAqlfB6vfB4PKxPAPb7PWq1Gp7PJ5LJpLUpzm1O8wHAfD7HarWyjbUHgwEmkwlCoRASiQSq1SqE\nEG7Fsvkv42KxQLfbhRAC+XweuVzuz2Pi8TjO5zMqlQputxtUVYWu69bkx01O841GI3Q6HdseAsMw\ncDgc0Gw2IaVEOByGruuIRqMuJntzmu96vaJYLOJyueB+v6NQKCCdTvvm+gHvh+V2u217ZTabzTx5\nD91utzAMA8fjEcFgEIqiIJPJIBaLQdM0rNdrmKYJAMhms9Yo/hNr0NflTERE9I18O9YmIiL6Vixn\nIiIij2E5ExEReQzLmYiIyGNYzkRERB7DciYiIvIYljMREZHHsJyJiIg85hd//zeyhygSMgAAAABJ\nRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "KjY_KnlE5ClG",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "## Drive the loss to a minimum."
+ ]
+ },
+ {
+ "metadata": {
+ "id": "JKiHjGN15HPX",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 743
+ },
+ "outputId": "c5091e69-1974-49b7-a037-c6b404178acd"
+ },
+ "cell_type": "code",
+ "source": [
+ "# YOUR CODE HERE\n",
+ "linear_regression(learning_rate=0.05, n_epochs=1000, interval=50)"
+ ],
+ "execution_count": 28,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.07932834\n",
+ "Loss after epoch 50 is 0.028722776\n",
+ "Loss after epoch 100 is 0.015420757\n",
+ "Loss after epoch 150 is 0.008280054\n",
+ "Loss after epoch 200 is 0.0044467766\n",
+ "Loss after epoch 250 is 0.0023889972\n",
+ "Loss after epoch 300 is 0.0012843404\n",
+ "Loss after epoch 350 is 0.00069133844\n",
+ "Loss after epoch 400 is 0.00037300243\n",
+ "Loss after epoch 450 is 0.00020211392\n",
+ "Loss after epoch 500 is 0.0001103778\n",
+ "Loss after epoch 550 is 6.113317e-05\n",
+ "Loss after epoch 600 is 3.4696594e-05\n",
+ "Loss after epoch 650 is 2.0505682e-05\n",
+ "Loss after epoch 700 is 1.2886845e-05\n",
+ "Loss after epoch 750 is 8.797734e-06\n",
+ "Loss after epoch 800 is 6.6026278e-06\n",
+ "Loss after epoch 850 is 5.424036e-06\n",
+ "Loss after epoch 900 is 4.791539e-06\n",
+ "Loss after epoch 950 is 4.451873e-06\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 5.2130513e-06\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAe0AAAFKCAYAAAAwrQetAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvNQv5yAAAIABJREFUeJzs3XdgTff/x/HnHdn3RnLjxghKU4Ko\nVU0Ru6FV3xqtolbV3tSWml97pURRFNWiTau0VI1SWkptURQVe1RuhsjNzbrj94dfb79axEjc3Jv3\n4x/33HPPue+3k+R1z7jno7DZbDaEEEIIke8pHV2AEEIIIR6OhLYQQgjhJCS0hRBCCCchoS2EEEI4\nCQltIYQQwklIaAshhBBOQu3oAh7EYEh1dAn4+3uTnGxydBl5Rvpzbq7eH7h+j9Kf88vtHvV67X3n\nyZ52DtRqlaNLyFPSn3Nz9f7A9XuU/pzf0+xRQlsIIYRwEhLaQgghhJOQ0BZCCCGchIS2EEII4SQk\ntIUQQggnIaEthBBCOAkJbSGEEMJJ5Oubq+RH8+d/wJkzv5OUlEhGRgbFiwfh61uIqVNn5cr6W7d+\nncDAIiiVf3+e+vDDJU+83j17fuKll2pz+3YKy5YtZsSI9594nUIIIZ6uhwrts2fP0rdvX7p06ULH\njh3vmrd3716ioqJQqVTUq1ePfv36ATB16lRiY2NRKBRERkZSuXJlbty4wYgRI7BYLOj1embNmoW7\nu3vud5WHBgx4D4Dvv9/I+fNx9O8/ONffY/bsaLy9vXN1nV98sZrq1V8kIKCwBLYQQjipHEPbZDIx\nadIkatWqdc/5kydPZtmyZRQpUoSOHTvyyiuvkJSUxKVLl4iJiSEuLo7IyEhiYmKIjo6mffv2NG3a\nlKioKNauXUv79u1zvSlHOHLkEF98sQqTyUT//u8xdGh/Nm3aAcCYMSN44402lC9fgalTJ5KamorF\nYmHw4OE891zZh1p/s2Yv/2t9R48eJi3NyOXLl7h27SoDBw6lVq1wtmzZxNq1MSgUCtq160B2djan\nTp1g2LCBjBo1lokTx7Bs2WccOXKIFSsWY7Mp0OsDGT16HNu3b+X48WPcupXM5cuXaN++E//5T8s8\n+38TQgjx8HIMbXd3d5YuXcrSpUv/Ne/KlSsUKlSIYsWKAVC/fn327dtHUlISERERAAQHB5OSkoLR\naGT//v1MnDgRgIYNG7J8+fInCu0Je8ewMe6bx17+Xl4PbsmE2pMfa9m4uHN8/vm6+x49+PLLz3np\npdq8/npLLlw4z7x5s5k7d+GTlEt8/E1mz47m11/38u23X1OlSlU++eRjVq78nKysbKZMGc/06VF8\n/PFHzJ4dTUrKLfuys2dP49NPV6JWa4iKmsEPP2xBoVAQF3eOjz5aztWrVxg/PlJCWwhRIF1LvcrO\nKzuoE1SP0oXKOLoc4CFCW61Wo1bf+2UGgwGdTmef1ul0XLlyheTkZEJDQ+963mAwkJ6ebg+0gIAA\nDAbDA9/b39/7gfd09fZyR6lU5NTCI/H2cv/XzdrvdfN2rdYTb++/X+vn503FihUICgoAQKFQ2Od5\neLjh5+fNmTMnSUpKYufObQBkZqb/a90qlZLRo99DpbrTt7+/P9HR0fdcn4+PB7VqvYReryUkpAyZ\nmemkpMRTtuxzlCihB2DZsqX29RYurEGlykatVuLmZkGtVtk/cDVoUJeDBw9SsWJFXnzxBYoW9UOr\ndSM9Pe2BN693Bs5ef05cvT9w/R6lv/zHarPS7Jt3OHj9IACh+lCahzSneUhzwoLCUCqUcOsWfP01\nvPUWer3vU6nrqVyIZrPZHuq5f8pp1JQR1cYxotq4x67rfv53dDG9XnvP0cZSUzMwmbLs827dMmGz\nKezTNpvN/jgtLd0+f8CAoVSqVPme7wVgsViZNu2Du85pGwyp91xfWlombm5eGAypJCenkZVlJiUl\ng4yMrHuuNyHBSEpKGmazlcTENMxmi339iYm3ycgwk5qaQVaWFYMhFZPJhMVizRejrT2u+20/V+Hq\n/YHr9yj95U+fnfqEg9cPEl68Lhp3DT9d2cm0PdOYtmcaeq9ARiWE0nvFMbwTksHfH0Pdxrn23nk2\nyldgYCAJCQn26Zs3bxIYGPiv5+Pj49Hr9Xh7e5ORkXHXa12VQqEgIyODjIwMzp49A0DFipX4+edd\nAFy4cJ4vvlj1ROu7l2eeKc3ly5cwmUxkZmYyeHBfbDYbCoUSi8Vif52vry8KhYLr168DcOzYEcqX\nr/AYnQohhGtJzkhiyq8T8HHTsKjxx3z2Wgynu17k06Zf0DuoDYs+T2HIrJ2okpMZH+HG/heKPrXa\nnii0S5QogdFo5OrVq5jNZnbu3El4eDjh4eFs3boVgJMnTxIYGIhGo6F27dr257dt20bdunWfvIN8\nqmXL1vTs+Q5Tp04kJOROGLZu3ZZr167Qt293ZsyYTNWq1Z9offfi5eVFt269GTy4LwMG9OL111ui\nUCioVq06fft2u+uc9ogRYxg6dCj9+/fEbDbz8stNHr9hIYRwEVP3TyIpI4nhL46mqM+dU4jeai9a\nxKazYNQO3jyWSfLz5Zkz9x12tq2NxqvQU6tNYcvhOPWJEyeYMWMG165dQ61WU6RIERo1akSJEiVo\n3LgxBw8eZPbs2QA0adKEbt26ATB79mwOHTqEQqFg/PjxlC9fnvj4eEaOHElmZibFixdn2rRpuLm5\n3fe988MhFWc9tPOwpD/n5ur9gev3KP3lL7HxR2mytgHl/EP4sc0vuKncUN78E83IoXh8vxGbpydp\no8eR3rMP/P+1R7nd44MOj+cY2o6UHza0s/3APSrpz7m5en/g+j1Kf/mH1Wal2brGHL55kK+bb6Ru\nUD08YtagGTsaZcotsmqFY/xgPpZnn7truacZ2nJHNCGEEAKIOb2GwzcP0iL4DerzLNq338T9x+1Y\nfTSkTp9DRpduoHTs3b8ltIUQQhR4tzKSmfTrOHyU3sy/VBn/PjVRGlPJqt+Q1Kj5WEuWcnSJgIS2\nEEIIwYyDU9BeS2D/T2UoGTsBq28hbs9bSGa7DqDI3fuBPAkJbSGEEAXabzePolm6lBM/KvDOukDm\nK00xzpqLtWgxR5f2LxLaQgghCizl2TMEdG7G3PM2MgtpuR09l8xWrfPV3vX/ktB+RDduXKdz53aE\nhJQHICsriw4d3qF+/YaPvK6vv47h1q1b1KvXgJ9/3kW3br3u+bq/htV80Nfj/nL+/Dmiomb+azjP\n+vVf4vnnq9inAwICmDhx2iPX/E87d26nYcMI/vjjzAN7EEKIfMVsxmvhfDxnTiIgy8zPYcWpuGI3\nNr3e0ZU9kIT2YyhV6hl7KN6+ncK773agZs1aeHh4Ptb6ypYNoWzZkPvO/2tYzYcJ7fvRaDS5Mi73\nP61atZKGDSNy7EEIIfIL1amTaAf1xS32KPEaJQNbuzNy0g/YtPk7sEFC+4n5+hYiIKAwiYmJrFix\nFLXajdu3b/Hf/05n5swpXL9+DbPZTPfuvXnhhRc5dOgA0dFz0OkCCAgoTPHiQRw5coh1675k8uSZ\nDxxWc968RWzYsJ7t27egUCipW7cBb7/dkfj4m4wdOwo3Nzeee67cQ9d+48Z1evUazeLFKwHo1q0T\nkyfPYPnyJRQurOfMmd+5efNPxo2bTEhIeVavXsmuXTtQKJT07t2f06dPce7cWSIjh9O6dVt7Dzt2\n/EBMzGpUKhUhIRUYPHgYy5YtvucwokIIkRdSs27zycnlGEzx2LBhs1lRZpl5df0Rmn19FLXZyuZa\ngXSoG0/vBiMpoS3p6JIfilOHts+EMXhszN2hOTNfb0nahIcfmvPGjevcvp1CYGAR4M49vUeOfJ8t\nWzYREFCY0aPHcevWLQYN6s3KlV+wePGHjB07ibJlyzFs2ECKFw+yr8tkSnvgsJoGQzy7du1g4cJl\nAPTp042GDSNYty6Gl19uQps2b7Nq1SecO3f2if8fsrKyiIr6kG++WcuWLZvw9vZm164dLF78Cdev\nX2PVqk8YNWosq1evZOrUWRw5cuj/ezCxZMkCVqxYg7e3NyNGvGef989hRCW0hRC5zWazsSFuPWP2\njOKm6U/789Wvw4pvoHI8XPGFnq/DlrLxPOdXlj5VBziw4kfj1KHtKJcvX6J//57AnfHGx4yZaB++\ntGLFO0OSnjhxnNjYoxw/fgyAzMxMsrOzuXHjBmXL3tkbrlq1OpmZmfb1Xrx4gVKlSuPh4YmHhyfT\np0fd9b6//36Sq1evMGDAnfPGJlMaf/55nYsXL9Cw4Z3xy6tVq8Gvv+79V81Go9FeM0Bw8HO0a9fx\nvj1WqVINAL2+CKdOneTs2TNUrFgJpVJJiRIlGTVq7D2Xu3LlMiVKlLKPUlat2gucPXsagMqVqwJ3\nBpoxGo33fW8hhHgcF1LOM+rnoey8sgMPlQcjXoykSdH6BC/6lFIrvkBpsXC9TUsuDx9ApFbD+ygI\n0pbAU/14pzYdwalDO23C5EfaK84t/3tO+5/Uajf7v507d6Vx41fvmq/8n7vp/PMOskqlCpvNet/3\nVavdqFUrnBEj3r/r+dWrV6JQKP9/nfde/l7ntP/888Zd02az2f74r/G8/6pTpVJiteZ8x1uF4u6+\nzOZsPDw87rlOIYTIDZmWTD48Ope5h2eTacmkQclGTK83h3JnEtC27Yv63B9YSpXm1gfzcatbn4c/\niZj/OPZ+bC6sYsVK7NnzEwDJyUksXrwAgMKF9Vy+fBGbzcbRo4fvWianYTVDQipw5MhhMjIysNls\nzJ07m8zMDEqVeobTp08B2A9FPwxvbx8SExOx2WwkJiZw/frV+742JKQCv/0Wi9lsJikpkdGjhwH8\nK8hLlnyGq1cvYzKlAXD06BFCQio+dE1CCPEodl/9iQYxtZhxYAp+Hv4sabyCmIareH7WEvxeb4Iq\n7hymnn1I+mkf2XXrO7rcJ+bUe9r5WaNGERw5cpDevbtisVjo2vXOoemePfsyZsxIihYtZj8P/pf/\nHVYToG3b9ncNqzl//hLatHmbfv16oFQqqVevAR4enrz11tuMHTuKn3/eSXBw2Yeu0dfXl9q1a9O9\ne2eee67sA6/+LlasOK+88hr9+/fEZrPRq1c/AMqVC6FHj8706TPQ3kO/foMYOnQACoWSypWrUqVK\nVQ4d2v9I/39CCPEgBpOBcb+M5us/vkSpUNL9+V6MChtDwIFjaNvXRnXpIubnypL6wQLML9V0dLm5\nRkb5yoEzjVDzOKQ/5+bq/YHr9yj9PRqbzca6P77i/T0jSMpIoqq+GrPqz6WqVzA+E8fh9elybEol\n6f0HkzZsFHjm/flqGeVLCCGE+IcbxuuM+Pk9tl7cjLfam0nh0+j+fG+8du5AM7Q9quvXMFcIJXXe\nAsxVqzu63DwhoS2EECJfs9lsfH56FeN+ieR2Vgp1guoR1WA+ZayF0Azsi+eXn2NTq0kbPhrToKHg\n7u7okvOMhLYQQoh860rqZYbsHMBPV3eicdMyq/5cOlXsguf3m9CMHIIq/ibZVaqROncBltBKji43\nz0loCyGEyHesNiufnFzGpH3jScs28nKpxsyuP48SGR5oenbF89t12Dw8MI6ZSHrfAaAuGHFWMLoU\nQgjhFGw2Gz9c2sLsg9M5ZjhKIQ8/5jf6iDbl2uH5zddoIoejTEoiu0YYqfMWYinrzN+6fnQS2kII\nIRzOarOy5cL3zDk0g98SYgFo+dwbTAqfTrFUG5ou7fHY8j02Ly+Mk6eT3q0X/M8NmwoKCW0hhBAO\nY7VZ2XR+A3MOzeRU4gkUKGj13JsMfmE4FXQV8PhiNZqxo1HeTiGrTj1S50RjLfOso8t2GAltIYQQ\nT53FamFj3DdEHZ7J6aTfUSqUvFm2De+9MJxyuhCUVy6j7dMK910/YtVoSZ01l4xOXUBZsG/kKaEt\nhBDiqbqdmcKbG5oTaziKSqGibUh7Br8wlGC/smC14rl8KT6TxqNMM5LVKILU2fOwlnCOoTPzmoS2\nEEKIp8ZitdDrh67EGo7yn2dbMKbWBJ4tFAyA8nwc2iEDcN+7B2shP25HLyKzbfs7IxEJQEJbCCHE\nUzRl/0R2XP6BBiUbsaTJCtRKNVgseC1ZhM/0SSjS08ls+h+MM6OwFinq6HLzHQltIYQQT8XaszF8\neHQuzxYKZknjO4GtOnMa7eC+uB0+hLVwYVKjF5HZvJXsXd+HhLYQQog8dyz+CEN2DkDjpuXTpl/g\np9LgPXc23rOno8jKIuON1hgnz8RWuLCjS83XHiq0p06dSmxsLAqFgsjISCpXrmyft337dhYtWoS7\nuzvNmjWjY8eOfPXVV2zYsMH+mhMnTnD06FE6deqEyWTC29sbgJEjR1Kpkuvfdk4IIQqym6abvLO5\nPZmWTJa98ikVrmWiHdwIt99isRQpinHmB2Q1beboMp1CjqF94MABLl26RExMDHFxcURGRhITEwOA\n1Wpl0qRJrF+/Hj8/P3r06EFERARvvfUWb731ln35zZs329c3bdo0ypUrWHewEUKIgirTnMm7mztw\nI+0646uPpcUXh/COjkJhNpPevhNpEyZj8/N3dJlOI8cvvO3bt4+IiAgAgoODSUlJwWg0ApCcnIyv\nry86nQ6lUknNmjXZu3fvXcsvWLCAvn375kHpQggh8jObzUbfTX05dPMAIxWNGDP8K3yiZmItWoxb\nMesxzl0ggf2IctzTTkhIIDQ01D6t0+kwGAxoNBp0Oh1paWlcvHiRoKAg9u/fT1hYmP21x48fp1ix\nYuj1evtz0dHRJCcnExwcTGRkJJ5PYYByIYQQT9/Hv33EmoPL+eTXQDrv3IXCaiX93e6kjZ2ITaN1\ndHlO6ZEvRLPZbPbHCoWC6dOnExkZiVarpUSJEne9du3atbRq1co+3blzZ0JCQihVqhTjx49n9erV\ndOvW7b7v5e/vjVrt+HvL6vWu/cMl/Tk3V+8PXL9HV+xvx/kdbFszmhMbVAQnxENwMCxbhlf9+ng5\nurg88LS2YY6hHRgYSEJCgn06Pj7+rj3nsLAw1qxZA8CcOXMICgqyz9u/fz9jxoyxTzdu3Nj+uFGj\nRnz//fcPfO/kZNNDtJC39HotBkOqo8vIM9Kfc3P1/sD1e3TF/v64coS4/q+xa58Vm0KBqXd/0kaN\nAW9vcLFeIfe34YM+AOR4Tjs8PJytW7cCcPLkSQIDA9FoNPb53bt3JzExEZPJxM6dO6lVqxYAN2/e\nxMfHB3d3d+DOHnqXLl24ffs2cCfQy5Yt+/hdCSGEyHeubVhOUEQjeu7LIqlUERS//ELaf6feCWzx\nxHLc065evTqhoaG0a9cOhULB+PHjWbduHVqtlsaNG9OmTRu6du2KQqGgZ8+e6HQ6AAwGg/0x3DmU\n3qZNG7p06YKXlxdFihRhwIABedeZEEKIp0ZxO4WMkb2p+vUmzArY3z6CZ6evgZJ6l9y7dhSF7X9P\nUucz+eGQkSseuvpf0p9zc/X+wPV7dIX+3Ldtxn1IP7ziE4gtAr9PHs3LLUYDrtFfTp7m4XG5I5oQ\nQojHokhKRDNmFJ5rY8hSwfiGCkqOX0yLiu0cXZrLKtgDkwohhHgs7hu/RVcnDM+1MRwKUvBSbzVl\npq2SwM5jsqcthBDioSni49GOHobHxm8we7gR+YqK+bVULH1tFY1Lv+ro8lyehLYQQoic2Wx4rI1B\nM2YkyuRkblYJoVH9OC4EurOy6ec0KNnI0RUWCBLaQgghHkh5/Rqa4YPx+GErVm9vNvZ9jTf0W3B3\n8+LzZl9RO6iOo0ssMCS0hRBC3JvNhueqlfhMGIMy9Tbnqz1H6yZJHPX6Hn8Pfz577UvCir3k6CoL\nFAltIYQQ/6K8dBHtkIG4795FhrcHo1v7Mjf0HBp3LUOrjKR3lX4U8vBzdJkFjoS2EEKIv1mteC5f\ngs+kCSjTTfxQwYN3X83kVmE33qs8jN5V+uPvqct5PSJPSGgLIYTAmG3kxrGdPDt6PNrj50j2VjCg\nFayvrqRb5ffoW3UgAV4Bji6zwJPQFkKIAmb/jV+JjT/CuVt/EHfrHBcSz9Juxw3+uxO8zPBVRRje\n3INmNXtysOog9N76nFcqngoJbSGEKCAS0xMZ9fNQvo1bZ38u9CZs/M6dqlcgpZAXmwe9ia35m2wN\nrIrOU/as8xsJbSGEKAA2nd/I8J8Gk5Bu4MWiL9GrYg8afvUrZT5eiSI7i4zWbcmePJ26Ognq/ExC\nWwghXFhSRiKRu4ez7o+1eKg8mFB7Cv0Ix6/PANQnf8NStBjG2XPJatLU0aWKhyChLYQQLmrLhe8Z\numsghvR4XihSg/nh86iybB1eH76MwmIhvUNn0iZMxlZIvrrlLCS0hRDCxdzKSOb9PSP56uwXuCvd\nGVvrvwzMDsPvzXdR/3EWS6lnSJ0TTXb9ho4uVTwiCW0hhHAhJxNO0O67N7hp+pOq+mosqD2Pqh/F\n4LWkKQqbDVP3XqRFjgeNxtGliscgoS2EEC4i05JJ3+3duWn6k1FhYxiWHoZfq3dQXbyA+dlgjHMX\nkF2ztqPLFE9AQlsIIVzEB4dm8nvSKXqW6cS4L2/g9UlzbEolpn6DSBsRCV5eji5RPCEJbSGEcAHH\nDceYdySKDtcKs2Dpj6ivXcNcvgKp8xZirvaCo8sTuURCWwghnFyWJYv3N/ZkyXoLXY8lYFOrSRs6\nEtPgYeDh4ejyRC6S0BZCCCe3bUFP1s89TTEjZD9fhdR5C7FUet7RZYk8IKEthBBOSpGQgGVoD97d\nvINMFSSNGoVlwHBwc3N0aSKPSGgLIYSzsdnw+HYdPqOGoUpKZF8JuPVBNDXqd3F0ZSKPSWgLIYQT\nUd78E82IIXhs/o4sDzXDXoHELp2YI4FdIEhoCyGEM7DZ8IhZg2bsaJQpt0h+sRq1ah/HWLIEP9ed\n5ujqxFMioS2EEPmc8uoVtMMG4f7jdqw+Gm5Nm0l9n884k2ThiwbRaN19HV2ieEqUji5ACCHEfVit\neK5cjn+9mrj/uJ2sBo1I/vlXplW+xW9Jv9GhQmcalYpwdJXiKXqoPe2pU6cSGxuLQqEgMjKSypUr\n2+dt376dRYsW4e7uTrNmzejYsSP79+9n0KBBlC1bFoBy5coxduxYbty4wYgRI7BYLOj1embNmoW7\nu3vedCaEEE5MeeE82qEDcd/zM1bfQtyet5DMdh04HH+IqMMzKe4TxMTaUxxdpnjKcgztAwcOcOnS\nJWJiYoiLiyMyMpKYmBgArFYrkyZNYv369fj5+dGjRw8iIu586gsLCyM6OvqudUVHR9O+fXuaNm1K\nVFQUa9eupX379nnQlhBCOCmLBa9li/GZ+l8UJhMZrzTlwMhufJu2n80xtfk96SQAcxrMw9ejkIOL\nFU9bjofH9+3bZw/i4OBgUlJSMBqNACQnJ+Pr64tOp0OpVFKzZk327t1733Xt37+fl19+GYCGDRuy\nb9++3OhBCCFcguqPs/g1fxXNmFFkuqtZNLgBZV4+Sv2fWxN1eBbnU84RUaoJHzdZycvPNHF0ucIB\nctzTTkhIIDQ01D6t0+kwGAxoNBp0Oh1paWlcvHiRoKAg9u/fT1hYGEFBQZw7d47evXuTkpJC//79\nCQ8PJz093X44PCAgAIPBkHedCSGEszCb8VwwD+9ZU1FlZfP182p6v3qbBJ9d+Fv8aRPyNq+Ufo2G\npV5G4yZDahZkj3z1uM1msz9WKBRMnz6dyMhItFotJUqUAKB06dL079+fpk2bcuXKFTp37sy2bdvu\nu5778ff3Rq1WPWqJuU6v1zq6hDwl/Tk3V+8PXLvHxF93Yu7SCe2Za9zQQN9W8FvtZ+gc0oLmIc0J\nLxWOWuncX/Rx5e33l6fVY44/CYGBgSQkJNin4+Pj0ev19umwsDDWrFkDwJw5cwgKCqJIkSK89tpr\nAJQqVYrChQtz8+ZNvL29ycjIwNPTk5s3bxIYGPjA905ONj1WU7lJr9diMKQ6uow8I/05N1fvD1yz\nR6vNyu4LP5A9Ywytvz2DmxU+q6ZkV99WdA/rzYtFw1AoFAAkJ6Y7uNon44rb759yu8cHfQDI8Zx2\neHg4W7duBeDkyZMEBgai0fx9eKZ79+4kJiZiMpnYuXMntWrVYsOGDSxbtgwAg8FAYmIiRYoUoXbt\n2vZ1bdu2jbp16z5RY0II4UyM2Uaij0TRbXoFyjV/i7fXnyGhkBtfTu1GrQ0Xmd5iBWHFXrIHthD/\nlOOedvXq1QkNDaVdu3YoFArGjx/PunXr0Gq1NG7cmDZt2tC1a1cUCgU9e/ZEp9PRqFEjhg0bxo4d\nO8jOzmbChAm4u7szYMAARo4cSUxMDMWLF6dly5ZPo0chhHAom83Gd+e/ZcrOUfTYdJ1v94LKBpfb\nvE7JJZ/RMEtumSEejsL2MCeXHSQ/HFJx9UM70p9zc/X+wPl7jLv1B6N3Dyfrlx9Z8S2US4TsUqVI\nm7uQ7Dr1nL6/nLh6f/B0D48799UNQgiRT5myTcw9PJsVB+Yy8QczAw6AAgWmnr1JGz0OfHwcXaJw\nQhLaQgiRi2w2G5svbGLMnpGUPX6F2O9UPJME5ufKkjp3IeawlxxdonBiEtpCCJFLrqVeZdhPgzh4\n9gdmb1fS4xDYVGAaOIS0YaPA09PRJQonJ6EthBC54EzSadpsbEnVo9f5Y7MHgcmZmCtWInXeAsxV\nqjm6POEiJLSFEOIJHb15mD5ftWLat7d4JxZsblbSRkRiGjgEZFAkkYsktIUQ4gnsufYzX81qzS8b\nMihqhOwq1UidtxBLxdCcFxbiEUloCyHEY/rx0GpUw/ux5qQVs7sbxrFjSe/TH9Typ1XkDfnJEkKI\nR2WzceTDwbw8ZwWFTZBQpTzKRauxPFfW0ZUJFyehLYQQj0B54zqJvVrxyq+/k+YGv4/qR+FBk7Go\nHD+4kXB9EtpCCPEwbDY81nyG25ihBKRlsifYHY+PvqB0lQhHVyYKELnhrRBC5EB55TIeb76K73v9\nyc7OJLJ1AJ5bDkpgi6dOQlsIIe7HaiVj0Uy8w6viu2cf3z8Hb46tQPvZv/JMoTKOrk4UQHJ4XAhR\nIJxJOs3Mg1Mpr6tA3aD6VC9SA3fV/b9DbTi+B+WArpT//U+SPWFs+0DK9P4vn5Zrg1opfzqFY8hP\nnhDC5SWmJ9Lh+zZcvn2RjXFwXZ0nAAAgAElEQVTfMOvgNLzUXoQVrUndEvUJD6pLFX011Eo111Mu\nc3pSV5qvOYCXGbY+7821ieMZWruHhLVwOPkJFEK4tGxLNt23duby7YsMrDaEF4q+yJ6rP7Hn2s/8\ndHUnP13dCYDGTUtLczn6Lz1C26s2EjRKdg3rStVeM6iucnNwF0LcIaEthHBpY34ZyS/Xd9Ps2eZE\n1hyHUqGkaZlmABhMBvZe383ei7sIXbWB/lsP42GBMy/XoNDc1dQoUszB1QtxNwltIYTL+uTEMlac\n+JiKAZWY//JHKBV3X3ur99bzRvpzvDM1CrcTSZgDA0maGYXuteYOqliIB5PQFkK4pF+u7SZyz3AC\nPAP4tOnnaNw0d78gMxPvD2biHf0BCrOZ9PadSJswGZufv2MKFuIhSGgLIVzOpdsX6ba1EwDLX11F\nKd9n7pqvPnwQ7eB+qM+cxlKiJKlzoslu+LIjShXikUhoCyFcijErlc7ftyMpI4nZ9edRq3j43zPT\n0/GZMQWvjz5EYbWS/m530sZOxKbROq5gIR6BhLYQwmVYbVb67ejF70mn6FqpB51D37XPc/t1L5rB\n/VCfj8NSugypcxeQXbuOA6sV4tHJHdGEEC5j5oEpbL7wHXWC6jEpfPqdJ41GNKOG4tf8VVQXzmPq\n3Z+kXfsksIVTkj1tIYRL+Pz3VUQdnsUzvqX5+JWVuKnccPtpJ9ohA1BduYy5XAipcxdgrhHm6FKF\neGwS2kIIp5ZuTmfMnlF8dmoFGjctn70WQ0CmCp/R/fFa/Sk2lYq094ZhGjISPDwcXa4QT0RCWwjh\ntM4knabnti78nnSK0IDnWdrkEyoePIdmWEtUf97AHPo8qdELMT9fxdGlCpErJLSFEE7HZrMRc2YN\no34eisls4t1K3ZkUMpSAyPF4fv0lNjc30kaNwTTgPXCTW5AK1yGhLYRwKsZsIyN/GsJXZ7/A170Q\ny175jDdP2dA2rIcywUB2teqkzluEpXwFR5cqRK6T0BZCOI3fEo7Tc1sX4m6do3rgCyyrNosKk+fi\nsWkDNk9PjOMnk96rL6jlT5twTQ/1kz116lRiY2NRKBRERkZSuXJl+7zt27ezaNEi3N3dadasGR07\ndgRg5syZHD58GLPZTK9evWjSpAmjRo3i5MmT+Pn5AdCtWzcaNGiQ+10JIVzOZ6c+IXL3cDItmfSp\n3J/JVyvi1/QNlLdukVWzNsYP5mMJLuvoMoXIUzmG9oEDB7h06RIxMTHExcURGRlJTEwMAFarlUmT\nJrF+/Xr8/Pzo0aMHERERXLx4kT/++IOYmBiSk5Np1aoVTZo0AWDIkCE0bNgwb7sSQriUhcfmM2Hv\n++g8dXxedS6vzVuPx/YPsXn7kDptNhnvdgel3HZCuL4cQ3vfvn1EREQAEBwcTEpKCkajEY1GQ3Jy\nMr6+vuh0OgBq1qzJ3r17adGihX1v3NfXl/T0dCwWSx62IYRwVVH7opiw932KeRdjT2Y3SrcfiTL1\nNln1GpIaFY211DM5r0QIF5FjaCckJBAaGmqf1ul0GAwGNBoNOp2OtLQ0Ll68SFBQEPv37ycsLAyV\nSoW3tzcAa9eupV69eqhUKgBWrVrFihUrCAgIYOzYsfbAvxd/f2/UatWT9vjE9HrXvi+x9OfcXLm/\nub/OZei2obyUFciPP5bG++fJ4OsLH3+Me9euBCgUji4xV7jyNgTX7w+eXo+PfLWGzWazP1YoFEyf\nPp3IyEi0Wi0lSpS467Xbt29n7dq1LF++HIAWLVrg5+dHhQoVWLJkCR9++CHjxo2773slJ5setbxc\np9drMRhSHV1GnpH+nJsr97ckdiFjd49iTKwvE7bdRpW+j8zGr2CcPQ9rseKQYHR0ibnClbchuH5/\nkPs9PugDQI6hHRgYSEJCgn06Pj4evV5vnw4LC2PNmjUAzJkzh6CgIAB2797NRx99xMcff4xWe6eA\nWrVq2Zdr1KgREyZMeLROhBAFwsfHP+LTb0ex7zs3Xrp4G6u/P7fnzCfzzTbgInvXQjyOHK/cCA8P\nZ+vWrQCcPHmSwMBANJq/B5Pv3r07iYmJmEwmdu7cSa1atUhNTWXmzJksXrzYfqU4wIABA7hy5QoA\n+/fvp2xZudJTCHG35ccWkjx9BLEfwUsXs+Gtt0jafZDM1m0lsEWBl+OedvXq1QkNDaVdu3YoFArG\njx/PunXr0Gq1NG7cmDZt2tC1a1cUCgU9e/ZEp9PZrxofPHiwfT0zZsygQ4cODB48GC8vL7y9vZk2\nbVqeNieEcC4bvp1Io/FzePE6ZAXoSJk5j0JdO2Jz8cOrQjwshe1/T1LnM/nhPIirn4+R/pyby/SX\nlcWZMR0I+3Qr7laIb/EayhkLsOkCXKfH+5D+nF++OqcthBB5yXx4H+beb1PnUhLXfZUkz5xN4Bvd\nybd7E0I4kIS2EMIxMjJI/e9gSi1fg9oKX9b2o9S89QQ/84KjKxMi35LQFkI8fb/+grVvB569msQF\nP9gwuAVv9FyKp9rT0ZUJka9JaAshnp60NLInDKHop5+jtMHyOhr0Mz6hfdkmjq5MCKcgoS2EeCpU\nu3eh6N8F/Y0kzupgzYAIOnVfga9HIUeXJoTTkNAWQuSt2ymkR/al1JcbsSggup4nfhMX0i+0taMr\nE8LpSGgLIXKdxWrh4J/7ubB2Pm9+uIVStyyc0MNHvV6id/dVFPEu4ugShXBKEtpCiFyRbcnml+u7\n2XR+I7+c+JbIbxMYeAyylfDVG6GYh4xmXNnXUchdzYR4bBLaQognYrPZmHNoBkuPLyI5M5nmp2HP\nJgVFUiE5pAxZC1bQoHJ1R5cphEuQ0BZCPDarzcro3cNYceJjylsKs/nHYF76JQ6buxvG90dj7jsQ\npZubo8sUwmVIaAshHovFamH4T4NZdWol710qwcwNJtRJcWS/8CKp8xZiKRfi6BKFcDkS2kKIR2a2\nmhn0Y192H/6CHT/40uj4VWxeXhgnTSO9e29QqRxdohAuSUJbCPFIsi3Z9NvenUJr13Nmmwrf9Ntk\n1a5DatR8rM8GO7o8IVyahLYQ4qFlWjJ5//N29Fqwg1fjwOrjSerMyWR0fheUSkeXJ4TLk9AWQjyU\njCwT60Y35MOY39FmQXqDBpiiFmAtUdLRpQlRYEhoCyFylPXHKRK6vsqgM7dI9VaTOGMO1vZdQL5z\nLcRTJaEthLg/iwXlR3MJmDqJoGwre6sVofSK7bgVf8bRlQlRIEloCyHuSXX2DN4De+F55AgGb5jf\nowbtx2zGTe3h6NKEKLAktIUQdzOb8VowD59Z01BkZfF5Jdja9z9Me+NT1Er5kyGEI8lvoBDCTnXi\nN7SD++F2/BgGXzU9WoFbi7ZEN1okgS1EPiDf0RBCQFYW3jOm4N+kPm7Hj/HNS/6U62PGq1UH5jf6\nSAJbiHxCfhOFKODURw+jHdwP9e+nyC5ejH4t3VkaeIlOFbswq/5clAr5bC9EfiGhLURBlZ6Oz8yp\neC2aj8JqJalDe16pfJhD6WfoEtqN6fXmSGALkc/Ib6QQBZD61334N6yN94J5WEuW4sLnn1Er7E5g\n93i+NzPqRUlgC5EPyW+lEAWJ0YhP5HD8WryK6sJ5TL36sfvrpTS+OZGzyWfoXaU/k+vMQCE3TREi\nX5LD40IUEG4/70I7ZACqy5cwly3HmcmjGZO9kW++awzAgGrvMabmBAlsIfIxCW0hXJzidgo+E8fi\n9dkn2FQqbvbpSWS4iZWnu2OxWaiir0bkS+NoWOplR5cqhMjBQ4X21KlTiY2NRaFQEBkZSeXKle3z\ntm/fzqJFi3B3d6dZs2Z07NjxvsvcuHGDESNGYLFY0Ov1zJo1C3d397zpTAiB+w9b0AwbjOrGdTIq\nlOeDbpWZmL6SzHOZlPUrx6iXxvKfZ5vL3rUQTiLH0D5w4ACXLl0iJiaGuLg4IiMjiYmJAcBqtTJp\n0iTWr1+Pn58fPXr0ICIigsuXL99zmejoaNq3b0/Tpk2Jiopi7dq1tG/fPs+bFMKVma1mEjMSMVuy\nybZmY7aasSUmUGZ6FPoNW7Gq1WxrX4e2IUe5ZTxNCU1Jhr84mrdC2sn3r4VwMjn+xu7bt4+IiAgA\ngoODSUlJwWg0otFoSE5OxtfXF51OB0DNmjXZu3cvV65cuecy+/fvZ+LEiQA0bNiQ5cuXS2gL8QSS\n0pNo9GUdTif9bn/ujVOwcBMUSYODxaFrCzMniuyhsGdhprwwjs6hXfFQyf3DhXBGOYZ2QkICoaGh\n9mmdTofBYECj0aDT6UhLS+PixYsEBQWxf/9+wsLC7rtMenq6/XB4QEAABoMhD1oSomCw2qy8s64j\np5N+p05QPcpl+9Fj5TFq7r9MtpuKrzvVYGeLGjRy86CDphhty3dA46ZxdNlCiCfwyMfGbDab/bFC\noWD69OlERkai1WopUaJEjss86Ll/8vf3Rq1WPWqJuU6v1zq6hDwl/TmnCbsmsPncZl4NfoVNdEQ5\najAkJkLt2rgtX86bISG86egic4mrbsO/SH/O72n1mGNoBwYGkpCQYJ+Oj49Hr9fbp8PCwlizZg0A\nc+bMISgoiMzMzHsu4+3tTUZGBp6enty8eZPAwMAHvndysumRG8pter0WgyHV0WXkGenPOf1wcQsT\nf5rIS5Tgq0/MKHd0wubtTdqUGaR37QkqFbhI3666Df8i/Tm/3O7xQR8Acry5Snh4OFu3bgXg5MmT\nBAYGotH8fYite/fuJCYmYjKZ2LlzJ7Vq1brvMrVr17Y/v23bNurWrftEjQlREF1IOU/f7T3odUzN\nL3Nuodmxg6w69UjatY/0Hn3uBLYQwiXluKddvXp1QkNDadeuHQqFgvHjx7Nu3Tq0Wi2NGzemTZs2\ndO3aFYVCQc+ePdHpdOh0un8tAzBgwABGjhxJTEwMxYsXp2XLlnneoBCuxJRtYszqtnz1aQqNzwNa\nBamz55HRqQvI17aEcHkK28OcXHaQ/HBIxdUP7Uh/zsNmsbBxdARtVx9Gkw2ZLzfGY8UyDJ5+ji4t\nT7nSNrwX6c/55avD40IIx1OdP0dmkxfo9slhLG4qkqIXcHvNWihZ0tGlCSGeIrmzghD5mcWC1+KF\neE2biC4zi+9C3Sm97AeKPFvN0ZUJIRxA9rSFyKdUp3/Hr1kEmgnvk6w207aNgqxP10pgC1GASWgL\nkd9kZ+MdNRP/iLq4HTnMtjA95ftaCek2kbolGzi6OiGEA8nhcSHyEfVvsWgG9cPtxHHS9P70+4+G\nlc8YaPZsc/pXHeTo8oQQDiahLUR+kJmJd9QMvKM/QGGxsLluCd6ufRWTjxtDqo9gcPVhMhKXEEJC\nWwhHUx8+iHZQX9Rnz5Ac6Een10xsKn2VOkH1mFEvirL+5RxdohAin5DQFsJRTCZ8ZkzBa/ECFFYr\nq+v607tOMp5+hVlQeyqty7WVvWshxF0ktIVwALe9e/B5rx9uFy7wZ1EtbV5NZXfpZDpX7MqYmuPx\n8/R3dIlCiHxIQluIp8Bms3E+5RzHL+zhuQ8W02jLKSwKmFUbxjdIpUyxSmyq/wEvFn3J0aUKIfIx\nCW0h8tDGuG9ZdeoTjsYfpsapWyzdAKVT4JQepncJwb1mfeYVrcV/glugVsqvoxDiweSvhBB5ZOnx\nRby/ZySF0mHxTg1tD4BVqeRcz7fRjp7OHJ9Cji5RCOFkJLSFyGU2m425h2cz7cAkOl0oxNLNbnjE\nJ5BdqTLGeQso9HwVR5cohHBSEtpC5CKbzcbkXyewZs8HrNvuTaujKdjc3UkbPRZT/8Hg5uboEoUQ\nTkxCW4hcYrVZGfXTEIxfLefMZhUBRhPZ1V8gde5CLOUrOLo8IYQLkNAWIheYrWbGrXuX/8z/ljd/\nB6uHGuPESaT37AMqlaPLE0K4CAltIZ5QpjmDLye8woxPj6LLAFNYGBnRH2F59jlHlyaEcDES2kI8\ngcyLf3CtWxOG/JaIyUNJwpRJ2Lr1A6UMoCeEyH0S2kI8BpvVyo0PxxI8ewElMqwcDg2g6PItuJcJ\ncXRpQggXJrsDQjwCq83KT7uXcbF+SapMno/ZZmVhjxoU/eG0BLYQIs/JnrYQDyHTksna3z8ndf4k\nhnxnwCcbfq0aiHHWPN6q0szR5QkhCggJbSEeIDXrNitPrmDH9mimf2GgzhVI1XpwetoYgjsNBBmF\nSwjxFEloiwIr3ZzOvut7SEhPICkjkcT0xLv+TcpI5Maty/TZnc72XeBphluvvYp51gIC9HpHly+E\nKIAktEWBlJyRROsNLfgtIfae8xUoqH1Ly9qvbTx/Bcx6PSnTo8h+vcVTrlQIIf4moS0KnP8N7BbB\nb1C/ZEN0ngHovAII8AxAp9QStHgFmgVzUGRnk9G6LcbJ07HpAhxduhCigJPQFgVKckYSb21syW8J\nsXSq2IVZ9eeiVPz9JQp17FG0g7qgPnUCS7HiGGfPJavxqw6sWAgh/iahLQqMvwL7uOEYHSu8c3dg\nZ2TgM3s6XgvmobBYSO/UhbTxk7D5yvCZQoj846FCe+rUqcTGxqJQKIiMjKRy5cr2eatXr2bDhg0o\nlUoqVarE+++/z6JFi9i7dy8AVquVhIQEtm7dSqNGjShatCiq/78X8+zZsylSpEgetCXE3W5lJN8V\n2LMbzLMHtvrAfrSD+6I+9weWUs+QGjWf7HoNHFuwEELcQ46hfeDAAS5dukRMTAxxcXFERkYSExMD\ngNFoZNmyZWzbtg21Wk3Xrl05duwYffr0oU+fPgCsX7+exMRE+/qWLl2Kj49PHrUjxL/dN7DT0vCZ\nPgmvJYsAMPXoTdrocaDROLhiIYS4txxDe9++fURERAAQHBxMSkoKRqMRjUaDm5sbbm5umEwmvL29\nSU9Pp1Chvw8nms1mPv/8cz799NO860CIB0hOvxPYsYajdKjQ2R7Ybnt+Rvtef1SXLmIOfo7UDxZg\nrlnL0eUKIcQD5Xgb04SEBPz9/e3TOp0Og8EAgIeHB/369SMiIoKGDRtSpUoVypQpY3/ttm3bqFOn\nDp6envbnxo8fz9tvv83s2bOx2Wy52YsQd7mVkUyTVU3sgT2nQTQqoxHN8Pfwe+M/KK9cxtRvEMk/\n/iKBLYRwCo98Idr/Bq3RaGTx4sVs2bIFjUbDO++8w+nTpylfvjwAX3/9NRMnTrS/fuDAgdStW5dC\nhQrRr18/tm7dyquv3v/KXH9/b9Rqx49FrNdrHV1CnnLF/lIzU+nwTWsOXT9E16pdWdp8Kcqt26Bn\nT7hyBSpVQrF8Od4vvoi3o4t9Qq64/f7J1XuU/pzf0+oxx9AODAwkISHBPh0fH4/+/+8GFRcXR8mS\nJdHpdADUqFGDEydOUL58eUwmE3/++SclSpSwL9uyZUv743r16nH27NkHhnZysunRO8pler0WgyHV\n0WXkGVfsL9OSSftNb3Hw+kHeqfIO08qPJevtTnjGrMGmVmMaNgrT4GHg7g5O3rsrbr9/cvUepT/n\nl9s9PugDQI6Hx8PDw9m6dSsAJ0+eJDAwEM3/X6gTFBREXFwcGRkZAJw4cYLSpUsDcPr0aZ599ln7\nelJTU+nWrRtZWVkAHDx4kLJlyz5eR0Lch8Vqoe/2Huy+uotXyzRjmfV1AurVxDNmDdmVq5K87SdM\nIyLvBLYQQjiZHPe0q1evTmhoKO3atUOhUDB+/HjWrVuHVqulcePGdOvWjc6dO6NSqahWrRo1atQA\nwGAw2PfAAbRaLfXq1aNt27Z4eHhQsWLFB+5lC/GobDYbo3YPY2PcNzTVhvHV12pUG1pj8/DAOGYC\n6X0HglpuTSCEcF4KWz6+Giw/HFJx9UM7rtTf9AOTiTo4k2GXSjJ9QxqqpCSoVYukWdFYyrnmWNeu\ntP3ux9V7lP6c39M8PC67HcIlLD2+iM9/nMnWbd40OXEFm5cXxknT0IwejiXJ8ddGCCFEbpDQFk7v\n6zMxnJ0/klPbFPilm8gKr0tq1HysZZ5Fo3L8tw+EECK3SGgLp/brgTWUGdyH3ufA7ONF6qypZHTq\nAsocr7EUQginI6EtnJPVys0Px9FgZjTaLIgPr4Fq/kqsJUo6ujIhhMgzsjsinI7yfBy2ZuFUmhyN\nWQl7x/VFsW6HBLYQwuXJnrZwHhYLHksW4DllAu5ZZr6toCB56gyahfd2dGVCCPFUSGgLp6A6ewaP\nAd3xORqLwRsmtNPTcviX1C7ygqNLE0KIp0ZCW+Rv2dl4LYzGa+YUVNlm1lSC7/s0ZWLzJfh6FMp5\neSGEcCES2iLfUp34Dc2gvrj/Fst1DQx8S01Y95lEhXZDoVA4ujwhhHjqJLRF/pOZifcHs/COjkJh\nNrOiKkS/VZo5rVbxfOHKjq5OCCEcRkJb5Cvqo4fRDuqL+vTvXCmkoPvroGn6Fuvqz0Xj7vrD+wkh\nxINIaIv8IT0dn5lT8Vo0H4XVyqIaMP4VdyIbz6F9hU5yOFwIIZDQFvmA+td9aAf3RX0+jj8DfWjX\nNI2zlYqzuukaqgZWd3R5QgiRb0hoC8cxGvGZOhGvZUsAWNUokF4146lQsgbbXl1DEZ+iDi5QCCHy\nFwlt4RBuP+9CO2QAqsuXMJYpRbvX0tikj6dNyNvMrj8PT7Wno0sUQoh8R0JbPFWK2yn4TBiD16qV\n2FQqjnRqSsMyOzCqzEyoNYU+VfrL+WshhLgPCW3x1Lj/sAXNsMGoblwnu2Ioc7tVYUTqGrTuvqxu\nvJyXn2ni6BKFECJfk9AWeU6RlIhmzCg818ZgUatY36Y6kWEpnE5dw7OFgvnstRjK+pdzdJlCCJHv\nSWiLPHPDeJ0ba+ZRc9YKPFMyOFAcurawcLLIEbwzvGn13JvMqBeFn6e/o0sVQginIKEtco3VZuXI\nzUN8f+E7Dh7/lqGfX+CtU5Chgvdfdefgm3VpVbIes4qHU0VfDTeVm6NLFkIIpyKhLZ5ItiWbX67v\n5vvzG9ly8Xv+NN6g/W+waTMEpMPl0FJcnjaJ/mGvo1bKj5sQQjwJ+SsqHpnVZmXrxc1sjPuGHy5t\nJSXzFgChmX58tzWIF45cw+rlhXHKBLy69SJEqXRwxUII4RoktMUjSctOY8CO3nx3/lsAgjQleKts\nG/rEelD1w09Qpl4jq259UqPmY32mtGOLFUIIFyOhLR7adeM1On3fjt8SYqldvA4Tak+mWroO36GD\ncP95J1atL6lzosno+A7Id62FECLXyXFL8VCO3DxEk7UN+C0hlk4Vu/Bls3XU3HiQgPq1cP95J5kR\nTUjevZ+MTl0ksIUQIo/InrbI0fo/1jLox75kWbOYFD6NPj5N0L7ZEvdf92L18yN11hIyW7eVsBZC\niDwmoS3uy2qzMuvgNOYcmoHGTcsnjVfSbPMf+MwIR5GRQeZ/WpA6bTa2IkUcXaoQQhQIEtrinkzZ\nJgb82JuNcd9Qyrc068pOo3LfmbgdOYy1sJ7bHy4mq3krR5cphBAFykOF9tSpU4mNjUWhUBAZGUnl\nypXt81avXs2GDRtQKpVUqlSJ999/n3Xr1jFv3jxKlSoFQO3atenTpw+nT59mwoQJAISEhDBx4sTc\n70g8sT/TbtDp+3bEGo5SJ7AW6+JqUXhkZxTZ2WS82Qbj5BnYAgIcXaYQQhQ4OYb2gQMHuHTpEjEx\nMcTFxREZGUlMTAwARqORZcuWsW3bNtRqNV27duXYsWMAvPbaa4wcOfKudU2ZMsUe+kOHDuWnn36i\nfv36edCWeFyZlkw6ft+W44ZjRHo2Y/yCS7ifjMJStBjG2XPJatLU0SUKIUSBlePV4/v27SMiIgKA\n4OBgUlJSMBqNALi5ueHm5obJZMJsNpOenk6hQoXuuZ6srCyuXbtm30tv2LAh+/bty60+RC6ZsPd9\nTt84xrrYSkx+fwvuJ0+Q3vEdknfvl8AWQggHy3FPOyEhgdDQUPu0TqfDYDCg0Wjw8PCgX79+RERE\n4OHhQbNmzShTpgxHjx7lwIEDdOvWDbPZzMiRIwkICMDX19e+noCAAAwGwwPf29/fG7Va9QTt5Q69\nXuvoEvLUX/2tPbWWE98v4dQmD4L/PAHPPANLl+LVuDFeDq7xSRSU7efKXL1H6c/5Pa0eH/lCNJvN\nZn9sNBpZvHgxW7ZsQaPR8M4773D69GmqVKmCTqejQYMGHD16lJEjR/Lxxx/fdz33k5xsetTycp1e\nr8VgSHV0GXnmr/4u/XmSG307sPcXUNoySe/aA+OYiaDRgBP3X1C2nytz9R6lP+eX2z0+6ANAjqEd\nGBhIQkKCfTo+Ph69Xg9AXFwcJUuWRKfTAVCjRg1OnDhB69atCQ4OBuD/2rv3uKjq/I/jr2FmGC6D\nyCiggi5qCirJ4mIXTRQCy/RntZVpKZr4M0XItITEC5rlLTM1r6GuZqSuSK2pBT8X6+cvCbM1DcxU\ntpIuotyUARRmOL8/fDRpKgKrMwx8nn85M+ccP2+/nvOZc75nZoKDgykuLsbDw4PS0lLLdgoKCvDy\n8mpYInFbKQcy8Xp+GHGFVZT6eMKaLVTf18fWZQkhhPiDW85p9+3bl/T0dAByc3Px8vJCr9cD4OPj\nQ15eHpcuXQIgJycHPz8/kpOT2b17NwAnT57EYDDg6OhIp06dOHz4MAAZGRn069fvjoQSdaMylkFM\nDF5PPIZPURW7h3Sn+vNvpGELIUQjdcsz7V69etGjRw+GDx+OSqUiKSmJtLQ03NzciIyMJDo6mqio\nKNRqNcHBwYSEhODr68u0adPYtm0bJpOJ119/HYDExERmz55NTU0NQUFB9OkjzcFWtJn7cHt5MvyU\nT64nvDrKj8UvZYLWxdalCSGEuAmVUpfJZRtpDPMgTW0+RlVagmvSDJy3vkeNRsOSfg4s6K9h9/DP\n6Grwt3V5t11TG78/aur5oOlnlHz2r1HNaYumw/GTveinvYi64CxVgYGMHFLFDqeTrHpwZZNs2EII\n0dRI024GVIWF6GfG45SWiuLoSHnibKYG/cKOb9cTHRzNU/7DbV2iEEKIOpCf5mzKFAXdhzsx9OuN\nU1oq1X8JoSAjk3cGesHCylEAABRPSURBVPLOt+vpZujOikErbF2lEEKIOpIz7SbKoeAs+oSX0O39\nCLPOkfTxg1hyTxUH/28gFaYKXDSurH/oXVy0LpTTtOebhBCiqZCm3dQoCpVbVuM1dx66sgoOdtQw\nekgVp1t9DD+Bv0cAob4DeDrgGbp4dLV1tUIIIepBmnYTouT/SMnzj+N/+DRGLcQ8Ah+EtqJfhzBe\nbB9GqO8A2ri2tXWZQgghGkiadlNQU8Pl9cvweG0eXpfMfNbFkW9mv8gzvZ9kjoc/KpXK1hUKIYS4\nDaRp2zmHH76neuIz+H6VS6kO3hp7N4Nm/4PuLq1tXZoQQojbTJq2vTKb0SSvxOX1uegum9jt78CP\n82bybP+X5MxaCCGaKGnadkh96iTq2LG4HzlGoTMkjm7H0IRUhrUOtHVpQggh7iBp2vbEZMJ59Qqc\nFr2GptrE9h7w+ZRnePmRt3DW2PMvXgshhKgLadp2Qn08F/0LE3A8dpSzrhA/zJUH45KZ1WmIrUsT\nQghhJdK0G7uqKlyWv4nLsiWoqqvZHAQbn72bFU/+nXZ6H1tXJ4QQwoqkaTdimq//hdvkSWi+zeVs\nSy3PDYaaiIfZPPBvuGpdbV2eEEIIK5PvHm+MLl3CdV4SLR8OR/NtLlvuc6XrhGq8H4tm06D3pWEL\nIUQzJWfajYzmUDZuL8agOX2Kch9vhj9sZHf7cmbeN4e44CnycS4hhGjGpGk3FuXluC54FefktQAc\neyqCUP9PqXBUsTo8mSe7Pm3jAoUQQtiaNO1GQHvgM9ymxKE+8wOmu7qwccIDPG/8Gy0c3dk+KIUH\nfEJtXaIQQohGQJq2DanKLuI6dzbO725EcXCgPG4KL/W5wLrvNuKj9+X9wal0a9Xd1mUKIYRoJORG\nNBtx/GcGHv3uxfndjZi69aD4438ysV8J677bSDdDd/b+dZ80bCGEENeQpm1lqpJi3OIm4D7iSRzO\nFVA+bTqF6ZnElqxny/FN3N06iA8e20NbfTtblyqEEKKRkcvj9WCsKuPQ2S8wOLXC26UNni5eaBzq\n/k/ouOcj9AlTUZ8roDoomLJlq7jcLYAXMieSenI7wV692D7kA1o6edzBFEIIIeyVNO06UhSFifvG\nkf7Dx5bnVKho5dwab5c2eLt64+3Shrb6dgzp9CiBre/+fbnz59EnTsPpH2koOh3GmXOojHmBapVC\n7L7/5oPTO/mLd2+2D0mjhc7dFvGEEELYAWnadbQr7wPSf/iYP3sGc2/b+ymoOEtBRQEF5Wf54eL3\n5BZ9Y1l26eHF9PcNIyYojocOl+A2YxoOxcVU976XsuWrMd/VhSpzFRP+J5rd//4H97a9n/cH78DN\nsYUNEwohhGjspGnXQcmlYqYfmIaT2om1AzfSyb3zdcsYq42cKz/Lt8XfsuGbdZw8vh/dG/tx/w6q\nnRy5OG8+1eMmglrNZfNl/jtjDJ98v4e+7fqxZfB29Fq9DZIJIYSwJ9K062DuwVkUVp5n5n1zb9iw\nAfRaPfqWd9HJvTNPfFGKU/K/0JYZ2d8Rov+rikqntxl3tJqnA55hSuYk9p3JINQ3jHcHbcVF62Ll\nREIIIeyR3D1+C5nfZ/L+iS30aHU3E4Nia13WIf8M7sMew+3FSagVFWVvLKNlxjc8FBZLWVUZr32R\nRM9NXdl3JoPwDhFseWSbNGwhhBB1Vqcz7fnz53P06FFUKhWJiYn07NnT8lpKSgq7du3CwcGBwMBA\nZsyYgclkYsaMGZw5cwaz2Ux8fDwhISGMGjWKiooKXFyuNKqEhAQCAwPvTLLboNJUyfiPxuOgcuCt\nsLfRqrU3XrCmBqdNG3Cdl4RDuZGq8AjKliynxrc9vsCrfefzUkg8W45vZlPOenp6/pnVEck4aZys\nmkcIIYR9u2XTPnToED/++CPbt28nLy+PxMREtm/fDoDRaGTDhg1kZGSg0WgYO3YsX3/9NXl5eTg7\nO7N161ZOnTrF9OnTSU1NBWDBggV07dr1zqa6Td78chF5JXlMCIrlz169briMw7/zcJsSi2PW59S4\nt+Ti22u5PGwE/OGHPdx1LYkNnkxs8GRrlC6EEKIJumXTzsrKIiIiAoDOnTtz4cIFjEYjer0erVaL\nVqu1nD1XVlbi7u7O0KFDGTJkCAAGg4HS0tI7m+IOyCn8hlVfL8evpR8J98y4fgGzGed31uC6cB6q\nykouDxqCcfFSarzbWL9YIYQQzcItm3ZhYSE9evSwPDYYDJw/fx69Xo9Op2PSpElERESg0+kYPHgw\nHTt2vGb9zZs3Wxo4wIoVKygpKaFz584kJibi5HTzS8QeHi5oNOqG5PqPmGvMxH84GbNiZu3gtfi1\n+0MjPn4cxo6F7Gxo3Ro2bUL31FPo7PRnMz093Wxdwh0l+exfU88o+eyftTLW++5xRVEsfzYajaxb\nt45PPvkEvV7P6NGjOXHiBAEBAcCV+e7c3FzWrr3yc5NRUVH4+/vToUMHkpKSSElJITo6+qZ/V0lJ\nRX3Luy3WHl3J4V8O82TXp3noroc4f77sygvV1bisXIbLm4tQVVVx6a9PYnxtMUrr1lBotEmt/ylP\nT7ff8zVBks/+NfWMks/+3e6Mtb0BuGXT9vLyorCw0PL43LlzeHp6ApCXl0f79u0xGAwAhISEkJOT\nQ0BAADt27CAzM5PVq1ej1V65gSsyMtKynfDwcPbu3duwRHfQmYs/sjD7NQxOBl7tu8DyvPqbY7hN\njkGbcwyzdxuMi9+iatBgG1YqhBCiubnlR7769u1Leno6ALm5uXh5eaHXX/kiEB8fH/Ly8rh06RIA\nOTk5+Pn5kZ+fz7Zt21i5ciU6nQ64coY+ZswYLl68CEB2djZdunS5I6EaSlEUpn32IhWmCub1XUhr\n59Zw+TIuC1/D46EBaHOOcWn4s5QcyJaGLYQQwupueabdq1cvevTowfDhw1GpVCQlJZGWloabmxuR\nkZFER0cTFRWFWq0mODiYkJAQli5dSmlpKePHj7dsZ8OGDQwbNowxY8bg7OyMt7c3cXFxdzRcfe08\n9Xf25/+TsPYP8mTXp9H86zC8FIdrbi5mH1/K3lxBdXiErcsUQgjRTKmUqyepGxlrzoMUVhbSb2tv\nKk2V/O9jn9JtTQrOa95GVVND5ZhoymfNRXFret8N3tTnmySf/WvqGSWf/WtUc9rNxYwD0yi6VMSm\nFuMJGjoCzb/zMPt1RL3pbxi73/gz2kIIIYQ1SdMGPv5+Dxm5O9mW5cXTn76DolJRMSGW8ldm4vkn\nb2ji7xKFEELYh2bftC9cLuWj9THk7AC/0nOYunSlbNkqTL3vtXVpQgghxDWaddNWXbxA/vhwdmSW\nYHZQUf7iS1RMjYdavvBFCCGEsJVm27QdMz5GOzWGsHNFfOfjhGHjXggOsXVZQgghxE01u5/mVBUX\n4TZxHO4jn0ZTVERSuAO/7PlYGrYQQohGr1k1bcc9H2F44B6cdv6d7+/ypNd4KJsylcB2f7F1aUII\nIcQtNZumrTKW0SJ6FCpjGblTxtFlxHmqA/yZGpJg69KEEEKIOmk2c9qKq56L726lvOOfGHroWWou\nqHgrbCU6tc7WpQkhhBB10mzOtFGpqBo4iPnnt/LvC3mMD4qhdxv5WJcQQgj70XyaNnCk4CvWHH2b\nP7XwY/o9s2xdjhBCCFEvzaZp1yg1vLg/lhqlhrfCVuKidbF1SUIIIUS9NJumXWmq5Gz5LzzfM4YH\nfEJtXY4QQghRb83mRjRXrSu5z+WhVqltXYoQQgjRIM2maQNoHJpVXCGEEE1Ms7k8LoQQQtg7adpC\nCCGEnZCmLYQQQtgJadpCCCGEnZCmLYQQQtgJadpCCCGEnZCmLYQQQtgJadpCCCGEnZCmLYQQQtgJ\nadpCCCGEnZCmLYQQQtgJlaIoiq2LEEIIIcStyZm2EEIIYSekaQshhBB2Qpq2EEIIYSekaQshhBB2\nQpq2EEIIYSekaQshhBB2QmPrAqxt/vz5HD16FJVKRWJiIj179rS8lpKSwq5du3BwcCAwMJAZM2Zg\nMpmYMWMGZ86cwWw2Ex8fT0hICKNGjaKiogIXFxcAEhISCAwMtFWsa9Q3Y1paGsuXL6dDhw4A9OnT\nh4kTJ3LixAnmzJkDgL+/P3PnzrVFnOvUN9+aNWs4ePAgADU1NRQWFpKenk54eDht2rRBrVYDsGTJ\nEry9vW2S6Wq15du3bx9r1qzB0dGRwYMHM3LkyJuu8+uvvxIfH4/ZbMbT05M33ngDR0dHW8WyaEi+\nxYsX89VXX2EymXj++ecZOHAgr7zyCrm5ubRs2RKA6OhoBgwYYItI16lvxuzsbCZPnkyXLl0A6Nq1\nK7NmzWoyY7hjxw527dplWSYnJ4cjR4406uPoyZMniYmJYcyYMZb/h785ePAgS5cuRa1WExoayqRJ\nkwAr7YdKM5Kdna2MHz9eURRFOX36tDJs2DDLa2VlZUpYWJhSXV2tKIqiPPfcc8qRI0eU1NRUJSkp\nSVEURTl58qTyxBNPKIqiKCNHjlS+++476waog4Zk3Llzp7Jw4cLrtjVy5Ejl6NGjiqIoytSpU5VP\nP/3UCglq15B8V0tLS1OSk5MVRVGUsLAwxWg0Wqnyuqktn9lsVkJDQ5WioiLFbDYrY8eOVX799deb\nrvPKK68oe/fuVRRFUd58800lJSXFymmu15B8WVlZyrhx4xRFUZTi4mKlf//+iqIoSkJCgpKZmWn1\nDLfSkIxffPGFEhcXd922msoY/nH9OXPmKIrSeI+j5eXlysiRI5WZM2cqW7Zsue71QYMGKb/88oti\nNpuVESNGKKdOnbLaftisLo9nZWUREREBQOfOnblw4QJGoxEArVaLVquloqICk8lEZWUl7u7uDB06\nlOnTpwNgMBgoLS21Wf110ZCMN1JVVcXPP/9seQcdFhZGVlaWdULU4j/JZzKZ2Lp163XvmhuT2vKV\nlJTQokULDAYDDg4O3HfffRw8ePCm62RnZ/Pggw8C9jF+N8vXu3dvli9fDkCLFi2orKzEbDbbLMOt\nNCTjzTSVMbzaqlWriImJsXrd9eHo6EhycjJeXl7XvZafn4+7uztt27bFwcGB/v37k5WVZbX9sFk1\n7cLCQjw8PCyPDQYD58+fB0Cn0zFp0iQiIiIICwsjKCiIjh07otVq0el0AGzevJkhQ4ZY1l+xYgXP\nPvsss2fP5tKlS9YNcxMNyQhw6NAhoqOjGT16NMePH7fsfL9p1aqVZTu21NB8ABkZGTzwwAM4OTlZ\nnktKSmLEiBEsWbIEpRF8OWBt+QwGA+Xl5fzwww9UV1eTnZ1NYWHhTdeprKy0XIazh/G7WT61Wm25\nfJqamkpoaKhlSuO9994jKiqKKVOmUFxcbP1AN9CQjACnT59mwoQJjBgxgs8//xygyYzhb44dO0bb\ntm3x9PS0PNcYj6Majeaa48TVzp8/j8FgsDz+Lb+19sNmN6d9tasP0kajkXXr1vHJJ5+g1+sZPXo0\nJ06cICAgALgyV5qbm8vatWsBiIqKwt/fnw4dOpCUlERKSgrR0dE2yVGbumQMCgrCYDAwYMAAjhw5\nQkJCAuvXr7/pdhqT+ozhzp07r5mXf+GFF+jXrx/u7u5MmjSJ9PR0Hn74YatnqM3V+VQqFQsXLiQx\nMRE3Nzd8fX1vuU5tzzUG9cm3b98+UlNT2bhxIwCPPvooLVu2pFu3brzzzjusXLmS2bNnW7X+uqhL\nRj8/P2JjYxk0aBD5+flERUWRkZFx0+00JvUZw9TUVB5//HHLY3s5jjbEndoPm9WZtpeX1zXv+s6d\nO2d5x5eXl0f79u0xGAw4OjoSEhJCTk4OADt27CAzM5PVq1ej1WoBiIyMtNy4FR4ezsmTJ62c5sYa\nkrFz586WG3iCg4MpLi7Gw8PjmqmAgoKCG14qsraGjmFFRQVnz5695iDy2GOP0apVKzQaDaGhoY1i\nDGvLB3DPPffw/vvvs27dOtzc3PDx8bnpOi4uLpYzF3sYP7hxPoADBw6wdu1akpOTcXNzA+D++++n\nW7dugP3sg3DjjN7e3jzyyCOoVCo6dOhA69atKSgoaFJjCFcu9wcHB1seN9bjaG3+mP+3cbHWftis\nmnbfvn1JT08HIDc3Fy8vL/R6PQA+Pj7k5eVZ/nFzcnLw8/MjPz+fbdu2sXLlSstlckVRGDNmDBcv\nXgSu/Ef87a5PW2tIxuTkZHbv3g1cuWPyt6bXqVMnDh8+DFy5tNyvXz8bJLpWQ/IBnDhxgk6dOlm2\nU1ZWRnR0NFVVVQB8+eWXjWIMa8sHMG7cOIqKiqioqGD//v3cf//9N12nT58+luftYfzgxvnKyspY\nvHgx69ats9wpDhAXF0d+fj5gP/sg3Djjrl272LBhA3Dl8mtRURHe3t5NZgzhSsNydXW1XCpuzMfR\n2vj6+mI0Gvnpp58wmUzs37+fvn37Wm0/bHa/8rVkyRIOHz6MSqUiKSmJ48eP4+bmRmRkJNu2bSMt\nLQ21Wk1wcDDx8fEsXbqUPXv20K5dO8s2NmzYwL59+1i/fj3Ozs54e3vz+uuv4+zsbMNkv6tvxrNn\nzzJt2jQURcFkMlk+qnD69Glmz55NTU0NQUFBlhvybK2++QDS09M5ePDgNZfHN2/ezIcffohOp6N7\n9+7MmjULlUplq1gWteXLyMhg1apVqFQqxo4dy9ChQ2+4TkBAAOfOnSMhIYHLly/Trl07FixYYLlS\nZEv1zbd9+3befvvta+5PWLRoEWfOnOGNN97A2dkZFxcXFixYQKtWrWyY7Hf1zWg0Gnn55Ze5ePEi\n1dXVxMbG0r9//yYzhnDlTfSyZcuumXrbu3dvozyO5uTksGjRIn7++Wc0Gg3e3t6Eh4fj6+tLZGQk\nX375JUuWLAFg4MCBlkv61tgPm13TFkIIIexVs7o8LoQQQtgzadpCCCGEnZCmLYQQQtgJadpCCCGE\nnZCmLYQQQtgJadpCCCGEnZCmLYQQQtgJadpCCCGEnfh/perTv1sN47gAAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "nunSIT7uVCft",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ ""
+ ],
+ "execution_count": 0,
+ "outputs": []
+ }
+ ]
+}
\ No newline at end of file