diff --git a/First_Date_with_TensorFlow.ipynb b/First_Date_with_TensorFlow.ipynb
new file mode 100644
index 0000000..124585a
--- /dev/null
+++ b/First_Date_with_TensorFlow.ipynb
@@ -0,0 +1,910 @@
+{
+ "nbformat": 4,
+ "nbformat_minor": 0,
+ "metadata": {
+ "colab": {
+ "name": "First_Date_with_TensorFlow.ipynb",
+ "version": "0.3.2",
+ "provenance": [],
+ "include_colab_link": true
+ },
+ "kernelspec": {
+ "name": "python3",
+ "display_name": "Python 3"
+ }
+ },
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "view-in-github",
+ "colab_type": "text"
+ },
+ "source": [
+ " "
+ ]
+ },
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
\n",
+ "\n",
+ "You know what's important for understanding Deep Learning / Machine Learning?
\n",
+ "Intuition. Period.\n",
+ "\n",
+ "And Intuition comes when you run the code multiple times.\n",
+ "\n",
+ "So, today I can write a couple of defination and say this is this, this is that.
\n",
+ "You Google half of the things up. You find answers which you need to Google further.
\n",
+ "In the process, you probably won't even remember what's the first thing you started out with!\n",
+ "\n",
+ "So?\n",
+ "\n",
+ "Hence on, I will execute cells with code.
\n",
+ "The neurons in your brain will optimize a function to get a hold of what each function is doing.
\n",
+ "**No Theory Just Code.**\n",
+ "\n",
+ "I will at max give a defination that extends for a line. That's it.
\n",
+ "Let's get started!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "**RECOMMENDED!**
\n",
+ "Write the code in the cells using the signals sent by your brain to your fingers!
\n",
+ "Don't just `shift+enter` the cells.\n",
+ "\n",
+ "[Source](https://github.com/iArunava/TensorFlow-NoteBooks)"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "gYWUpE-bYKWP",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Essential imports\n",
+ "import numpy as np\n",
+ "import tensorflow as tf\n",
+ "import matplotlib.pyplot as plt"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "eKpz5NCIYMdi",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define some tensors\n",
+ "t1 = tf.constant(2.0, dtype=tf.float32)\n",
+ "t2 = tf.constant([1.0, 2.0], dtype=tf.float32)\n",
+ "t3 = tf.constant([[[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]], \n",
+ " [[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]]])"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "vmMcjzTxbWzw",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "52d83a28-040a-4725-9f6b-03d865e533de"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's print them out!\n",
+ "print (t1)\n",
+ "print (t2)\n",
+ "print (t3)"
+ ],
+ "execution_count": 3,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Tensor(\"Const:0\", shape=(), dtype=float32)\n",
+ "Tensor(\"Const_1:0\", shape=(2,), dtype=float32)\n",
+ "Tensor(\"Const_2:0\", shape=(2, 3, 2), dtype=float32)\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "10ahnfjYbcop",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Where's Waldo?
\n",
+ "I mean, the value?
\n",
+ "\n",
+ "So, the thing is you can't print the value of tensors directly.
\n",
+ "You have to use `session`, so let's do that!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "ol6O5I7Tb2nb",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 204
+ },
+ "outputId": "fcc84119-a778-4e9d-997a-ed89b7c60e5b"
+ },
+ "cell_type": "code",
+ "source": [
+ "sess = tf.Session()\n",
+ "print (sess.run(t1))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t2))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t3))\n",
+ "sess.close()"
+ ],
+ "execution_count": 4,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "2.0\n",
+ "=======================\n",
+ "[1. 2.]\n",
+ "=======================\n",
+ "[[[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]\n",
+ "\n",
+ " [[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "rXKfVs_zb-kU",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Aaahaa!! Just printed those tensors!!!
\n",
+ "Feels good!
\n",
+ "\n",
+ "For some of you, who are like, dude you got \"No Theory Just Code\" in bold
\n",
+ "And you are still using the markdown cells for the theory ?!\n",
+ "\n",
+ "I am just gonna say I am a unreasonable man.
\n",
+ "\n",
+ "\n",
+ "So, you are programming with tf.
\n",
+ "What ever you do is broken down to 2 basic steps:\n",
+ "- Building the computational Graph!\n",
+ "- Execute that graph using `session`!\n",
+ "\n",
+ "That's all!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Let's compare this 2 steps with what we did above!
\n",
+ "So, I defined 3 `tensor`s and these 3 `tensor`s formed my computational Graph.
\n",
+ "And then I executed each tensor in this graph using a `session`.\n",
+ "\n",
+ "That simple!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Now, let's define a few more computational graphs and execute them with sessions.\n",
+ "\n",
+ "Okay, to start with let's build this computational graph!\n",
+ "\n",
+ "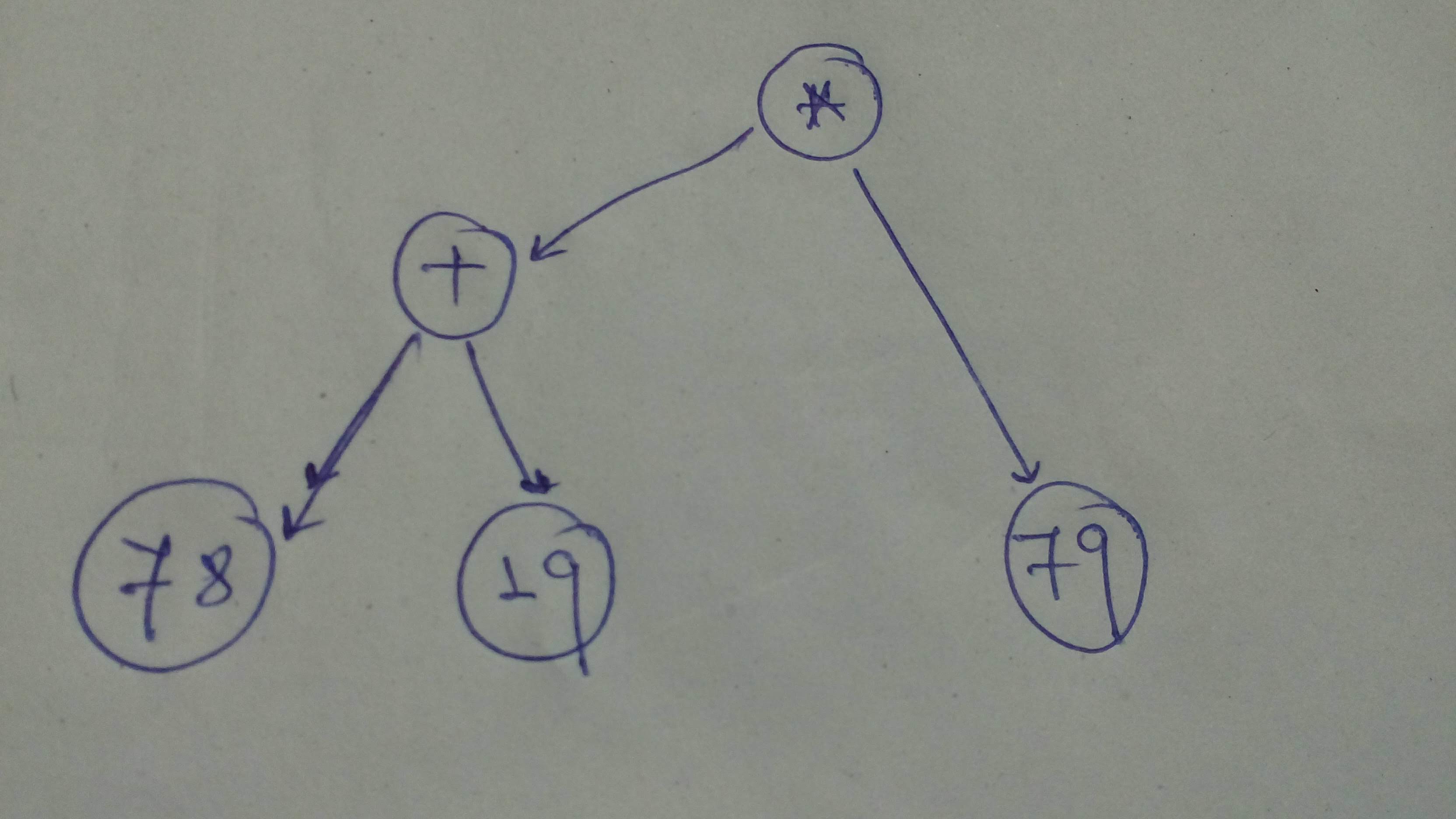"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "FyVz0GNqgreZ",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 51
+ },
+ "outputId": "7500a357-f1fe-4894-c1eb-ea6a7f1ab4e3"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the graph\n",
+ "comp_graph_1 = tf.multiply(tf.add(78, 19), 79)\n",
+ "\n",
+ "# Alternatively\n",
+ "comp_graph_1_alt = (tf.constant(78) + tf.constant(19)) * tf.constant(79)\n",
+ "\n",
+ "# Let's execute using session\n",
+ "sess = tf.Session()\n",
+ "print ('Comp Graph 1 : ', sess.run(comp_graph_1))\n",
+ "print ('Comp Graph 1 Alt: ', sess.run(comp_graph_1_alt))\n",
+ "sess.close()"
+ ],
+ "execution_count": 5,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Comp Graph 1 : 7663\n",
+ "Comp Graph 1 Alt: 7663\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "SVMMtuFYhaQB",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's define a sligtly more involved graph!\n",
+ "\n",
+ "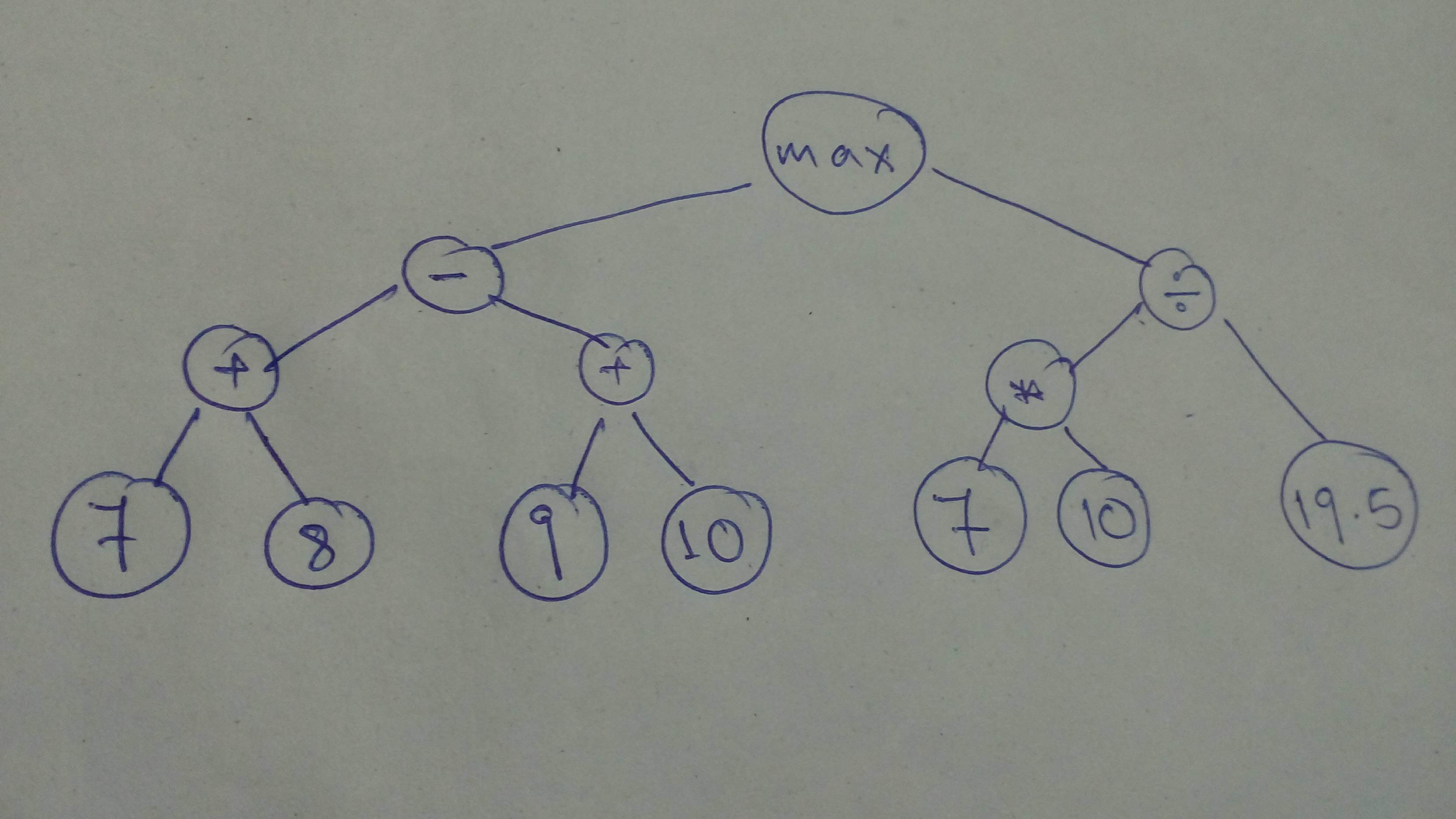"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "4856BTvRhiBb",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "1faf1c5b-9c96-4ea0-9011-b75f5b75e42a"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let build the graph\n",
+ "# We need to cast cause the tensors operated on should be of the same type\n",
+ "comp_graph_part_1 = tf.cast(tf.subtract(tf.add(7, 8), tf.add(9, 10)), \n",
+ " dtype=tf.float32)\n",
+ "comp_graph_part_2 = tf.divide(tf.cast(tf.multiply(7, 10), dtype=tf.float32), tf.constant(19.5))\n",
+ "comp_graph_complete = tf.maximum(comp_graph_part_1, comp_graph_part_2)\n",
+ "\n",
+ "# Let's execute\n",
+ "sess = tf.Session()\n",
+ "part1_res, part2_res, total_res = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n",
+ "print ('Complete Result: ', total_res)\n",
+ "print ('Part 1 Result: ', part1_res)\n",
+ "print ('Part 2 Result: ', part2_res)\n",
+ "sess.close()"
+ ],
+ "execution_count": 6,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: 3.5897436\n",
+ "Part 1 Result: -4.0\n",
+ "Part 2 Result: 3.5897436\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "B-_ZDtEbj4N0",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Cool! Let's go! Build another graph and execute it with sessions.
\n",
+ "\n",
+ "But this time, it's all you!\n",
+ "\n",
+ "Build this graph and execute it with `session`!\n",
+ "\n",
+ "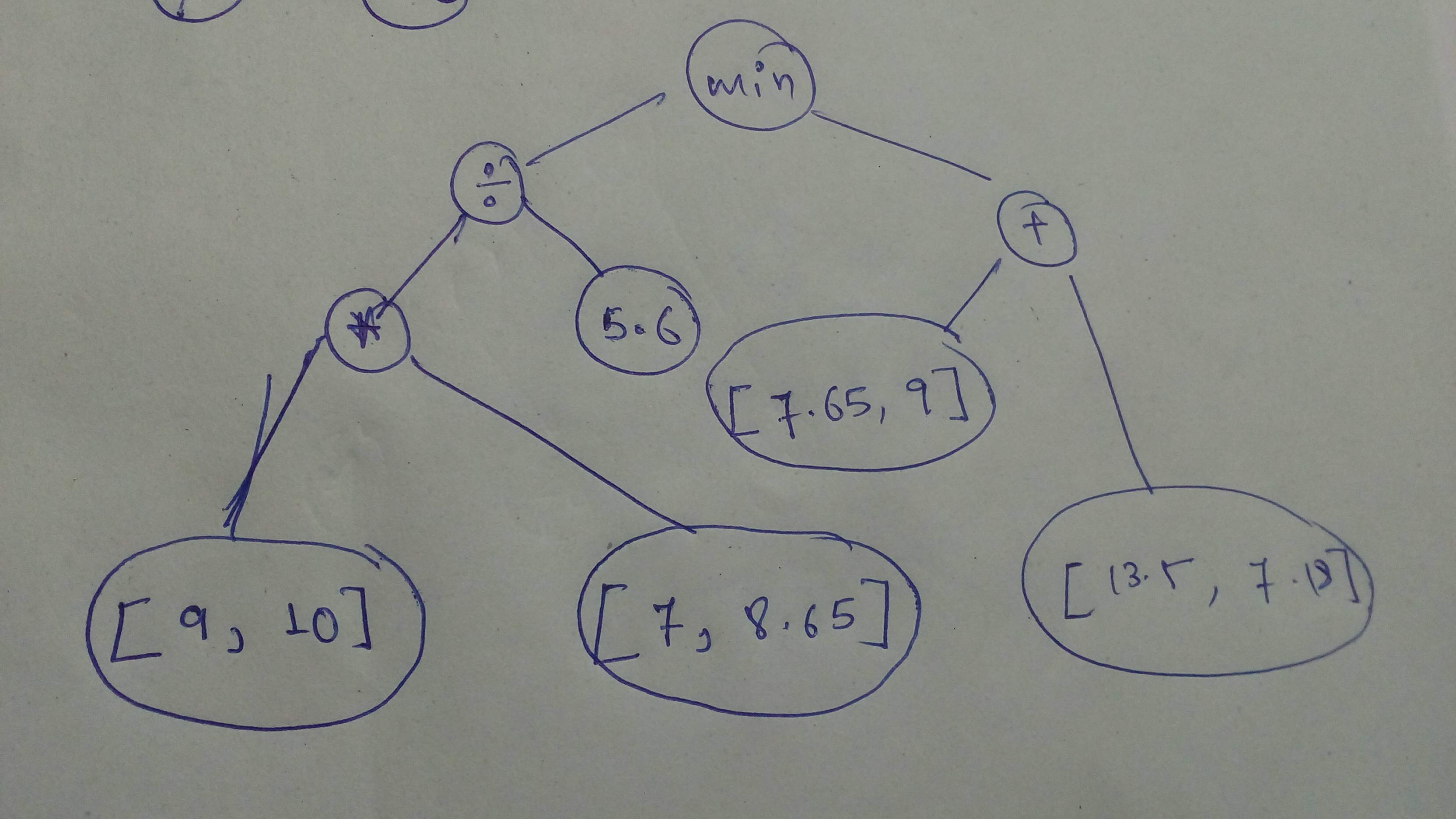\n",
+ "\n",
+ "_Remember that `tensors` operated on should be of the same type!_
\n",
+ "_Search up errors and other help you need on Google_"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "-uHNe1BolJY0",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 34
+ },
+ "outputId": "c0200506-8746-42cd-dd00-7260420395a0"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "comp_graph_3 = tf.constant([9 , 10], dtype = tf.float32 )\n",
+ "comp_graph_4 = tf.constant([7 , 8.65], dtype = tf.float32 )\n",
+ "comp_graph_5 = tf.constant(5.6 , dtype = tf.float32 )\n",
+ "comp_graph_6 = tf.constant([7.65 , 9], dtype = tf.float32 )\n",
+ "comp_graph_7 = tf.constant([11.5 , 7.18], dtype = tf.float32 )\n",
+ "comp_graph_8 = comp_graph_3 * comp_graph_4\n",
+ "comp_graph_9 = comp_graph_8 / comp_graph_5\n",
+ "comp_graph_10 = tf.add(comp_graph_6 , comp_graph_7)\n",
+ "comp_graph_total_1 = tf.minimum(comp_graph_9 , comp_graph_10)\n",
+ "\n",
+ "sess = tf.Session()\n",
+ "print(\"computational graph total :\" , sess.run(comp_graph_total_1))\n",
+ "sess.close()\n",
+ "\n",
+ "\n",
+ "\n",
+ "\n",
+ "# Execute \n",
+ "# YOUR CODE HERE"
+ ],
+ "execution_count": 7,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "computational graph total : [11.25 15.446429]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "qmap38WelREN",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's do another!
\n",
+ "It's fun! Isn't it?!\n",
+ "\n",
+ "Build and execute this one!\n",
+ "\n",
+ "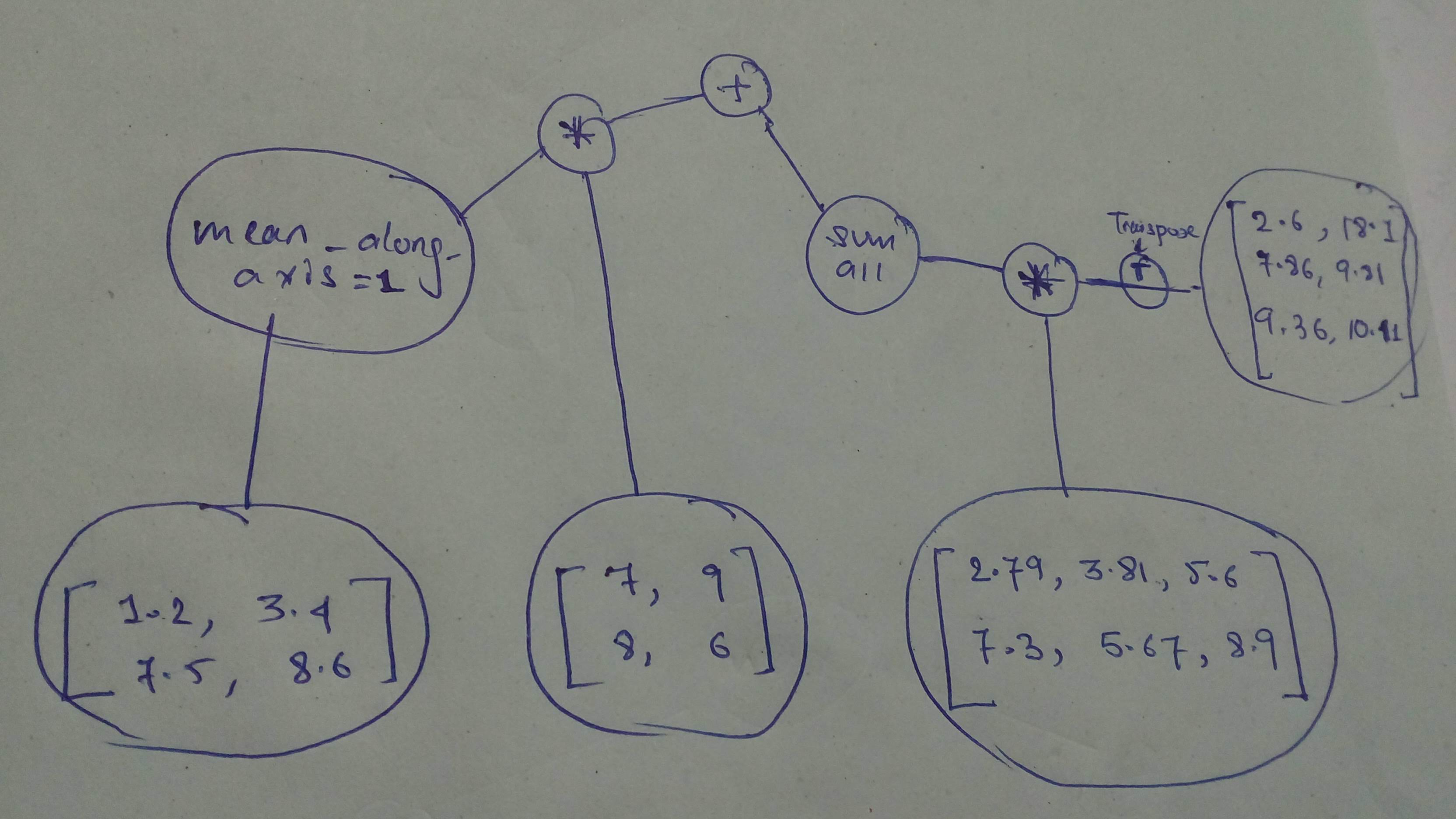"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "0ZhYwAlLmEvB",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1492
+ },
+ "outputId": "69817b68-b3aa-4bf5-a8d8-f301d45fc939"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "n1 = tf.constant([[1.2 , 3.4],\n",
+ " [7.5 , 8.6]] , dtype = tf.float32)\n",
+ "n2 = tf.constant([[7.0 , 9.0],\n",
+ " [8.0 , 6.0]] , dtype = tf.float32)\n",
+ "n3 = tf.constant([[2.79 , 3.81 , 5.6],\n",
+ " [7.3 , 5.57 , 8.9]] , dtype = tf.float32)\n",
+ "n4 = tf.constant([[7.6 , 18.1],\n",
+ " [7.86 , 9.81],\n",
+ " [9.36 , 10.11]] , dtype = tf.float32)\n",
+ "n4t = tf.transpose(n4)\n",
+ "n5 = tf.multiply(n3 , n4t)\n",
+ "\n",
+ "n6 = tf.reduce_sum(n5)\n",
+ "n7 = tf.reduce_mean(n7 , 1)\n",
+ "\n",
+ "n8 = tf.multiply(n3 , n2)\n",
+ "n9 = tf.add(n6 , n8)\n",
+ "sess = tf.Session()\n",
+ "print(\"n9:\" , sess.run(n9))\n",
+ "sess.close()\n",
+ "\n",
+ "\n",
+ "\n",
+ "\n",
+ "# Execute \n",
+ "# YOUR CODE HERE"
+ ],
+ "execution_count": 20,
+ "outputs": [
+ {
+ "output_type": "error",
+ "ename": "ValueError",
+ "evalue": "ignored",
+ "traceback": [
+ "\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
+ "\u001b[0;31mInvalidArgumentError\u001b[0m Traceback (most recent call last)",
+ "\u001b[0;32m/usr/local/lib/python3.6/dist-packages/tensorflow/python/framework/ops.py\u001b[0m in \u001b[0;36m_create_c_op\u001b[0;34m(graph, node_def, inputs, control_inputs)\u001b[0m\n\u001b[1;32m 1658\u001b[0m \u001b[0;32mtry\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 1659\u001b[0;31m \u001b[0mc_op\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mc_api\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mTF_FinishOperation\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mop_desc\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 1660\u001b[0m \u001b[0;32mexcept\u001b[0m \u001b[0merrors\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mInvalidArgumentError\u001b[0m \u001b[0;32mas\u001b[0m \u001b[0me\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
+ "\u001b[0;31mInvalidArgumentError\u001b[0m: Invalid reduction dimension 1 for input with 1 dimensions. for 'Mean_2' (op: 'Mean') with input shapes: [2], [] and with computed input tensors: input[1] = <1>.",
+ "\nDuring handling of the above exception, another exception occurred:\n",
+ "\u001b[0;31mValueError\u001b[0m Traceback (most recent call last)",
+ "\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m()\u001b[0m\n\u001b[1;32m 12\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 13\u001b[0m \u001b[0mn6\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mtf\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mreduce_sum\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mn5\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m---> 14\u001b[0;31m \u001b[0mn7\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mtf\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mreduce_mean\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mn7\u001b[0m \u001b[0;34m,\u001b[0m \u001b[0;36m1\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 15\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 16\u001b[0m \u001b[0mn8\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mtf\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mmultiply\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mn3\u001b[0m \u001b[0;34m,\u001b[0m \u001b[0mn2\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
+ "\u001b[0;32m/usr/local/lib/python3.6/dist-packages/tensorflow/python/ops/math_ops.py\u001b[0m in \u001b[0;36mreduce_mean_v1\u001b[0;34m(input_tensor, axis, keepdims, name, reduction_indices, keep_dims)\u001b[0m\n\u001b[1;32m 1532\u001b[0m keepdims = deprecation.deprecated_argument_lookup(\"keepdims\", keepdims,\n\u001b[1;32m 1533\u001b[0m \"keep_dims\", keep_dims)\n\u001b[0;32m-> 1534\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mreduce_mean\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0minput_tensor\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0maxis\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mkeepdims\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mname\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 1535\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1536\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
+ "\u001b[0;32m/usr/local/lib/python3.6/dist-packages/tensorflow/python/util/dispatch.py\u001b[0m in \u001b[0;36mwrapper\u001b[0;34m(*args, **kwargs)\u001b[0m\n\u001b[1;32m 178\u001b[0m \u001b[0;34m\"\"\"Call target, and fall back on dispatchers if there is a TypeError.\"\"\"\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 179\u001b[0m \u001b[0;32mtry\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 180\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mtarget\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m**\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 181\u001b[0m \u001b[0;32mexcept\u001b[0m \u001b[0;34m(\u001b[0m\u001b[0mTypeError\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mValueError\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 182\u001b[0m \u001b[0;31m# Note: convert_to_eager_tensor currently raises a ValueError, not a\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
+ "\u001b[0;32m/usr/local/lib/python3.6/dist-packages/tensorflow/python/ops/math_ops.py\u001b[0m in \u001b[0;36mreduce_mean\u001b[0;34m(input_tensor, axis, keepdims, name)\u001b[0m\n\u001b[1;32m 1590\u001b[0m gen_math_ops.mean(\n\u001b[1;32m 1591\u001b[0m \u001b[0minput_tensor\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0m_ReductionDims\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0minput_tensor\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0maxis\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mkeepdims\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 1592\u001b[0;31m name=name))\n\u001b[0m\u001b[1;32m 1593\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1594\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
+ "\u001b[0;32m/usr/local/lib/python3.6/dist-packages/tensorflow/python/ops/gen_math_ops.py\u001b[0m in \u001b[0;36mmean\u001b[0;34m(input, axis, keep_dims, name)\u001b[0m\n\u001b[1;32m 5569\u001b[0m _, _, _op = _op_def_lib._apply_op_helper(\n\u001b[1;32m 5570\u001b[0m \u001b[0;34m\"Mean\"\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0minput\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0minput\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mreduction_indices\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0maxis\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mkeep_dims\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mkeep_dims\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 5571\u001b[0;31m name=name)\n\u001b[0m\u001b[1;32m 5572\u001b[0m \u001b[0m_result\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0m_op\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0moutputs\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m]\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 5573\u001b[0m \u001b[0m_inputs_flat\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0m_op\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0minputs\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
+ "\u001b[0;32m/usr/local/lib/python3.6/dist-packages/tensorflow/python/framework/op_def_library.py\u001b[0m in \u001b[0;36m_apply_op_helper\u001b[0;34m(self, op_type_name, name, **keywords)\u001b[0m\n\u001b[1;32m 786\u001b[0m op = g.create_op(op_type_name, inputs, output_types, name=scope,\n\u001b[1;32m 787\u001b[0m \u001b[0minput_types\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0minput_types\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mattrs\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mattr_protos\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m--> 788\u001b[0;31m op_def=op_def)\n\u001b[0m\u001b[1;32m 789\u001b[0m \u001b[0;32mreturn\u001b[0m \u001b[0moutput_structure\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mop_def\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mis_stateful\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mop\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 790\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n",
+ "\u001b[0;32m/usr/local/lib/python3.6/dist-packages/tensorflow/python/util/deprecation.py\u001b[0m in \u001b[0;36mnew_func\u001b[0;34m(*args, **kwargs)\u001b[0m\n\u001b[1;32m 505\u001b[0m \u001b[0;34m'in a future version'\u001b[0m \u001b[0;32mif\u001b[0m \u001b[0mdate\u001b[0m \u001b[0;32mis\u001b[0m \u001b[0;32mNone\u001b[0m \u001b[0;32melse\u001b[0m \u001b[0;34m(\u001b[0m\u001b[0;34m'after %s'\u001b[0m \u001b[0;34m%\u001b[0m \u001b[0mdate\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 506\u001b[0m instructions)\n\u001b[0;32m--> 507\u001b[0;31m \u001b[0;32mreturn\u001b[0m \u001b[0mfunc\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m*\u001b[0m\u001b[0margs\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;34m**\u001b[0m\u001b[0mkwargs\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 508\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 509\u001b[0m doc = _add_deprecated_arg_notice_to_docstring(\n",
+ "\u001b[0;32m/usr/local/lib/python3.6/dist-packages/tensorflow/python/framework/ops.py\u001b[0m in \u001b[0;36mcreate_op\u001b[0;34m(***failed resolving arguments***)\u001b[0m\n\u001b[1;32m 3298\u001b[0m \u001b[0minput_types\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0minput_types\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 3299\u001b[0m \u001b[0moriginal_op\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_default_original_op\u001b[0m\u001b[0;34m,\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 3300\u001b[0;31m op_def=op_def)\n\u001b[0m\u001b[1;32m 3301\u001b[0m \u001b[0mself\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0m_create_op_helper\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mret\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mcompute_device\u001b[0m\u001b[0;34m=\u001b[0m\u001b[0mcompute_device\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 3302\u001b[0m \u001b[0;32mreturn\u001b[0m \u001b[0mret\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
+ "\u001b[0;32m/usr/local/lib/python3.6/dist-packages/tensorflow/python/framework/ops.py\u001b[0m in \u001b[0;36m__init__\u001b[0;34m(self, node_def, g, inputs, output_types, control_inputs, input_types, original_op, op_def)\u001b[0m\n\u001b[1;32m 1821\u001b[0m op_def, inputs, node_def.attr)\n\u001b[1;32m 1822\u001b[0m self._c_op = _create_c_op(self._graph, node_def, grouped_inputs,\n\u001b[0;32m-> 1823\u001b[0;31m control_input_ops)\n\u001b[0m\u001b[1;32m 1824\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1825\u001b[0m \u001b[0;31m# Initialize self._outputs.\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
+ "\u001b[0;32m/usr/local/lib/python3.6/dist-packages/tensorflow/python/framework/ops.py\u001b[0m in \u001b[0;36m_create_c_op\u001b[0;34m(graph, node_def, inputs, control_inputs)\u001b[0m\n\u001b[1;32m 1660\u001b[0m \u001b[0;32mexcept\u001b[0m \u001b[0merrors\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mInvalidArgumentError\u001b[0m \u001b[0;32mas\u001b[0m \u001b[0me\u001b[0m\u001b[0;34m:\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1661\u001b[0m \u001b[0;31m# Convert to ValueError for backwards compatibility.\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m-> 1662\u001b[0;31m \u001b[0;32mraise\u001b[0m \u001b[0mValueError\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mstr\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0me\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 1663\u001b[0m \u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 1664\u001b[0m \u001b[0;32mreturn\u001b[0m \u001b[0mc_op\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n",
+ "\u001b[0;31mValueError\u001b[0m: Invalid reduction dimension 1 for input with 1 dimensions. for 'Mean_2' (op: 'Mean') with input shapes: [2], [] and with computed input tensors: input[1] = <1>."
+ ]
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "BnB0b6qCmGmg",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "And a final one, before we move on to the next part!\n",
+ "\n",
+ "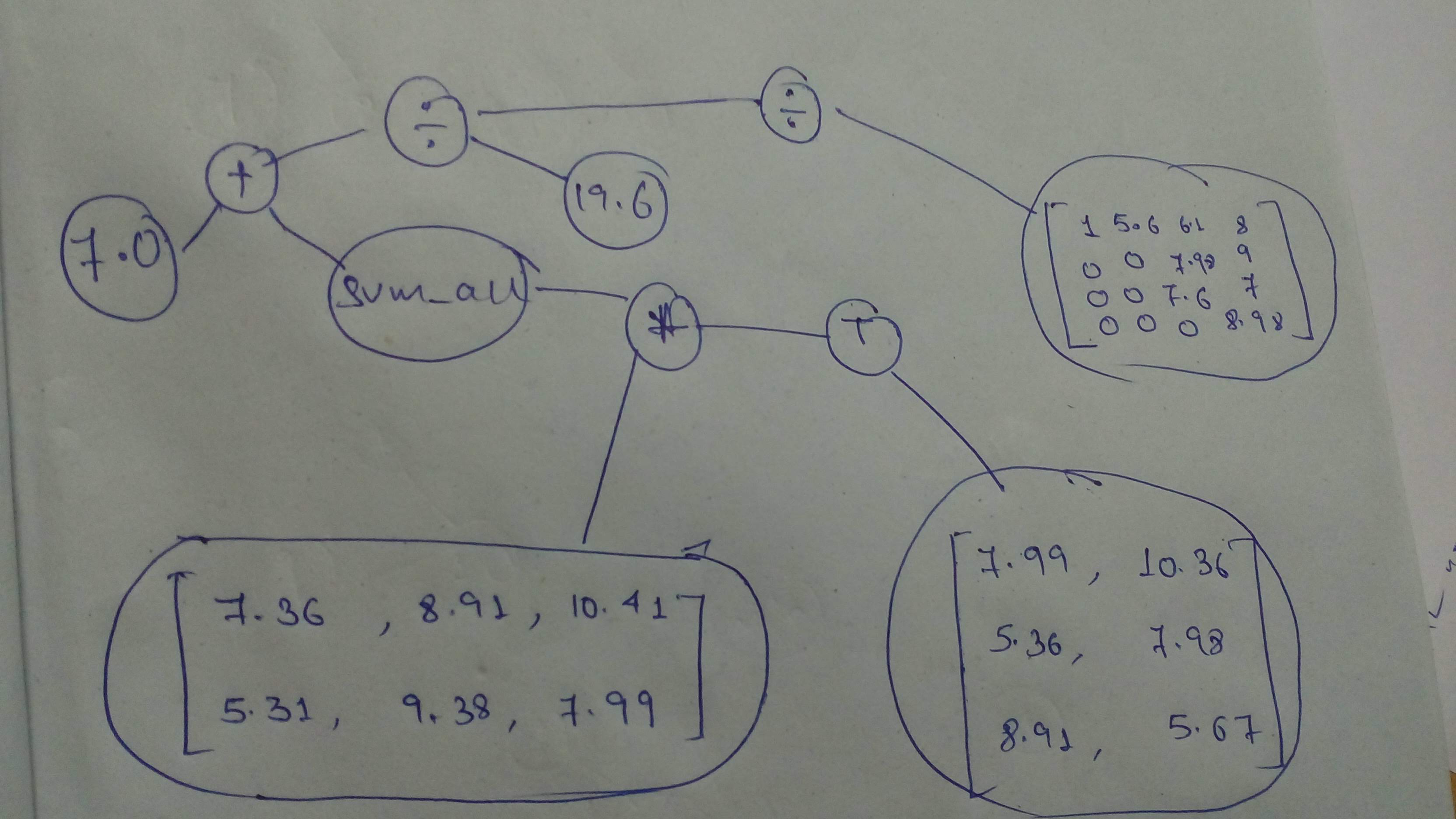"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "GQWyCvsQmMcL",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 85
+ },
+ "outputId": "4ec228e7-c52a-4372-9823-3272c95e1242"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "t1 = tf.constant([[7.36 , 8.91 , 10.41],\n",
+ " [5.31 , 9.18 , 7.99]], dtype = tf.float32)\n",
+ "t2 = tf.constant([[7.99 , 10.36],\n",
+ " [5.36 , 7.98],\n",
+ " [8.91 , 5.67]], dtype = tf.float32)\n",
+ "t3 = tf.constant([[1 , 5.6 , 6.1 , 8],\n",
+ " [0 , 0 , 7.98 , 9],\n",
+ " [0 , 0 , 7.6 , 7],\n",
+ " [0 , 0 , 0 , 8.98]], dtype = tf.float32)\n",
+ "t_single_1 = tf.constant(7.0 ,dtype = tf.float32)\n",
+ "t_single_2 = tf.constant(19.6 , dtype = tf.float32)\n",
+ "\n",
+ "t2t = tf.transpose(t2)\n",
+ "t4 = tf.multiply(t1 , t2t)\n",
+ "t5 = tf.reduce_sum(t4)\n",
+ "t6 = tf.add(t5 , t_single_1)\n",
+ "t7 = t6 / t_single_2\n",
+ "t8 = t3 / t7\n",
+ "sess = tf.Session()\n",
+ "print(\"final result :\",sess.run(t8))\n",
+ "sess.close()\n",
+ "\n",
+ "\n",
+ "# Execute \n",
+ "# YOUR CODE HERE"
+ ],
+ "execution_count": 17,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "final result : [[0.0515941 0.288927 0.31472403 0.41275284]\n",
+ " [0. 0. 0.41172096 0.46434695]\n",
+ " [0. 0. 0.3921152 0.36115873]\n",
+ " [0. 0. 0. 0.46331504]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "12NC7XTPsJw7",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# Linear Regression\n",
+ "\n",
+ "Okay, now we will create a dummy dataset and perform linear regression on this dataset!\n",
+ "\n",
+ "\n",
+ "To get you in the habit of looking up for the documentation, I am not providing what some of the following functions does, Google them up!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "hW31RZkjtNwI",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Create the dataset\n",
+ "X = np.linspace(-30.0, 300.0, 300)\n",
+ "Y = 2 * np.linspace(-30.0, 250.0, 300) + np.random.randn(*X.shape)\n",
+ "\n",
+ "# Normalize the dataset\n",
+ "X = X / np.max(X)\n",
+ "Y = Y / np.max(Y)\n",
+ "\n",
+ "# Divide it into train and test\n",
+ "train_X = X[:250]\n",
+ "train_Y = Y[:250]\n",
+ "\n",
+ "test_X = X[250:]\n",
+ "test_Y = Y[250:]"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "LQKy6U33y4lt",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the hyperparameters\n",
+ "learning_rate = 0.00001\n",
+ "n_epochs = 60\n",
+ "interval = 20"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "1h1-D8K1uT48",
+ "colab_type": "code",
+ "outputId": "3afd1637-e58c-4673-ee5d-ebb91d0ec8b1",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 347
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# let's viz the first 10 datapoints of the dataset\n",
+ "plt.plot(train_X[:10], train_Y[:10], 'g')\n",
+ "plt.show()"
+ ],
+ "execution_count": 23,
+ "outputs": [
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAfIAAAFKCAYAAADmCN3IAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3XlAlAX+x/H3cMkhIBiYJZaaSqV4\noFKaB5RHdpdY7KpRppmmpmYSmUepUKkppplprlumG7WVmWuWImmSF4bmL49yzYNCSBQBhQGe3x9t\nbKz3OPAwzOf1T/HM8zzz+fpkn5nnYeaxGIZhICIiIg7JxewAIiIiYjsVuYiIiANTkYuIiDgwFbmI\niIgDU5GLiIg4MBW5iIiIA3MzO4AtsrNP2X2fAQHe5OYW2n2/1Zlmdg7OODM459yauWYLCvI953K9\nI/8PNzdXsyNUOc3sHJxxZnDOuTWzc1KRi4iIODAVuYiIiANTkYuIiDgwFbmIiIgDU5GLiIg4MBW5\niIiIA1ORi4iIODAVuYiIiANTkYuIiDgwFbmIiIgDU5GLiIjYSXFpMWmZ37Dsh/coKSupkud0yJum\niIiIVAeGYXDg5I+sP7yO9YfXsfHoBgqs+QA0Dwylbb12lZ5BRS4iInIZTpzJZcPR1PLyPnzqUPlj\nN9RpSreQKLpf16tKShxU5CIiIhdUUlbC9qxtrD+8lvWH17Hj2HbKjDIA/GvV4Z4m9xMZcjtdQyIJ\n8W1Y5flU5CIiIv/j4Ml/k/Kf4t549GtOFecB4Gpxpf3VEXQLiaJbSBStg9ri6mLurVRtKnKr1Upc\nXByZmZm4urqSkJBASEhIhXVWrFjBkiVLcHFxoW/fvkRHR1NYWEhcXBw5OTl4eXmRmJhIUFAQe/bs\nYdKkSQA0b96cyZMnX/FgIiIilyqv6CQbj24of9d9MO/f5Y9d79eIh5pGE9nwDjpdcxt+tfxNTHo2\nm4p85cqV+Pn5MWPGDDZu3MiMGTOYNWtW+eOFhYXMnTuXDz/8EHd3d/r06UP37t355JNPCAkJISkp\niW3btpGUlMTLL7/M1KlTiY+PJywsjDFjxpCamkrXrl3tNqSIiMiflZaVsuPY9vLr3NuztlJqlALg\n6+FH70b30C0kiq4hkTTyb2xy2guzqcjT0tK4//77AejYsSPx8fEVHs/IyKBly5b4+voC0LZtW9LT\n0zl48CC33norAO3atWPChAkUFxdz9OhRwsLCAIiMjCQtLU1FLiIidnX41KHy4v76yHpOFp0AwMXi\nQtvgdv85XX47beuF4+biOFeebUqak5NDYGAgAC4uLlgsFoqLi/Hw8DjrcYDAwECys7Np1qwZqamp\n9OzZky1btpCZmUlubi5+fn7l69atW5fs7OwLPn9AgDdubva/JhEU5Gv3fVZ3mtk5OOPM4Jxza+b/\nOlV0ivUH17PmpzWsObCGfb/tK3/sOv/rePjmvvRo0oOoRlEEeAVUVVy7u2iRJycnk5ycXGFZRkZG\nhZ8Nw7jgPv54vE+fPuzdu5eYmBg6dOhQoewvdV8AubmFF13ncgUF+ZKdfcru+63ONLNzcMaZwTnn\ndvaZS8tK2ZWTUf6ue+uvm7GWWQHwca9Nr+t70zUkisiQKBr5N8FisQBQkg/Z+dX/z+18L1guWuTR\n0dFER0dXWBYXF0d2djahoaFYrVYMwyh/Nw4QHBxMTk5O+c/Hjh2jdevWeHh4lP8iW0FBAWvXriUw\nMJATJ06Ur5uVlUVwcPDlTSciIk7pSN4RPvphBesPr+XrI+s5fuY4ABYstA5uU366vF29Dri7upuc\ntnLYdGq9U6dOrF69ms6dO5OSkkJERESFx1u1asX48ePJy8vD1dWV9PR04uPjSU1NZceOHTzzzDOs\nWLGCzp074+7uTuPGjdm2bRvt2rVjzZo19O/f3y7DiYhIzVJgLeDbzG9Yf3gdKYfXsi93b/lj1/hc\ny19vHEC3kCg6N+hKoGddE5NWHZuKvHfv3mzatImYmBg8PDxITEwEYMGCBbRv3542bdowZswYBg4c\niMViYdiwYfj6+hIREcHSpUvp27cv/v7+zJw5E4D4+HgmTJhAWVkZrVq1omPHjvabUEREHJZhGHyf\ns5OUw+tIPbyOzb+kUVxWDIC3mze9m/amY3AXIhvewQ11mpafLncmFuNSLkpXM5VxDcjZry05C83s\nPJxx7po282+nf2PkuqdY8/Pq8mVhQa3p1iCKbg2jaH91BA2uvqpGzXwhNl8jFxERqWppmd8w5MuB\n/FKQSadrOtPvpkfp0iCSIO8gs6NVOypyERGpNkrLSpmVPp3XtiZgwcL4WybxdJtncLHortvnoyIX\nEZFqIavgV4Z+NYgNR1O5tnYD5nd/h4j6t5gdq9pTkYuIiOnWHfqKp9cOJud0Dr0a3cXsyLkEeJ79\nXSNyNhW5iIiYxlpqJXHLFObseB0PFw+m3fYqA1s+6ZS/fW4rFbmIiJji8KlDPLnmcbZlbaGRf2Pe\n7vE3woJamx3L4ajIRUSkyn1+4DOeSRnGyaITPNg0mte6vo6vh9/FN5SzqMhFRKTKnCk5w+S08Sza\ntQAvNy9mRc4lJrSfTqVfARW5iIhUiZ9O7GfQmsf4PmcnoYE3sqDH3wgNvNHsWA5PH8wTEZFKl7x3\nObd/0IXvc3bS/6ZYVj+UohK3E70jFxGRSlNgLSB+w1iW7XmP2u6+vNX9HR5o2sfsWDWKilxERCrF\n//22m8FrYtmXu5dWQW14q8c7NPZvYnasGken1kVExK4Mw2DJ7nfo9WEk+3L38mTYUFY+uEYlXkn0\njlxEROwmr+gkY9aP5NOf/kmdWnVY0ONv9GrU2+xYNZqKXERE7GJH1nYGf/kYP+cdpMPVt/BW93e4\n1reB2bFqPJ1aFxGRK2IYBm9+9wZ3f9yDQ3k/Myr8WT65f5VKvIroHbmIiNjst9O/MWLdEL78+QuC\nvIKZd8fbdA2JNDuWU1GRi4iITdIyv2HIlwP5pSCTLg0imXvHAup51zM7ltNRkYuIyGUpLStlVvp0\nXtuagAUL8RETGNF2NC4WXa01g4pcREQuWVbBrwz9ahAbjqZybe0GzO/+DhH1bzE7llNTkYuIyCVZ\nd+grnl47mJzTOfS6vjezo+YR4BlodiynpyIXEZELspZaSdwyhTk7XsfdxZ0pnRIZFPaU7lhWTajI\nRUTkvA6fOsSTax5nW9YWrvdrxNs9/kar4DZmx5I/UZGLiMg5fX7gM55JGcbJohM8cMNDTO82G18P\nP7Njyf9QkYuISAVnSs4wOW08i3YtwMvNi5nd5vDXGwfoVHo1pSIXEZFyP53Yz6A1j/F9zk6aB4Ty\nds8lum94NacP/YmICADJe5dzR3JXvs/ZSb8bH+WLPutV4g5A78hFRJxcgbWA+A1jWbbnPXzcazO/\n+yIebBptdiy5RCpyEREn9n+/7Wbwmlj25e4lLKg1C3os1n3DHYxOrYuIOCHDMFiy+x16fRjJvty9\nDGo5hM8f/FIl7oD0jlxExMnkFZ1kzPqRfPrTP6lTqw5v9VjMnY3uMjuW2EhFLiLiRHZkbWfwl4/x\nc95B2l8dwVvd36GBb4jZseQK6NS6iIiTWL5nKXd/3INDeT8zsu0YPrlvlUq8BtA7chERJ/Dx/g8Z\nuW4oAZ4BzO/+Dt1CosyOJHaiIhcRqeHWHPwXw9YOpraHLx/c8wlhQa3NjiR2pFPrIiI12MajXzPw\niwF4uHjw/l0fqsRrIBW5iEgNtT1rK/0+fxjDMFjcaykR9W8xO5JUAptOrVutVuLi4sjMzMTV1ZWE\nhARCQir+wsSKFStYsmQJLi4u9O3bl+joaAoLC4mLiyMnJwcvLy8SExMJCgqif//+FBYW4u3tDcC4\nceNo0aLFlU8nIuKkdud8T8zKhygqPcPCnn8nsuHtZkeSSmJTka9cuRI/Pz9mzJjBxo0bmTFjBrNm\nzSp/vLCwkLlz5/Lhhx/i7u5Onz596N69O5988gkhISEkJSWxbds2kpKSePnllwFISEigWbNm9plK\nRMSJHTjxI30/u58TRSeYEzWfuxrfY3YkqUQ2nVpPS0uje/fuAHTs2JH09PQKj2dkZNCyZUt8fX3x\n9PSkbdu2pKenc/DgQcLCwgBo164d27dvv8L4IiLyZ0dOHabPivvIPn2MhM7TeTj0L2ZHkkpm0zvy\nnJwcAgMDAXBxccFisVBcXIyHh8dZjwMEBgaSnZ1Ns2bNSE1NpWfPnmzZsoXMzMzydZKSksjNzaVJ\nkybEx8fj6el53ucPCPDGzc3VlugXFBTka/d9Vnea2Tk448zgfHNn5WfxyKoHOJJ/mGlR04jrPMbs\nSFXC2Y7z/7pokScnJ5OcnFxhWUZGRoWfDcO44D7+eLxPnz7s3buXmJgYOnToUF72AwYMoHnz5jRs\n2JCJEyeydOlSBg4ceN795eYWXiz2ZQsK8iU7+5Td91udaWbn4Iwzg/PNfeJMLn0+v4d9v+1jeJtR\nPBH6tFPM70zH+XwvWC5a5NHR0URHV7ydXVxcHNnZ2YSGhmK1WjEMo/zdOEBwcDA5OTnlPx87dozW\nrVvj4eHB5MmTASgoKGDt2rUA5afpAaKioli1atVljCYi4tzyrfnEfN6HnVk7ib15IONvmWR2JKlC\nNl0j79SpE6tXrwYgJSWFiIiICo+3atWKXbt2kZeXR0FBAenp6bRr147U1NTyX4pbsWIFnTt3xjAM\nYmNjycvLA2Dz5s00bdr0SmYSEXEaZ0rO8OiqmN8/ahbWj8QuM7BYLGbHkipk0zXy3r17s2nTJmJi\nYvDw8CAxMRGABQsW0L59e9q0acOYMWMYOHAgFouFYcOG4evrS0REBEuXLqVv3774+/szc+ZMLBYL\nffv2JTY2Fi8vL+rVq8fw4cPtOqSISE1kLbUyeE0sG46mcmeju1l832JyfzttdiypYhbjYhe4q6HK\nuB7iTNdZ/qCZnYMzzgw1f+4yo4yhXw3in/uT6dIgkqV3fUCDq6+q0TOfS00/zn92vmvk+mY3EREH\nYxgG474ewz/3J9P+6giW3Pk+tVxrmR1LTKIiFxFxIIZh8FLaBJbsXkSLq8J4/65kfNx9zI4lJlKR\ni4g4kFnbpzP3u9ncUKcp/7j7Y/xr1TE7kphMRS4i4iAW7pxPwpaXCfFtyIf3riDIO8jsSFINqMhF\nRBzA8j1Lid/4HMHe9Ui+91OuqX2t2ZGkmlCRi4hUc5/99CnPpAwjoFYAyfd8SmP/JmZHkmpERS4i\nUo2tO/QlQ758HC83b5bf/U9urHuT2ZGkmlGRi4hUU99mbuKx1f1wtbjyXu9/0KZeuNmRpBqy6Zvd\nRESkcmUc28FfPo/GWmbl73cuo9O1nc2OJNWUilxEpJrZe3wPD698gMKSAt7q/g53XNfT7EhSjanI\nRUSqkYMn/02fFfdy/MxxXu/2Bvfd8KDZkaSa0zVyEZFq4pf8TPp8dh9Zhb/ycqcE/nrTALMjiQNQ\nkYuIVAO/nf6N6M/u41DeQca2f54nWw0zO5I4CBW5iIjJ8opO8vDKB9iXu5chrZ7m2XZxZkcSB6Ii\nFxExUaG1kL+u6svO7O/od+OjTO44FYvFYnYscSAqchERkxSVFvHY6r+y+Zc07r/hQV7rOkslLpdN\nRS4iYoKSshKe+vIJUg6vpft1PXnj9gW4uriaHUsckIpcRKSKlRlljEp5mpUHPqXTNZ1Z2PPveLh6\nmB1LHJSKXESkChmGwfiN4/jH3vdpGxzOu72X4+XmZXYscWAqchGRKpS45WUW7nqLGwNvYtndH1Hb\nw9fsSOLgVOQiIlXkjR2zeX37dBr5N+aDez4hwDPQ7EhSA6jIRUSqwJLd7/BS2otc43MtH967gno+\nV5sdSWoIFbmISCX7aN8HPJc6iqu8ruLDe1cQ4tvQ7EhSg6jIRUQq0b/+/TlPr30SXw8//nHPJ9wQ\n0NTsSFLDqMhFRCrJ10fWM+iLR6nlWov37/qQlleFmR1JaiAVuYhIJdj662YGrIoBYMmdy+hQP8Lk\nRFJT6X7kIiJ29n3OLv7yeTRFpWd4p9d7dA2JNDuS1GAqchERO/oxdz99P7ufvKKTvHH7W9zZ6C6z\nI0kNpyIXEbGTw6cO0WfFveSczubVLq8T3fwRsyOJE9A1chERO8gqzKLPinvJLDjKi7e+RGyLgWZH\nEiehIhcRuUK5Z47Td8X9/PvkAZ5p+yzD2zxjdiRxIipyEZErkF98ipiVD/HD8d0MbDmY5yNeNDuS\nOBkVuYiIjU6XnGbAv2JIP7adh5v/ham3vYrFYjE7ljgZFbmIiA2spVYGffEoG49+zV2N7+X1yDdw\nseh/qVL19F+diMhlMAyDjUe/5oFP72LNz6vpFhLF/O6LcHPRh4DEHPovT0TkEhiGwfrD65ix7RW2\n/PotAHc2upt5d7xNLddaJqcTZ6YiFxG5AMMw+OrnL5ix7RXSj20HoNf1vRkVPpY29cJNTidiY5Fb\nrVbi4uLIzMzE1dWVhIQEQkJCKqxz8uRJRo8ejY+PD0lJSRfcbs+ePUyaNAmA5s2bM3ny5CubSkTk\nCpUZZaz+9ypmbn+VndnfAXBX43sZHT6WlkGtTE4n8l82XSNfuXIlfn5+LFu2jCFDhjBjxoyz1pk4\ncSLh4eGXtN3UqVOJj49n+fLl5Ofnk5qaakssEZErVmaUseLHj4n8RydiV/+FXdkZ3H/Dg6x/OI3F\nvd5TiUu1Y1ORp6Wl0b17dwA6duxIenr6WetMmTLlrCI/13bFxcUcPXqUsLDfb+8XGRlJWlqaLbFE\nRGxWWlbKR/s+oMvyCJ5Y8yh7c3+gT7OH2fDIFhb0+Bs31b3Z7Igi52TTqfWcnBwCAwMBcHFxwWKx\nUFxcjIeHR/k6tWvXvqTtcnJy8PPzK1+nbt26ZGdnX/D5AwK8cXNztSX6BQUF+dp9n9WdZnYOzjgz\nXNrcJWUlLN25lGkbp7Hvt324Wlx5rPVjPH/b8zSt27QKUtqXMx5rZ5z5zy5a5MnJySQnJ1dYlpGR\nUeFnwzBsevJzbXcp+8rNLbTp+S4kKMiX7OxTdt9vdaaZnYMzzgwXn7u4tJjkvcuZlT6dn/MO4u7i\nTv+bYhneZhTX+zeCMhzuz80Zj7UzzXy+FywXLfLo6Giio6MrLIuLiyM7O5vQ0FCsViuGYVR4N34+\nwcHBZ20XFBTEiRMnytfJysoiODj4ovsSEbFFUWkRy354j6T0mRzJP4yHiwePtXiC4W1G0cA35OI7\nEKlmbLpG3qlTJ1avXg1ASkoKERERNm/n7u5O48aN2bZtGwBr1qyhc+fOtsQSETmv0yWnWbhzPh3e\na8VzX48i53Q2g8OeYmu/nbzSZaZKXByWTdfIe/fuzaZNm4iJicHDw4PExEQAFixYQPv27QkLCyM2\nNpa8vDyysrLo378/Q4cOPe928fHxTJgwgbKyMlq1akXHjh3tN6GIOLUCawF/372Yud/N5lhhFt5u\n3gxtPYKnWg+nnnc9s+OJXDGLYesFbhNVxvUQZ7rO8gfN7ByccWYATz94df3rzM+YQ87pHHzcazOw\nxWCGtH6aq7yuMjtepXDGY+1MM9t8jVxExJHkFZ1k4a63WLBrHsdPH8fPw5/R7Z7jybChBHgGmh1P\nxO5U5CJSI5w4k8uCnW+yYOeb5BWfJMAzgHEdXuCJlk/iX6uO2fFEKo2KXEQc2m+nf+OtjLks3PUW\n+dZT1PWsy/hbJjG22yiK8nRvcKn5VOQi4pCOFR7jze/msPj7hRSWFBDkFcyz7eN49ObH8XH3wa+W\nL9k4x7VTcW4qchFxKL8W/MLcHbP5+/8t5nTJaa72qU98xIv0uykWb3dvs+OJVDkVuYg4hKOnjjBn\nx+ss/eHvFJUWcW3tBgxvO4q/hPbH083T7HgiplGRi0i1dijvZ2anz2T5nvewlllp6Hc9I9uO5uHm\nf8HD9eLfKClS06nIRaRaOnDyJ5K2z+SDfcsoKSuhkX9jRoWP5aGmfXF3dTc7nki1oSIXkWrlx9z9\nvL79NT7a/wFlRhlN6zRjVLux3H/DQ7i56H9ZIv9LfytEpFrYc/wHXt/2Kp/8+E8MDG4MvIlR4WO5\np8n9uLrY/7bFIjWFilxETDdp03jmfZcEQIurwhgd/hy9G9+Ni8Wm+zqJOBUVuYiY6suDq5n3XRKN\n/ZswudM0elzXC4tFX+QicqlU5CJimpNFJxiTOhJ3F3cW91rKjXVvMjuSiMPReSsRMc3Eb17g14Jf\nGN3uOZW4iI1U5CJiipRDa3l/z7u0uCqMEW1Gmx1HxGGpyEWkyuUXn2LM+hG4ubgxO2qePhcucgVU\n5CJS5SanTeBI/mFGtB1Ny6vCzI4j4tBU5CJSpTYcSWXJ7kWEBt7IqPCxZscRcXgqchGpMvnWfEat\nH46LxYXZkfOo5VrL7EgiDk9FLiJVZtq3kzmUd5BhrUfSpl642XFEagQVuYhUiW8zN7Fw11s0rdOM\nse2fNzuOSI2hIheRSldoLeSZlGFYsDAraq7uHy5iRypyEal0r2yZyoGTP/Fkq2G0vzrC7DgiNYqK\nXEQq1bZft/DWzrk08m9MXIfxZscRqXFU5CJSac6UnGHkuqGUGWXMipyLt7u32ZFEahwVuYhUmulb\nE9l/Yh8DWw7m1ms6mR1HpEZSkYtIpfjuWDpzv5tNQ7/reeGWSWbHEamxVOQiYnfFpcWMXDeMUqOU\n17vNobZ7bbMjidRYKnIRsbvXt7/GD8d3M+Cmx+ncoKvZcURqNBW5iNjVrpydzE6fwbW1GzCx40tm\nxxGp8VTkImI31lIrI9cNpaSshBndkvD18DM7kkiNpyIXEbuZs+N1vs/ZSUxoP6Ia3mF2HBGnoCIX\nEbvYc/wHZmx7hat96vNSp2lmxxFxGipyEbliJWUljFz3FNYyK9O7zsK/Vh2zI4k4DRW5iFyxNzPe\nYMexdPo0e5ge199pdhwRp6IiF5Ersj93H69umUqQVzBTbks0O46I01GRi4jNSstKGbluKEWlRbzS\nZSaBnnXNjiTidNxs2chqtRIXF0dmZiaurq4kJCQQEhJSYZ2TJ08yevRofHx8SEpKuuB2/fv3p7Cw\nEG/v32+oMG7cOFq0aHGFo4lIZXt715tsy9rCfU0e5O4m95odR8Qp2fSOfOXKlfj5+bFs2TKGDBnC\njBkzzlpn4sSJhIeHX/J2CQkJvPvuu7z77rsqcREHcODkTyRsfpm6nnVJ6DLd7DgiTsumIk9LS6N7\n9+4AdOzYkfT09LPWmTJlyllFfinbiUj1V2aUMSrlaU6XnCah83Su8rrK7EgiTsumU+s5OTkEBgYC\n4OLigsViobi4GA8Pj/J1atc++yYJ59sOICkpidzcXJo0aUJ8fDyenp7nff6AAG/c3FxtiX5BQUG+\ndt9ndaeZnYO9Z567ZS5pmd/wQOgDPHHro1gsFrvu3150rJ2DM878Zxct8uTkZJKTkyssy8jIqPCz\nYRg2Pfkf2w0YMIDmzZvTsGFDJk6cyNKlSxk4cOB5t8vNLbTp+S4kKMiX7OxTdt9vdaaZnYO9Z/45\n7yDPfTmOOrXq8NItr5KTk2+3fduTjrVzcKaZz/eC5aJFHh0dTXR0dIVlcXFxZGdnExoaitVqxTCM\nCu/Gzyc4OPic2/1xuh0gKiqKVatWXXRfIlL1DMNg9PoRFJYU8GrXt6jnXc/sSCJOz6Zr5J06dWL1\n6tUApKSkEBERYfN2hmEQGxtLXl4eAJs3b6Zp06a2xBKRSvbu//2NDUfW0/26nkQ3e8TsOCKCjdfI\ne/fuzaZNm4iJicHDw4PExN+/BGLBggW0b9+esLCw8nLOysqif//+DB069JzbWSwW+vbtS2xsLF5e\nXtSrV4/hw4fbdUgRuXJHTx1h0qbx+Hn4M73r7Gp7XVzE2VgMWy9wm6gyroc403WWP2hm52CPmQ3D\nIObzh1h36CtmRc7lLzf2t1O6yqNj7RycaebzXSPXN7uJyEX9Y+/7rDv0Fd1CoogJ7Wd2HBH5ExW5\niFzQrwW/8OI3z+PjXpuZ3ebolLpINWPTNXIRcQ6GYTA29RlOFp3g1S6v08A35OIbiUiV0jtyETmv\nj/Z/wBcH/8Vt13ZhwM2PmR1HRM5BRS4i53Ss8BgvbHgObzdvZnabg4tF/7sQqY50al1Ezinu6zHk\nFuUy7bZXud6/kdlxROQ89BJbRM6y4sePWXngUyLq38rjLQebHUdELkBFLiIV5JzOIW7DGDxdPZkd\nOVen1EWqOf0NFZEKXtgw9vcyj3iRxnVuMDuOiFyEilxEyq06sJKPf/yI8HrteTJsqNlxROQSqMhF\nBIDcM8cZm/oMtVxrMTtyHq4urmZHEpFLoCIXEQBe/OZ5sk8fY2z752kW2NzsOCJyiVTkIsKXB1fz\nwd5ltApqw9DWI8yOIyKXQUUu4uTyik7ybOozuLu4MztqHm4u+noJEUeiIhdxchM3vcAvBZmMCh/L\nTXVvNjuOiFwmFbmIE0s5tJalP/ydm+u2ZGTbMWbHEREbqMhFnFR+8SnGrB+Bm4sbSVHzcHd1NzuS\niNhARS7ipF5Km8CR/MOMaDOKlkGtzI4jIjZSkYs4oY1Hv+ZvuxcRGngjo9o9Z3YcEbkCKnIRJ1Ng\nLWBUytO4WFyYHTmPWq61zI4kIldARS7iZKZ9O5mf8w4ytPUI2tQLNzuOiFwhFbmIE/n2lzQW7nqL\nG+o05bn28WbHERE7UJGLOIlCayHPrPv9RiizIufh6eZpciIRsQcVuYiTeHXrNA6c/InBrYbSoX6E\n2XFExE5U5CJOYHvWVuZnvMH1fo14vsOLZscRETtSkYvUcGdKzjBy3VDKjDJmRc7F293b7EgiYkcq\ncpEa7qXUl9iXu5fHWwyi47W3mR1HROxMRS5Sg2Uc28Gr37xKQ9/rGH/rZLPjiEglUJGL1FDFpcWM\nWDeUUqOUmZFzqO1e2+xIIlIJVOQiNdSs7dP54fhuBrcdTJcG3cyOIyKVxM3sACLVlWEYrPl5NYfy\nDuLt5oO3uzfe7j54u3nj4+5T/u9//NPLzQuLxWJ2bAC+z9nFrPTpXONzLa/1eI2iPLMTiUhlUZGL\nnEPO6RzGrB/Bv/698pK3sWD5U7l74+Ne+79F7+79nxcAtX9/zO3PLwpqlz9+1jJ3b7zdfKjlWuuS\nXyRYS62MXDeUkrISZkYm4VfwHC4yAAAYhklEQVTLj2xO2fpHISLVnIpc5H+sOfgvnkl5mpzT2XS6\npjOPtxzE6ZLTFFoLKbAWUFhSQKG1sPyfFZcVUmDNp9BayImiIxRY8ykpK7niTK4W1wovErzdfP5z\nVsD7v2cL/rPsaP4RduVk8EjoX4lq2N0OfyIiUp2pyEX+I9+az8RvXuDd/1uMh4sHkztO48lWQ3Gx\nXNmvkhSXFlNoLaCwpLD8BUCBtaB8WYH1Pz+XFP6+7BJeMOSczqHAmk+ZUXbO57zapz4vdZx2RblF\nxDGoyEWAbb9uYdjawfz75AFuqtuCeXe8zU11b7bLvj1cPfBw9aAOAXbZ3x8Mw6CotOi/hW/9z9mA\nkkKa1LmBOp72fT4RqZ5U5OLUrKVWZmx/hVnbp2MYBk+3eYZxHV5wiHt0WywWPN088XTzJNCzrtlx\nRMQkKnJxWvtz9zH0q0FkZO8gxLchb9z+Frde08nsWCIil8Wmi39Wq5UxY8YQExNDv379OHz48Fnr\nnDx5koEDBzJixIgKy7ds2cKtt95KSkpK+bI9e/bwyCOP8MgjjzBx4kRbIolcMsMwWLTrLW7/4DYy\nsnfwcPO/sP7hTSpxEXFINhX5ypUr8fPzY9myZQwZMoQZM2actc7EiRMJDw+vsOzQoUMsXryYtm3b\nVlg+depU4uPjWb58Ofn5+aSmptoSS+SiMk9l8vDKB3h+w1i83b1Z1PNd5tw+H18PP7OjiYjYxKYi\nT0tLo3v33z/W0rFjR9LT089aZ8qUKWcVeVBQEG+88Qa+vr7ly4qLizl69ChhYWEAREZGkpaWZkss\nkQta8ePHtJjXgvWH13F7w+6kPvwt9zS5z+xYIiJXxKZr5Dk5OQQGBgLg4uKCxWKhuLgYDw+P8nVq\n1z77e529vLzOWpabm4uf33/fDdWtW5fs7OwLPn9AgDdubq62RL+goCDfi69UwzjDzCfOnGD4v4bz\n3s738Hb35s273uTJ8CerzbewVQVnOM7n4oxza2bnc9EiT05OJjk5ucKyjIyMCj8bhmG3QJeyr9zc\nQrs93x+CgnzJznaub79yhpm/ObqBp9c+ydH8I7QNDmdZ3/cJKKtPTk6+2dGqjDMc53Nxxrk1c812\nvhcsFy3y6OhooqOjKyyLi4sjOzub0NBQrFYrhmFUeDd+OQIDAzlx4kT5z1lZWQQHB9u0L5E/nCk5\nQ8Lml5mf8QYuFhfGtn+eUeFjqV83wGn+0ouIc7DpGnmnTp1YvXo1ACkpKURERNgcwN3dncaNG7Nt\n2zYA1qxZQ+fOnW3en8j3Obvo+WE33syYQyP/xnz+4JeMbf88bi76tKWI1Dw2/Z+td+/ebNq0iZiY\nGDw8PEhMTARgwYIFtG/fnrCwMGJjY8nLyyMrK4v+/fszdOhQioqKWLRoEQcOHGD37t28++67vPPO\nO8THxzNhwgTKyspo1aoVHTt2tOuQ4hxKy0qZlzGHxM0vYy2z8liLJ5hw68v4uPuYHU1EpNJYDHte\n4K4ilXFq1Jmus/yhJs18KO9nnl77JN/+solg73rMjpzL7df1OGu9mjTzpXLGmcE559bMNZvN18hF\nqjPDMPjH3veJ3/Ac+dZT3N34Pl7rOou6XvrKUhFxDipycVi/nf6NZ1NH8vmBFdR292VO1Hz6No9x\nqo+ViYioyMUhffXzF4xcN4zs08e49ZpOzImaT0O/68yOJSJS5VTk4lAKrAVM2jSeJbsX4eHiwcRb\npzCk1TBcXez/BUEiIo5ARS4OY3vWVoZ9NZgDJ3/ixsCbmXfH29x8VQuzY4mImEpFLtWetdTKzO2v\nMmv7dMqMMoa2HkFch/F4unmaHU1ExHQqcqnWfszdz7C1g9hxLJ0GtUOYc/t8Ol2rLwwSEfmDilyq\nJcMwWLx7IZM3jed0yWmimz1CQufX8Kvlb3Y0EZFqRUUu1U5Wwa+MTBnKukNfEVArgDlR87n3hgfM\njiUiUi2pyKVa+eynT3l2/Qhyi3KJDLmd2VHzuNqnvtmxRESqLRW5VAt5RSeJ3/gcH+xdhpebF4ld\nZvDYzU/oy11ERC5CRS6m23R0I0+vfZIj+YdpE9yWube/zQ0BTc2OJSLiEFTkYpqi0iISNr/Mm9/N\nwcXiwph24xgd/hzuru5mRxMRcRgqcjHF7pzvGfrVIH44vptG/o2Ze/sC2l3dwexYIiIOR0UuVaq0\nrJT5GXNJ2PwSxWXFPHrzQCZ1nKJ7houI2EhFLlXm8KlDDF87hE2ZGwnyCmZW5Bt0v76X2bFERBya\nilyqxMqfVjAyZSinivPo3egepnebzVVeV5kdS0TE4anIpVJZS6289O0E3sqYi7ebN7Mj5/FI6F/1\nsTIRETtRkUulOXrqCIPWxLItawtN6zRjUa93CQ280exYIiI1iopcKsW6Q18x9KsnOH7mOA827cP0\nbknUdq9tdiwRkRpHRS52VVpWymvbEnh922u4u7jzSpeZxN48UKfSRUQqiYpc7OZY4TGe+uoJNhxZ\nT0Pf61jYcwmtg9uaHUtEpEZTkYtdfJu5iUFrYskq/JVe1/cmKepN6ngGmB1LRKTGU5HLFSkzypj7\nXRLTvp0MwIRbX2ZY6xE6lS4iUkVU5GKzE2dyGb5uCF8c/BdX+9RnQffF3HJNR7NjiYg4FRW52GRH\n1nYGrYnl0Kmf6dygG/PvWESQd5DZsUREnI6L2QHEsRiGwaJdC7jn454cPnWIZ9vF8cHdH6vERURM\nonfkcsnyi08xZv0IPv7xI+p61mXeHQuJbHi72bFERJyailwuyQ+//R8Dv+jPjyf20/7qCN7u8Teu\nqX2t2bFERJyeTq3LRS3fs5ReH0Xy44n9PNVqOJ/ct0olLiJSTegduZzX6ZLTxG8Yy9If/o6fhz9v\n9lpE78Z3mx1LRET+REUu53TgxI8M/OJRdv+2i5ZXtWJhzyU08m9sdiwREfkfOrUuZ/nsp0+5I7kr\nu3/bxYCbHufzB79UiYuIVFN6Ry7likuLeSntRRbsfBNvN2/m3fE2fZo9bHYsERG5ABW5AHDk1GEG\nrYlle9ZWmgU0Z1HPd2keGGp2LBERuQgVubD25zUM/WoQuUW5PNS0L691m6V7h4uIOAgVuRMrLSsl\nYfNLvL59Oh4uHrzWdRYDbnpMNzwREXEgNhW51WolLi6OzMxMXF1dSUhIICQkpMI6J0+eZPTo0fj4\n+JCUlFS+fMuWLYwcOZJp06YRGRkJQP/+/SksLMTb2xuAcePG0aJFC1tnkkuQVZjFw6sGk3IwhYZ+\n1/NOz78TFtTa7FgiInKZbCrylStX4ufnx4wZM9i4cSMzZsxg1qxZFdaZOHEi4eHh7Nmzp3zZoUOH\nWLx4MW3btj1rnwkJCTRr1syWOHKZNh3dyOAvH+NYYRZ3NrqbpKh5+NeqY3YsERGxgU0fP0tLS6N7\n9+4AdOzYkfT09LPWmTJlCuHh4RWWBQUF8cYbb+Dr62vL08oVKjPKmL19Bg+uuJvjZ35jRo8Z/K3X\nUpW4iIgDs+kdeU5ODoGBgQC4uLhgsVgoLi7Gw8OjfJ3atc/+ZSkvL6/z7jMpKYnc3FyaNGlCfHw8\nnp6e5103IMAbNzdXW6JfUFBQzX2Bcfz0cR77eACf7/+ca32v5R99/kGnhp3MjmWKmnycz8cZZwbn\nnFszO5+LFnlycjLJyckVlmVkZFT42TCMKwoxYMAAmjdvTsOGDZk4cSJLly5l4MCB510/N7fwip7v\nXIKCfMnOPmX3/VYH6VnbGLQmlsOnDtEtJIp5dyzkKq+rAGrszOdTk4/z+TjjzOCcc2vmmu18L1gu\nWuTR0dFER0dXWBYXF0d2djahoaFYrVYMw6jwbvxy/XGaHiAqKopVq1bZvC/5L8MweOf7BUz4Jp6S\nshKeax/PqPCxuLrY/2yGiIiYw6Zr5J06dWL16tUApKSkEBERYXMAwzCIjY0lLy8PgM2bN9O0aVOb\n9ye/O1Wcx+A1j/H8hrH41/Lng3s+4dn2cSpxEZEaxqZr5L1792bTpk3ExMTg4eFBYmIiAAsWLKB9\n+/aEhYWVl3NWVhb9+/dn6NChFBUVsWjRIg4cOMDu3bt59913eeedd+jbty+xsbF4eXlRr149hg8f\nbtchnc3unO8Z+EV/Dpz8iYj6t7Kg+2Lq177G7FgiIlIJLMaVXuA2QWVcD6kp11mW/fAe474ezZnS\nMwxrPZL4iAm4u7qfc92aMvPl0MzOwxnn1sw1m83XyMUxFFoLeX7Dsyzb8x7+teqwoMff6NWot9mx\nRESkkqnIa4CfTuzn8dUD+OH4bloFtWFhzyVc53e92bFERKQK6H7kDm7Fjx/TPbkbPxzfTezNA/ns\ngS9U4iIiTkTvyB1UcWkxkza9wMJdb+Ht5sObdyzkoWZ9zY4lIiJVTEXugLb9uoUXNj7HjmPphAbe\nyKKe79I0QN9TLyLijFTkDmTf8b1M2/wSq/79GQB9m8fwSpeZ+Lj7mJxMRETMoiJ3AEdPHeG1rQks\n37uUMqOMdvU6MOHWl7jlmo5mRxMREZOpyKux42d+Iyn9dRbteoui0iJCA28kPmIiPa+/E4vFYnY8\nERGpBlTk1VCBtYC3d77JnB2zOFWcx7W1GzCuwwtEN3tEX7EqIiIVqMirEWuplfd+WMKMba9wrDCL\nQM9AXuo0jdibn8DT7fy3dRUREeelIq8GyowyVvz4MQlbXubfJw/g7ebD6HbPMaz1CHw9/MyOJyIi\n1ZiK3ESGYbD+8Dqmbp7MzuzvcHNx4/EWgxjdbhzB3sFmxxMREQegIjdJetY2pnw7iY1HvwbgwabR\nxHUYz/X+jUxOJiIijkRFXsV+zN3PtM0vsfLApwDc3rA78bdMpOVVYSYnExERR6QiryKZ+UeZvjWR\nZXveo9QoJbxee168ZTIdr73N7GgiIuLAVOSVLPfM8fLPgp8pPUOzgObER0zkzkZ36bPgIiJyxVTk\nlaTQWsjCXfOZs2MWJ4tOcG3tBjzXPp7o5o/g5qI/dhERsQ81ip1ZS628v+ddpm9NJKvwVwJqBTCp\n41QebzFInwUXERG7U5HbSZlRxmc/fULC5pc5cPInvN28GRX+LMNaj8Svlr/Z8UREpIZSkdtB6uEU\npnw7iYzsHbi5uBF780DGtBtHPZ+rzY4mIiI1nIr8Cnx3LJ0p307m6yMpADxww0OMixhPY/8mJicT\nERFnoSK3wU8n9pOweQorfvoYgMiQ2xl/yyRaBrUyOZmIiDgbFfll+LXgF17bmsj7P/ydUqOUtsHh\njL91Mrdd28XsaCIi4qRU5JfgxJlc5uyYxcJd8zldcpob6jQlPmIidzW+R58FFxERU6nIL+B0yWkW\n7nqLOekzOVF0gvo+1zDtttd4OPQv+iy4iIhUC2qjcygpK2HZnvd4bWsCvxb8Qp1adZhw68sMbDkY\nLzcvs+OJiIiUU5H/iWEYrDzwKdM2v8RPJ37Ey82LkW3H8HSbkfjXqmN2PBERkbOoyP9j3b/X8ezq\nsew4lo6rxZVHbx7ImHbPcbVPfbOjiYiInJfTF3mBtYAnvhjA2kNfAnBfkwd5PmI8jevcYHIyERGR\ni3P6Is85nc2mzI3c0fgOxrV9kVbBbcyOJCIicsmcvsiv87uen544Sv16AWRnnzI7joiIyGVxMTtA\ndaCPkomIiKNSkYuIiDgwFbmIiIgDU5GLiIg4MBW5iIiIA1ORi4iIODCbfl3barUSFxdHZmYmrq6u\nJCQkEBISUmGdkydPMnr0aHx8fEhKSgKgpKSEF154gUOHDlFaWspzzz1Hu3bt2LNnD5MmTQKgefPm\nTJ48+cqmEhERcRI2vSNfuXIlfn5+LFu2jCFDhjBjxoyz1pk4cSLh4eEVln366ad4eXmxbNkypk6d\nSmJiIgBTp04lPj6e5cuXk5+fT2pqqi2xREREnI5NRZ6Wlkb37t0B6NixI+np6WetM2XKlLOK/N57\n7+X5558HIDAwkBMnTlBcXMzRo0cJCwsDIDIykrS0NFtiiYiIOB2bTq3n5OQQGBgIgIuLCxaLheLi\nYjw8PMrXqV279lnbubu7l//7kiVLuPvuu8nNzcXPz698ed26dcnOzr7g8wcEeOPm5mpL9AsKCvK1\n+z6rO83sHJxxZnDOuTWz87lokScnJ5OcnFxhWUZGRoWfDcO4rCddunQpu3fvZv78+Rw/fvyy95Wb\nW3hZz3cpgoJ8ne4rWjWzc3DGmcE559bMNdv5XrBctMijo6OJjo6usCwuLo7s7GxCQ0OxWq0YhlHh\n3fiFJCcns27dOubNm4e7u3v5KfY/ZGVlERwcfEn7EhERcXY2nVrv1KkTq1evpnPnzqSkpBAREXFJ\n2x0+fJjly5fz3nvvUatWLeD30+2NGzdm27ZttGvXjjVr1tC/f/8L7qeyTqM44+kZzewcnHFmcM65\nNbPzsRiXe14cKC0tZfz48Rw8eBAPDw8SExOpX78+CxYsoH379oSFhREbG0teXh5ZWVk0bdqUoUOH\nkpaWxueff84111xTvq9FixZx6NAhJkyYQFlZGa1atSr/hTgRERG5MJuKXERERKoHfbObiIiIA1OR\ni4iIODAVuYiIiANTkYuIiDgwmz5+5khsvcHL+bZzhBu8XMrMK1asYMmSJbi4uNC3b1+io6MpLCwk\nLi6OnJwcvLy8SExMJCgoiP79+1NYWIi3tzcA48aNo0WLFmaMdl72nrkmH+esrCzi4+MpLi6mrKyM\n559/nhYtWhAVFcXVV1+Nq+vv35o4ffp06tWrZ8ZoF2TvuTdt2sTMmTNxdXWlS5cuDBs2zKTJzs/W\nmd988002bdoEQFlZGTk5OXzxxRcOcaztPbMjHGebGTXcP//5T2PSpEmGYRjGhg0bjJEjR561zsiR\nI425c+caw4cPv+h2/fr1MzIyMgzDMIzRo0cb69evr+wRLtvFZi4oKDB69Ohh5OXlGadPnzbuuusu\nIzc311i8eLHx6quvGoZhGFu3bjXGjx9vGMbvM+/du7dqh7hMlTFzTT3OiYmJxrJlywzDMIzt27cb\njz/+uGEYhhEZGWnk5+dX7RA2sPfcd955p5GZmWmUlpYaMTExxv79+6t2oEtg68z/u4+3337bMAzH\nONb2ntkRjrOtavypdVtv8HKu7RzlBi8XmzkjI4OWLVvi6+uLp6cnbdu2JT09nYMHD5bP1q5dO7Zv\n317l2W1lz5lr+nEOCAgo/zbFvLw8AgICqjz7lbDn3IcPH8bf35/69evj4uJC165da9Sx/kNJSQnL\nli2jX79+VZr7SthzZkc5zraq8afWbb3By7m2y8nJuewbvJjhYjP/+XH4/U502dnZNGvWjNTUVHr2\n7MmWLVvIzMwsXycpKYnc3FyaNGlCfHw8np6eVTvURdhzZltu5GMGW2eOjY2lT58+fPLJJ+Tn57Ns\n2bLydSZOnMjRo0cJDw9nzJgxWCyWqh3qEthz7uzs7LPWPXz4cNUOdAlsnfkPa9as4bbbbqvw97a6\nH2t7zuwox9lWNarIK+MGLxfaztZ92ZM9Zv7j8T59+rB3715iYmLo0KFD+X/4AwYMoHnz5jRs2JCJ\nEyeydOlSBg4caMcpLk9VzHw5+6oK9px54cKF3HnnnTz11FOkpKTwyiuv8MYbbzBixAg6d+6Mv78/\nw4YN44svvqBXr172HeQyVfbcjz/+uH0D24E9Z/7DRx99VOH3PKrbsa6KmWuyGlXk9rzBS3Bw8Fnb\nBQUFVbsbvNgyc3BwMDk5OeU/Hzt2jNatW+Ph4VH+H35BQQFr164FKD+9BRAVFcWqVasqc6SLquyZ\nq+ONfOw585dffskzzzwD/H7fhD/mv//++8vX7dKlC/v27TO9yCt77v9dt6Yda4DCwkJ+/fVXGjRo\nUP54dTvWlT1zdTzO9lTjr5H/cYMX4LJu8HKu7f58gxf4/dRN586dKyf4FbjYzK1atWLXrl3k5eVR\nUFBAeno67dq1IzU1lVmzZgG//zZo586dMQyj/HvzATZv3kzTpk2rdqBLYM+Za/pxvu6668rf7ezc\nuZPrrruOU6dOMXDgQIqLiwHYunVrtTzOYN+5GzRoQH5+PkeOHKGkpISUlBQ6depU5TNdjK0zA+zZ\ns4fGjRuXr+sox9qeMzvKcbZVjf+udVtv8NKhQ4dzbvfjjz9W+xu8XGzmNm3asHr1ahYtWoTFYqFf\nv37ce++9nDlzhhEjRnDixAn8/f2ZOXMmvr6+rFq1ioULF+Ll5UW9evWYOnUqXl5eZo9Zgb1nrsnH\n+dixY7zwwgucOXMGgBdeeIHQ0FCWLFnCJ598Qq1atbjpppt48cUXq911U7D/3Fu3bmX69OkA9OjR\nw9TLRudj68xA+Uev/nya2RGOtb1ndoTjbKsaX+QiIiI1WY0/tS4iIlKTqchFREQcmIpcRETEganI\nRUREHJiKXERExIGpyEVERByYilxERMSBqchFREQc2P8Dcme/9h+wcwoAAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jrsUps0nu8vj",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "** Question **
\n",
+ "Why did I created a session to plot the graph?
\n",
+ "[Ans]"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "P3-iuxE4sjAf",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the placeholders\n",
+ "\n",
+ "# Placeholders?\n",
+ "# The input to the model changes on iteration\n",
+ "# So we cannot have a constant in the input as we did before\n",
+ "# And thus we need placeholders which we can change on each \n",
+ "# iteration of the training\n",
+ "\n",
+ "x = tf.placeholder(tf.float32, name='x')\n",
+ "y = tf.placeholder(tf.float32, name='y')"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "8hPRkaoxvRyV",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 88
+ },
+ "outputId": "638a4b59-74b3-472c-fd39-f169a5459f34"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the linear regression model\n",
+ "\n",
+ "# tf.Variable?\n",
+ "# We define the model parameters as tf.Variables\n",
+ "# as they get updated throghout the training.\n",
+ "# And variables denotes something which changes overtime.\n",
+ "\n",
+ "W = tf.Variable(np.random.random_sample(), name='weight_1')\n",
+ "b = tf.Variable(np.random.random_sample(), name='bias_1')\n",
+ "\n",
+ "pred_y = (W*x) + b"
+ ],
+ "execution_count": 25,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.\n",
+ "Instructions for updating:\n",
+ "Colocations handled automatically by placer.\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "cSw1P8bkv96r",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the loss function\n",
+ "# We are going to use the mean squared loss\n",
+ "loss = tf.reduce_mean(tf.square(y - pred_y))"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "5G4uQqjsygNj",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 88
+ },
+ "outputId": "467f707a-cf84-4762-e50f-f9b83248fda6"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the optimizer\n",
+ "# And specify the which value (i.e. loss) it has to minimize\n",
+ "optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)"
+ ],
+ "execution_count": 27,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.\n",
+ "Instructions for updating:\n",
+ "Use tf.cast instead.\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "ttI7ZT-ozAm1",
+ "colab_type": "code",
+ "outputId": "6909cfaf-7ce3-4010-95f7-af88312bb007",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 432
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# So the graph is now built\n",
+ "# Now let's execute the graph using session\n",
+ "# i.e. lets train the model\n",
+ "\n",
+ "# What it is to train a model?\n",
+ "# To update the paramters in the graph (i.e. tf.Variables)\n",
+ "# So that the loss is minimized\n",
+ "\n",
+ "# Okay let's start!\n",
+ "with tf.Session() as sess:\n",
+ " # We need to initialize the variables in our graph\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ " \n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ " \n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ " \n",
+ " \n",
+ " print ('The final loss is: ', final_loss)\n",
+ " \n",
+ " # Plotting the final predictions against the true predictions\n",
+ " plt.plot(test_X, test_Y, 'g', label='True Function')\n",
+ " plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()"
+ ],
+ "execution_count": 28,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.052007735\n",
+ "Loss after epoch 20 is 0.05197699\n",
+ "Loss after epoch 40 is 0.05194628\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.004058556\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAe0AAAFKCAYAAAAwrQetAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3XlcVPX+x/HXGZgZxAFZBBfcEnfc\nU1zIHfcNzdTUrNzKrexaWliZP/clb3krM7Oy0qJriJj7gllXBc2dMhUFN1T2nYFZfn/QnfKmggoM\nM3yej0cPmTlzznw+DPHmbN+vYjabzQghhBCizFNZuwAhhBBCFI2EthBCCGEjJLSFEEIIGyGhLYQQ\nQtgICW0hhBDCRkhoCyGEEDbC0doF3E9CQoa1S8Dd3ZmUlGxrl1FipD/bZu/9gf33KP3ZvuLu0cvL\n5Z7LZE+7EI6ODtYuoURJf7bN3vsD++9R+rN9pdmjhLYQQghhIyS0hRBCCBshoS2EEELYCAltIYQQ\nwkZIaAshhBA2QkJbCCGEsBES2kIIIYSNKNODq5RF//rXP/n9999ITk4iNzeX6tV9cHWtxKJFy4tl\n+8OGDcTbuwoq1Z9/T33wwSePvN2ff/6Rdu06kp6exrp1a5g1a84jb1MIIUTpKlJonz9/nilTpvDc\nc88xZsyYO5YdOnSIlStX4uDgQOfOnZk6dSoAixYt4tSpUyiKQnBwMM2bNyc+Pp5Zs2ZhNBrx8vJi\n+fLlaDSa4u+qBE2f/goA27dv5dKlGKZNm1Hs77FixSqcnZ2LdZvffruB1q3b4ulZWQJbCCFsVKGh\nnZ2dzfz58+nQocNdly9YsIB169ZRpUoVxowZQ+/evUlOTiYuLo6QkBBiYmIIDg4mJCSEVatWMWrU\nKPr27cvKlSvZtGkTo0aNKvamrOH48WN8++3XZGdnM23aK8ycOY1t2/YB8Oabsxg6dDiNGjVm0aJ5\nZGRkYDQamTHjNerVq1+k7ffv3+Nv2ztx4heysjK5ciWO69ev8dJLM+nQIYCdO7exaVMIiqIwcuRo\n8vPz+fXXs7z66ku8/vpbzJv3JuvWfcXx48f4/PM1mM0KXl7evPHG2+zdu4vTp0+SmprClStxjBr1\nDAMGBJXY900IIUTRFRraGo2GtWvXsnbt2r8tu3r1KpUqVaJatWoAdOnShcOHD5OcnExgYCAAvr6+\npKWlkZmZSWRkJPPmzQOgW7dufPbZZ48U2u8cepOtMWEPvf7dDPQN4p2OCx5q3ZiYi3zzTeg9jx58\n9903tGvXkYEDg7h8+RLvv7+C99776FHK5fbtW6xYsYojRw6xZcv3tGjRki+++JT1678hLy+fhQvn\nsmTJSj799GNWrFhFWlqqZd0VKxbz5ZfrcXTUsXLlUvbs2YmiKMTEXOTjjz/j2rWrzJ0bLKEthCi3\nzGYz2YZsMvLSSdOnkZ6XRro+jfQ/HhvNRqYETASUUqmn0NB2dHTE0fHuL0tISMDDw8Py2MPDg6tX\nr5KSkoKfn98dzyckJJCTk2MJNE9PTxISEu773u7uzvcd09W5ggaVqni/Uc4VNH8brP1ug7e7uDjh\n7Pzna93cnGnSpDE+Pp4AKIpiWabVqnFzc+b336NJTk4mImI3AHp9zt+27eCg4o03XsHBoaBvd3d3\nVq1addftVayopUOHdnh5udCw4WPo9Tmkpd2mfv161KjhBcC6dWst261cWYeDQz6OjirUaiOOjg6W\nP7i6du3E0aNHadKkCW3bPk7Vqm64uKjJycm67+D1tsDW6y+MvfcH9t+j9Fc2rTi0gjf3v4neqL/v\n63yr1OIpv6dKpaZSuRDNbDYX6bn/VdisKbNavc2sVm8/dF338tfZxby8XO4621hGRi7Z2XmWZamp\n2ZjNiuWx2Wy2fJ2VlWNZPn36TJo2bX7X9wIwGk0sXvzPO85pJyRk3HV7WVl61OoKJCRkkJKSRV6e\ngbS0XHJz8+663cTETNLSsjAYTCQlZWEwGC3bT0pKJzfXQEZGLnl5JhISMsjOzsZoNJWJ2dYe1r0+\nP3th7/2B/fco/ZVN+6/s4bU9r1G5QmUCvDpRSVMJF00lKmkr4apxxfWPf72cvQlq3K9Ye7zfHzmP\nFNre3t4kJiZaHt+6dQtvb2/UavUdz9++fRsvLy+cnZ3Jzc3FycnJ8lp7pSgKubm5AJw//zsATZo0\n5eDBAzRt2pzLly8RGXmIkSPH3G8z993e3dSuXYcrV+LIzs7GwcGB2bNf4Z///BBFUWE0Gi2vc3V1\nRVEUbty4gVrtwsmTx2nevOUdrxFCiPLoesY1puydiEal4Zv+39PCu9V9X++gspFZvmrUqEFmZibX\nrl3DYDAQERFBQEAAAQEB7Nq1C4Do6Gi8vb3R6XR07NjR8vzu3bvp1KnTo3dQRgUFDWPSpGdZtGge\nDRs2BmDYsBFcv36VKVMmsHTpAlq2bP1I27ubChUqMH78i8yYMYXp019g4MAgFEWhVavWTJky/o5z\n2rNmvcnMmTOZNm0SBoOBHj16PXzDQghhB/KN+Uza8zzJucnMf2JJoYFd2hRzIcepz549y9KlS7l+\n/TqOjo5UqVKF7t27U6NGDXr27MnRo0dZsWIFAL169WL8+PEArFixgmPHjqEoCnPnzqVRo0bcvn2b\n2bNno9frqV69OosXL0atVt/zvcvCIRVbPbRTVNKfbbP3/sD+e5T+ypZ3Dr3JRydXMaTek3zc8zMU\npfDrpoq7x/sdHi80tK2pLHzQtvYD96CkP9tm7/2B/fco/ZUdOy9vZ+yOkfi61WPPsB/RaYp2AV1p\nhrYMYyqEEKLcu5Iex/T9L+Lk4MS63l8VObBLmwxjKoQQolzTG/VM3P0safpU3u/2EU08/QpfyUpk\nT1sIIUS5Nu/Qm5y4fZyRjUbzdOOi3dFjLRLaQgghyq3wi5v59MwaGns0YUmnd61dTqEktIUQQpRL\nl1IvMiNiGs6OFfm095c4q4t3oqaSIOe0H1B8/A3Gjh1Jw4aNAMjLy2P06Gfp0qXbA2/r++9DSE1N\npXPnrhw8eIDx41+46+v+O63m/W6P+69Lly6ycuWyv03n2aVLO5o1a2F57Onpybx5ix+45v8VEbGX\nbt0CuXDh9/v2IIQQZcmR+MNM3/cCmfkZrA78lPruDaxdUpFIaD+EWrVqW0IxPT2N558fTfv2HdBq\nnR5qe/XrN6R+/Yb3XP7faTWLEtr3otPpimVe7v/19dfr6dYtsNAehBCiLMjMz2TRkXmsO1Pw+3Bm\nm9k82WC4lasqOgntR+TqWglPz8okJSXx+edrcXRUk56eyv/93xKWLVvIjRvXMRgMTJjwIo8/3pZj\nx6JYtepdPDw88fSsTPXqPhw/fozQ0O9YsGDZfafVfP/91YSHb2bv3p0oiopOnbry9NNjuH37Fm+9\n9TpqtZp69Yr+12J8/A1eeOEN1qxZD8D48c+wYMFSPvvsEypX9uL333/j1q2bvP32Aho2bMSGDes5\ncGAfiqLixRence7cr1y8eJ7g4NcYNmyEpYd9+/YQErIBBwcHGjZszIwZr7Ju3Zq7TiMqhBCl5cer\nEcw88BJXMuKo79aAf3b7EP9q7axd1gOx6dCu+M6baLcW79Sc+oFBZL1T9Kk54+NvkJ6ehrd3FaBg\nTO/Zs+ewc+c2PD0r88Ybb5OamsrLL7/I+vXfsmbNB7z11nzq12/Aq6++RPXqPpZtZWdn3XdazYSE\n2xw4sI+PPloHwOTJ4+nWLZDQ0BB69OjF8OFP8/XXX3Dx4vlH/j7k5eWxcuUHhIVtYufObTg7O3Pg\nwD7WrPmCGzeu8/XXX/D662+xYcN6Fi1azvHjx/7oIZtPPvmQzz/fiLOzM7NmvWJZ9r/TiEpoCyFK\nQ7o+jXcOvcnXv63HQXHg5dYzmdlmNk6OD3d01JpsOrSt5cqVOKZNmwQUzDf+5pvzLNOXNmlScH/f\n2bOnOXXqBKdPnwRAr9eTn59PfHw89esX7A23bNkavf7PKd9iYy9Tq1YdtFontFonlixZecf7/vZb\nNNeuXWX69ILzxtnZWdy8eYPY2Mt061Ywf3mrVm04cuTQ32rOzMy01Azg61vvvpOVtGhRMN6ul1cV\nfv01mvPnf6dJk6aoVCpq1KjJ66+/ddf1rl69Qo0atSyzlLVq9Tjnz58DoHnzlkDBRDOZmZn3fG8h\nhCguu2N38OqPM7iZFU8Tz6as6v4Rzb1aWrush2bToZ31zoIH2isuLn89p/2/HB3Vln/Hjh1Hz559\n7liuUv15wf7/jiCrUjlgNpvu+b6Ojmo6dAhg1qw5dzy/YcN6FEX1xzbvvv7dzmnfvBl/x2ODwWD5\n+r/zef+3TgcHFSZT4SPeKsqdfRkM+Wi12rtuUwghHpbJbOK3pF9J06eSmZ9BZn4mmXmZf/xb8PhS\n6kV2x+1ErVIz238O01u9gsZBY+3SH4nc8lVCmjRpys8//whASkoya9Z8CEDlyl5cuRKL2WzmxIlf\n7ljnr9Nq6vV6ZsyYgtlstkyr2bBhY44f/4Xc3FzMZjPvvbcCvT6XWrVqc+7crwCWQ9FF4exckaSk\nJMxmM0lJidy4ce2er23YsDFnzpzCYDCQnJzEG2+8CvC3IK9ZszbXrl0hOzsLgBMnjtOwYZMi1ySE\nEPdjNpvZcXkb3b97gm7fdSRoSz/GbB/Bi3vG8+qPL/POoTmsOLaEj099wO64nbTybs3ep35iZpvZ\nNh/YYON72mVZ9+6BHD9+lBdfHIfRaGTcuIJD05MmTeHNN2dTtWo1y3nw//rrtJoAI0aMumNazX/9\n6xOGD3+aqVMnolKp6Ny5K1qtE0899TRvvfU6Bw9G4Otbv8g1urq60rFjRyZMGEu9evXve/V3tWrV\n6d27H9OmTcJsNvPCC1MBaNCgIRMnjmXy5JcsPUyd+jIzZ05HUVQ0b96SFi1acuxY5AN9/4QQ4q/M\nZjMRV/exJHI+JxNOoKAwyHcI9dzro1O7oFPr0Gl0BV9rdOjUOlw1rtSpVBeVYj/7pzLLVyFsaYaa\nhyH92TZ77w/sv0fpr3CHrv/M4qj5RMYfBmCQ7xBea/sGDT0aFUeJj6w0Z/mSPW0hhBBl0rGbUSyJ\nWsjBaxEA9KnTj9f8g2lWubmVK7MeCW0hhBBlSr4xn9d+nMHGc18B0LVmd173f5PWVdpYuTLrk9AW\nQghRZmTnZzNx97PsidtFc6+WzA9YTIfqMqbDf0loCyGEKBNSc1MYvX04R29G0r1WIOt6f0VFdUVr\nl1WmSGgLIYSwuptZ8YzYOoTfkn9laP1hrOr+sV3colXc7Oc6eCGEEDbpUloMA0J78Vvyr4xvNomP\nAj+VwL4H2dMWQghhNWcSTjHih6Ek5iQwq20wM9vMRlEUa5dVZkloCyGEsIpD13/mmR0jyczLYGnn\nlTzfdIK1SyrzJLSFEEKUuq0xW5iydwIms4lPen3O4HpDrV2STZDQFkIIUSrMZjN74nay6vg/ibp5\nBGfHinzVbwNda3a3dmk2Q0JbCCFEiTKYDGy5GMqq4//kt+RoAHrV7sPr7d6iaeVmVq7OthQptBct\nWsSpU6dQFIXg4GCaN/9zCLm9e/eyevVqNBoN/fv3Z8yYMfz73/8mPDzc8pqzZ89y4sQJnnnmGbKz\nsy1zLc+ePZumTZsWc0tCCCHKglxDLh8f28CSn5YSlx6LSlExtP5TTG/1Cn6V5Xf/wyg0tKOiooiL\niyMkJISYmBiCg4MJCQkBwGQyMX/+fDZv3oybmxsTJ04kMDCQp556iqeeesqy/o4dOyzbW7x4MQ0a\nNCihdoQQQlhbvjGfNac/4uNTH3A7+xZaBy3P+o1nasuXqFPpMWuXZ9MKDe3Dhw8TGBgIgK+vL2lp\naWRmZqLT6UhJScHV1RUPDw8A2rdvz6FDhxg69M8LCj788ENWrFhRQuULIYQoS9L1aYzbNZaD1yLQ\nqV2Y1XEWz9SfQJWKVa1dml0oNLQTExPx8/OzPPbw8CAhIQGdToeHhwdZWVnExsbi4+NDZGQk/v7+\nlteePn2aatWq4eXlZXlu1apVpKSk4OvrS3BwME5OTvd8b3d3ZxwdHR62t2Jzv2nS7IH0Z9vsvT+w\n/x7tpb9r6dcYsqkfZ26fYWCDgawPWo97BXdrl1UqSuszfOAL0f46/baiKCxZsoTg4GBcXFyoUaPG\nHa/dtGkTQ4YMsTweO3YsDRs2pFatWsydO5cNGzYwfvz4e75XSkr2g5ZX7GSuW9sm/dk+e+/RXvo7\nm3iGUduGcTMrnuebTmDRE8sxZDpABeyiv/spzfm0Cx3G1Nvbm8TERMvj27dv37Hn7O/vz8aNG1mz\nZg0uLi74+PhYlkVGRtKqVSvL4549e1KrVi0Aunfvzvnz5x+sEyGEEGXO/it7GbS5Dzez4pnbYQFL\nOr2Lg8r6R0ntUaGhHRAQwK5duwCIjo7G29sbnU5nWT5hwgSSkpLIzs4mIiKCDh06AHDr1i0qVqyI\nRlMwfqzZbOa5554jPT0dKAj0+vXrF3tDQgghSs+GX79k9LanyDfl8Wmv9Uxt9ZIMQ1qCCj083rp1\na/z8/Bg5ciSKojB37lxCQ0NxcXGhZ8+eDB8+nHHjxqEoCpMmTbJclJaQkGD5GgoOpQ8fPpznnnuO\nChUqUKVKFaZPn15ynQkhhCgxZrOZpVELWPnLcjycPFjf91vaVWtv7bLsnmL+60nqMqYsnAexl/NN\n9yL92TZ77w/sv0db7C/PmMeMiKlsOh9Cbdc6fDvge3zd7n7k1Bb7e1CleU5bRkQTQghRZJl5GTy3\ncwwHr0XweJU2fNXvOypXqGztssoNCW0hhBBFkpiTyKgfnuRkwgn61OnHxz0/w1ntbO2yyhUJbSGE\nEIW6mnGF4VuDiEm9yNONxvBu11U4qiRCSluhV48LIYQo384l/0b/0J7EpF5kWqsZvNftQwlsK5Hv\nuhBCiHs6ejOS0dueIlWfytwOC5ja6iVrl1SuSWgLIYS4q31xuxm36xnyjHms6r6akY1GW7ukck9C\nWwghxN/8+/dveTliCo6KI1/03UjvOn2tXZJAzmkLIYT4C6PJyKrjK5m6bxLOjhX5btAWCewyRPa0\nhRBCAPBb0q/848A0frl1DG/nKoQM2Ixf5abWLkv8hYS2EEKUc7mGXN47voJVx1diMBkYWn8Y8wOW\n4uXsVfjKolRJaAshRDl2JP4wMyOmcyH1PD66GizrvJKedfpYuyxxDxLaQghhRyLjj/D6wZnUcq1N\ns8rNaVq5Oc0qN6e6zueO2bfS9WksOPIOX0SvQ0FhfLNJzGk3F53m3uNeC+uT0BZCCDuRY8hh+r4X\niE2/THTSGXZc/sGyzMPJA7//BnjF6nx4chXxWTdo6N6Ild3+Rduq7axYuSgqCW0hhLATK44uITb9\nMlNavsTkFtM4k3iKMwmnOZN4mrOJp/np2gF+unYAALVKzWtt3+Cl1v9A66C1buGiyCS0hRDCDpxJ\nPM1HJ1dRy7UOs9oG46x2pkrFqgTW7m15Tbo+jeiks1xIOU+H6gHUd29gxYrFw5DQFkIIG2c0GZkZ\nMR2j2ciKLu/dc+YtV20lOlQPoEP1gFKuUBQXGVxFCCFs3NozqzmZcIKnGoyka83u1i5HlCAJbSGE\nsGFX0uNYErkATydP/i9gsbXLESVMDo8LIYSNMpvNvPbjDLIN2Szv8h6eFTytXZIoYbKnLYQQNur7\nC98RcXUf3Wr2YFiDEdYuR5QCCW0hhLBBSTlJvPXz6zg7OrOsyz/vGDhF2C8JbSGEsEFzDwWTlJvE\nLP851HatY+1yRCmR0BZCCBtz4Op+vvv9G1p4tWJS88nWLkeUIrkQTQghSsmFlPO8+uPLJOckoVJU\nqBQHNGpHzEZwUDmgoMJB5YCb1o1qFasX/Kerbvm6uq46KsWB136cgYPiwMquq3BUya/x8kQ+bSGE\nKAWJOYk8vW0YV9Jj8XDywGQ2YTSbMGPCaDJiNBkx/fG1GfM9t6N10KI36pna8mWaebUoxQ5EWVCk\n0F60aBGnTp1CURSCg4Np3ry5ZdnevXtZvXo1Go2G/v37M2bMGCIjI3n55ZepX78+AA0aNOCtt94i\nPj6eWbNmYTQa8fLyYvny5Wg0mpLpTAghyohcQy7P7niaK+mx/OPx13i93VuWZV5eLiQkZFgem81m\n0vSpxGfFE591nfjMeG5kXedmVjzxmTe4kXUDzwqVea3tG9ZoRVhZoaEdFRVFXFwcISEhxMTEEBwc\nTEhICAAmk4n58+ezefNm3NzcmDhxIoGBgQD4+/uzatWqO7a1atUqRo0aRd++fVm5ciWbNm1i1KhR\nJdCWEEKUDSaziZf3T+bozUiG1HuS2f5v3vf1iqLg5uSOm5M7jT2blFKVwlYUeiHa4cOHLUHs6+tL\nWloamZmZAKSkpODq6oqHhwcqlYr27dtz6NChe24rMjKSHj16ANCtWzcOHz5cHD0IIUSZtezoIjZf\n/J62VdvxfvfVcmuWeCSF7mknJibi5+dneezh4UFCQgI6nQ4PDw+ysrKIjY3Fx8eHyMhI/P398fHx\n4eLFi7z44oukpaUxbdo0AgICyMnJsRwO9/T0JCEh4b7v7e7ujKOjwyO2+Oi8vOx7Unjpz7bZe39g\nuz1+eepLVh5bRl33umwbsxWvil53fZ2t9ldU9t4flF6PD3whmtn85wUSiqKwZMkSgoODcXFxoUaN\nGgDUqVOHadOm0bdvX65evcrYsWPZvXv3PbdzLykp2Q9aXrH73/NN9kb6s2323h/Ybo+Hrv/MhK0T\nqKR146s+30G2EwnZf+/DVvsrKnvvD4q/x/v9AVDo4XFvb28SExMtj2/fvo2X159/Lfr7+7Nx40bW\nrFmDi4sLPj4+VKlShX79+qEoCrVq1aJy5crcunULZ2dncnNzAbh16xbe3t6P0pcQQpRJMakXeG7n\nKMyY+az3VzJvtSg2hYZ2QEAAu3btAiA6Ohpvb290Op1l+YQJE0hKSiI7O5uIiAg6dOhAeHg469at\nAyAhIYGkpCSqVKlCx44dLdvavXs3nTp1KomehBDCapJykhi17SlS9am822UVnWp0sXZJwo4Ueni8\ndevW+Pn5MXLkSBRFYe7cuYSGhuLi4kLPnj0ZPnw448aNQ1EUJk2ahIeHB927d+fVV19l37595Ofn\n884776DRaJg+fTqzZ88mJCSE6tWrExQUVBo9CiFEqdAb9Ty3cxSX0y7xcuuZPN14jLVLEnZGMRfl\n5LKVlIXzIPZ+Pkb6s2323h/YTo83s+J5cc94Dt34mUG+Q/ik1+eolMJHiraV/h6WvfcHpXtOW0ZE\nE0KIR7T/yl6m7ZtEYk4i/R4byL96fFykwBbiQUloCyHEQzKYDCyJXMCqEytRq9QsfGIpE5q9KPdi\nixIjoS2EEA/hRuZ1Xtgzjsj4w9R2rcPaXl/Q0ru1tcsSdk5CWwghHtDeuF1M2/cCybnJDPIdwsqu\nq3DVVrJ2WaIckNAWQogiyjfmsyjy//jw5PtoHbQs7byS5/zGy+FwUWoktIUQoggMJgOjtg3jx2sR\n1K3ky9re62lWuXnhKwpRjCS0hRCiCOYfnsuP1yLoUasna3t9gU5j/+Npi7JH7kkQQohChF34ntWn\n/kU9t/p80utzCWxhNRLaQghxH78l/cqMiKlUVOv4os9GXDSu1i5JlGNyeFwIIe4hTZ/KcztHkW3I\n5rPeX9PAo6G1SxLlnOxpCyHEXZjMJqbuncTltEu81OofDPAdZO2ShJDQFkKIu1l5bBm743bSuUY3\n3mj3lrXLEQKQ0BZCiL/ZE7uT5UcXU0NXkzU9P8NB5WDtkoQAJLSFEOIOl9JimLJvEhoHDZ/3+RrP\nCp7WLkkICwltIYRdyDXkcj3j2iNtIys/i+d3jCFNn8ryLu/RwrtVMVUnRPGQ0BZC2Lwbmdfpvakr\nrb/yY8reicSlxz7wNtL1aby8fwq/JUfznN94RjYaXfyFCvGIJLSFEDbt9+Rz9A/tyW/Jv1KtYnU2\nnQ+h48bHmfPTLBJzEgtd/0p6HG/95w1aftmE8JjNtKniz4InlpZC5UI8OAltIYTNiow/wsDNvbie\neY0328/j+NhoVgd+SjWdD2vPfEzbr5uz/OhiMvMy/rbu8VvHmLjrOfw3tGDNqQ+pqK7InHZzCRkY\nisZBY4VuhCicDK4ihLBJOy5v44Xdz5NvymdV99WWw9lPNhjOQN8gvvr1c949tozlRxfz+dm1/OPx\nWYxu8iz7r+xl9cl/EXXzCAB+ns14scVUhtQfJmEtyjzFbDabrV3EvSQk/P2v49Lm5eVSJuooKdKf\nbbP3/uDuPX4Z/TmzDr6Ck4MT63p/SY/ave66bmZeBh+f+pAPT64iKz8TrYMWvVEPQGCtXkxuOZ0n\nfDpbdWpNe/8M7b0/KP4evbzuPba97GkLIWyG2WxmxbElLD+6GE8nTzb0/zetq7S55+t1Ghdebfs6\nz/qN571flrPj8ja61erBpOZTaOjRqBQrF6J4SGgLIWyC0WRk1sF/8NWvn1PLtQ7fDQilrlu9Iq3r\n5ezFwk7LWNhpWQlXKUTJktAWQpR5JrOJSXueZ2tMGM0qt2DjgE1Uca5i7bKEKHUS2kKIMm/t6dVs\njQmjQ/UAvu4XItNjinKrSKG9aNEiTp06haIoBAcH07x5c8uyvXv3snr1ajQaDf3792fMmDEALFu2\njF9++QWDwcALL7xAr169eP3114mOjsbNzQ2A8ePH07Vr1+LvSghhN07fOs38w3OpXKEya3utl8AW\n5VqhoR0VFUVcXBwhISHExMQQHBxMSEgIACaTifnz57N582bc3NyYOHEigYGBxMbGcuHCBUJCQkhJ\nSWHIkCH06lVwdec//vEPunXrVrJdCSHsQq4hl9Fho8kz5fFetw/xdva2dklCWFWhoX348GECAwMB\n8PX1JS0tjczMTHQ6HSkpKbi6uuLh4QFA+/btOXToEIMHD7bsjbu6upKTk4PRaCzBNoQQ9mjBkbmc\nvX2W55tOoFedvtYuRwirK3REtMTERNzd3S2PPTw8SEhIsHydlZVFbGws+fn5REZGkpiYiIODA87O\nzgBs2rSJzp074+BQMLXd119/zdixY3nllVdITk4uiZ6EEHZg/5W9fHJ6NY0qN2JuhwXWLkeIMuGB\nL0T761gsiqKwZMkSgoODcXESSyW6AAAgAElEQVRxoUaNGne8du/evWzatInPPvsMgMGDB+Pm5kbj\nxo355JNP+OCDD3j77bfv+V7u7s44Olp/Htv73ehuD6Q/22aP/SVkJTDjwBTUKjUbh26kdjX7vlLc\nHj/Dv7L3/qD0eiw0tL29vUlM/HPQ/du3b+Pl5WV57O/vz8aNGwF499138fHxAeCnn37i448/5tNP\nP8XFpaCZDh06WNbr3r0777zzzn3fOyUlu+idlBB7H81H+rNt9tif2Wzm2R3PcTPzJm93mE+raq3s\nrse/ssfP8K/svT8o3RHRCj08HhAQwK5duwCIjo7G29sbnU5nWT5hwgSSkpLIzs4mIiKCDh06kJGR\nwbJly1izZo3lSnGA6dOnc/XqVQAiIyOpX7/+QzclhLBPX/36BTtjt/OET2emtJxu7XKEKFMK3dNu\n3bo1fn5+jBw5EkVRmDt3LqGhobi4uNCzZ0+GDx/OuHHjUBSFSZMm4eHhYblqfMaMGZbtLF26lNGj\nRzNjxgwqVKiAs7MzixcvLtHmhBC25ULKed76z+u4ad34V/ePUSkyEaEQfyUThhTC3g/tSH+2zZ76\nyzPm0S80kNMJJ/m013oG1RsC2FePdyP92b4ydXhcCCFKw7KoRZxOOMnIRqMtgS2EuJMMYyqEKFX5\nxnwupl4gOukMvyZFE514huiks9zOvkVt1zosekIm9RDiXiS0hRAlLjL+CF//+gXRSWc5n3yOPFPe\nHct9dDXoU6cfr7d7C53G/m8PEuJhSWgLIUpMfOYN5h1+i9AL/waggmMF/Co3pYlnU/w8C/5t4umH\nm5N7IVsSQoCEthCiBOQacvn41Ae898u7ZBuyaOHVinkdF9KuWgccVNYfMEkIWyWhLYQoNmazmV2x\nO3jrP68Tlx5L5QqVWfjEUp5uPEZu3xKiGEhoCyGKxfnk33nzP7M5cHU/jipHXmgxlVfbzKaS1q3w\nlYUQRSKhLYR4ZCuPLWPFsSUYTAa61uzOgoClNPBoaO2yhLA7EtpCiEey+uQHLIlaQA1dTRZ1Wk7v\nOn1RFMXaZQlhlyS0hRAPLfTCv5l7KJiqFauxZcgOarrUsnZJQtg1uTJECPFQfrwawfR9L+KqqcS3\nA0IlsIUoBRLaQogHdibhFM/tHI2Cwpd9v6GJp5+1SxKiXJDD40KIBxKbdpmRPzxJdn4Wn/ZeT0ef\nJ6xdkhDlhoS2EKLIErITGPHDEBJybrO403IG+gZZuyQhyhU5PC6EKJLM/EzGbH+Ky2mXmNH6VcY3\ne8HaJQlR7khoCyEKlW/MZ8KusZy4fZyRjUbzRru3rF2SEOWShLYQ4r4y8zKYvv9F9l/ZS2CtXrzb\nZZXchy2Elcg5bSHEXeUZ8/gy+jNW/rKMxJxEWns/ztre61E7qK1dmhDlloS2EOIOJrOJzRc2sSRq\nAXHpsVRU65jVNpgXW06jorqitcsTolyT0BZCAAUzdEVc3cuCI/M4m3gatUrNxGYvMuPx1/By9rJ2\neUIIJLSFEMDxW8dYcOQdfr5+EAWFYQ1GMNt/DrVd61i7NCHEX0hoC1HOmMwmzqf8TmT8YY7cOERk\n/GGuZV4FILBWL+a0fwe/yk2tXKUQ4m4ktIWwcyazieO3jhEZf4TI+IKQTtGnWJZ7OHnQ77GBTGo+\nWUY3E6KMk9AWwo6l69N4budofr5+0PJcLZfaBNbuTfvqHWlXtQP13RvILVxC2AgJbSHs1K2sm4z8\n4Umik87QvVYgIxqOol21DlTX+Vi7NCHEQypSaC9atIhTp06hKArBwcE0b97csmzv3r2sXr0ajUZD\n//79GTNmzD3XiY+PZ9asWRiNRry8vFi+fDkajaZkOhOiHLuUepHhW4dwJSOO5/zGs7jTChxUDtYu\nSwjxiAodES0qKoq4uDhCQkJYuHAhCxcutCwzmUzMnz+ftWvXsmHDBiIiIrh58+Y911m1ahWjRo1i\n48aN1K5dm02bNpVcZ0KUUydvH2fA5l5cyYhjtv8clnZeKYEthJ0oNLQPHz5MYGAgAL6+vqSlpZGZ\nmQlASkoKrq6ueHh4oFKpaN++PYcOHbrnOpGRkfTo0QOAbt26cfjw4ZLqS4hy6cDV/QSF9Sc5N5kV\nXd5nZpvZcr5aiGKmpCTjtPErKg0PonKdanDgQKm9d6GHxxMTE/Hz+3OCew8PDxISEtDpdHh4eJCV\nlUVsbCw+Pj5ERkbi7+9/z3VycnIsh8M9PT1JSEgogZaEKJ9CL/yb6fteRKWoWNf7K/rXHWjtkoSw\nG0p6Gpod29BuCUXzYwRKfj4A+a0fR12zZqnV8cAXopnNZsvXiqKwZMkSgoODcXFxoUaNGoWuc7/n\n/pe7uzOOjtY/rOfl5WLtEkqU9GfbvLxceO/Ie7yy5xUqaSsR/nQ4nWt3tnZZxao8fIb2zGb7y8iA\n8HD47jvYuRPy8gqeb9UKhg+H4cNR160LQGmNGVhoaHt7e5OYmGh5fPv2bby8/izP39+fjRs3AvDu\nu+/i4+ODXq+/6zrOzs7k5ubi5OTErVu38Pb2vu97p6RkP3BDxc3Ly4WEhAxrl1FipD/bZTKbuKT/\nlY8Or+Hr39ZTxbkq3w4IpbFzU7vq2Z4/Q5D+ypysLLR7dqLdshnNvt0oubkAGBr7oR88BP3gIRh9\n6//5+oSMYu/xfn/kFHpOOyAggF27dgEQHR2Nt7c3Op3OsnzChAkkJSWRnZ1NREQEHTp0uOc6HTt2\ntDy/e/duOnXq9EiNCVHe5Bpy2RO7k5kHXqLZFw3o+FlHvv5tPb5u9dg2dI+MZCbEw8jJQfNDOC4T\nn6Oyny+uk55Huy0cY81aZL36Osk/RZHy42Gy/zHrzsC2gkL3tFu3bo2fnx8jR45EURTmzp1LaGgo\nLi4u9OzZk+HDhzNu3DgURWHSpEl4eHjg4eHxt3UApk+fzuzZswkJCaF69eoEBQWVeINC2LqU3GR2\nx+5kZ+x2Iq7sI9uQBYCnkyfPt3yertV60bVmdyo4VrBypULYEL0eTcQ+tGHfo9m1A1VWwQXWhrq+\n6IOGoh80FGPjJlDGLuRUzEU5uWwlZeGQis0d2nlA0l/Ztu3SVqbsnUCOIQeAupV86fNYf/o81p+2\nVfypWsXNpvsrClv/DAsj/ZWivDw0ByPQhoWi2bENVUY6AMZaddAHDSV38FCMTZs9cFCX5uFxGRFN\niDLq23MbmBExFSeHCsxpN5e+jw2QIUeFeFD5+ah/Poh2Syja7VtRpaYCYKxRk+xnnkM/eAiGlq3L\n3B71vUhoC1EGrT29mjk/z8Zd6843A76ndZU21i5JCNthNKI+9DPasFC027agSk4ueLpadbJHjEI/\neCiGx9vaTFD/lYS2EGWI2WxmxbElLD+6mCrOVfluYBiNPZtYuywhyj6jEXXUEbRh36PdugVVYsE4\nIEbvKuSMn0Tu4Ccx+LcDVaHXX5dpEtpClBEms4m3//MGn5xeTS3XOmwauIU6lR6zdllClF0mE45H\no9CGh6IND8Ph1s2Cpz09yXl2PPrBQ8jvEAAO1h/vo7hIaAtRBhhMBv5xYDrfnttAI4/GfDcwjKoV\nq1m7LCHKHrMZx+PH0G7ZjHZrGA7XrwFgcncnZ8yz6AcNIf+JzuBon/Fmn10JYUP0Rj0v7B7H9stb\nae39OBsHbMLDydPaZQlRdpjNOJ4+WRDU4ZtxuBIHgMm1ErkjR6MfPIS8zt1ArbZyoSVPQlsIK8rI\nS+f5nc9w8FoEnXy6sL7vRnQaGx3yUYjiZDbjEH0Wpy2haLeE4hB7GQCTzoXcYSPQDx5KXtfuoNVa\nudDSJaEthBUYTUY2nvuKxZHzScxJoM9j/fmk5+c4OTpZuzQhrMrh3G8Ft2dtCcXx4gUAzM4VyR3y\nJPrBT5LXPRCcyu//JxLaQpSyA1f3M/c/c/gtORpnx4rM9p/Dy61n4qiS/x1F+eRw8cKfQX3uNwDM\nFSqgHxhEbtBQ8nr0AmdnK1dZNshvCSFKye/J55h36E32XtmNgsKoRs/wers35YIzUS6pLl9CG74Z\np7BQHKPPAGDWatH3HVAwjGjPPvCXeS5EAQltIUpYYk4iy48u4svozzGajTzh05l5AYtoVrm5tUsT\nolSprsShDQ9DuyUU9akTAJjVavS9+hSco+7TD7OLq5WrLNsktIUoIdn52Xx6Zg3vH3+XjLx0fN3q\n8U7HhfSq3UeGIhXlx9WrVPj8a7Thoah/OQaA2dGRvO6B5AY9SV7f/pgruVm5SNshoS1EMcs35rPx\n3FesOLqEW9k3cde6s+iJZTzrNx61g/3fkiKE6mY82q1haMNC4WgkOsCsUpHXuVvBoe9+AzB7yG2N\nD0NCW4hiYjKbCLv4PUujFnI57RLOjs7MaP0qU1u9RCWt7EkI+6bcvo32hy0Fh76PHEIxmzErCnTt\nSka/wej7D8Ls5WXtMm2ehLYQj8hsNrPvym4WHvk/opPOoFapGdd0Iq+0mUUV5yrWLk+IEqMkJaHd\nFo52y2bU/zmIYjIBkN+uA7mDh5A3MAjPpvXJLStTc9oBCW0hHkFk/BEWHnmHI/GHUFAY1mAEs9oG\ny5jhwm4pqSlodmzDKex71AcPoBiNAOQ/3rbg0PfAIEzVfaxcpf2S0BbiIZy49QtLjy5k/5W9APSu\n05c32r1NE08/K1cmRPFT0tPQ7NiGNnwzmgP7UfLzAchv1Rr9oKHoBwVhqlnLukWWExLaQjyAs4ln\nWBa1kJ2x2wHo5NOF2f5v4l+tnZUrE6J4KZkZaHbtQLtlM5r9e1Dy8gDIb9YC/eA/grqOHFEqbRLa\nQhTB78nnWHZ0EVtjwgDwr9qe19u9yRM+na1cmRDFKCsLzb7dOIWFotm7CyU3FwBDYz/0g4egHzwE\no299KxdZvkloC3EfMakXWH50CZsvbMKMmVberZnt/ybdavaQe62FfcjJQbNvT8Gc1Lt3omRnA2Co\n36Bgj3rwUIwNG1m5SPFfEtpC3EWuIZflRxfz0clVGM1GmlZuzmz/OTIwirAPej2aiH1ow75Hs2sH\nqqxMAAyP1S24mGzwkxgbNwH5WS9zJLSF+B/Hbkbx8v4pXEg9Ty3XOsztMJ/+dQeiUlTWLk2Ih5eX\nh+ZgBNqwUDQ7tqHKSAfAWKs22eMmog8aiqFpcwnqMk5CW4g/5BhyWBq1kI9PfYDJbGJCsxcIbj8X\nnVomLRA2Kj8f9c8HC2bQ2r4VVWoqAEafGmSPebYgqFu2lqC2IRLaQgBR8ZG8HDGZmNSL1HF9jPe7\nf0SH6gHWLkuIB2c0oj70M9qwULTbtqBKTi54umo1sic9jX7wUAyPtwWVHDmyRRLaolzLzs9mcdR8\nPjn1EQAvNJ/CG+3exlktc/cKG2I0oo46gjbse7Rbt6BKTADA5OVNzriJ6IOeJN+/vQS1HShSaC9a\ntIhTp06hKArBwcE0b/7nlIIbNmwgPDwclUpF06ZNmTNnDqtXr+bQoUMAmEwmEhMT2bVrF927d6dq\n1ao4ODgAsGLFCqpUkWEeRenLzs9mV+x2lkQt4HLaJepW8uX97qtpV629tUsTomhMJhyPRhVc9R0e\nhsOtmwVPe3qSM3Yc+qCh5HcIgD9+3wr7UGhoR0VFERcXR0hICDExMQQHBxMSEgJAZmYm69atY/fu\n3Tg6OjJu3DhOnjzJ5MmTmTx5MgCbN28mKSnJsr21a9dSsWLFEmpHiHvLN+Zz8FoE31/4N9sv/UC2\nIQsFhcktpjPbf47sXYuyz2zG8fgxtFs2ow3fjMON6wCY3NzIGT0W/eCh5D/RGRzlIKq9KvSTPXz4\nMIGBgQD4+vqSlpZGZmYmOp0OtVqNWq0mOzsbZ2dncnJyqFSpkmVdg8HAN998w5dffllyHQhxH2az\nmaj4SEIvfEd4zGYScxIBqOVahyfrT2ZYg5HUd29g5SqFuA+zGcfTJ/8M6itxAJhcK5E7YhT6oKHk\nde4Gapn2tTwoNLQTExPx8/tzPGUPDw8SEhLQ6XRotVqmTp1KYGAgWq2W/v3789hjfw5rt3v3bp54\n4gmcnJwsz82dO5fr16/z+OOPM3PmTLnnVZQIs9nMp2c+Zu3Z1cSmxgJQuUJlxjebxJP1h/N4lbby\nsyfKLrMZh+izaMM3o90SiuPlSwCYKurIfXI4+qAnyevaHbRaKxcqStsDH0Mxm82WrzMzM1mzZg07\nd+5Ep9Px7LPPcu7cORo1Khg95/vvv2fevHmW17/00kt06tSJSpUqMXXqVHbt2kWfPn3u+V7u7s44\nOlr/fIyXl4u1SyhR9tjf4p8WM+fnYHQaHWNbjGVU01H0qNsDR5X9HTa0x8/vf9l7j5b+fv0VQkIK\n/vv994LnKlaEkSNh+HBUffrgVKECTvfeVJlk758flF6Phf4G8/b2JjEx0fL49u3beP0xkXlMTAw1\na9bEw8MDgDZt2nD27FkaNWpEdnY2N2/epEaNGpZ1g4KCLF937tyZ8+fP3ze0U1KyH7yjYubl5UKC\nHc8Fa4/9rTvzCcE/BVNDV5NDE/6DU54bAClJOVaurPjZ4+f3v+y9R6+UeLI++7Jgj/rcbwCYK1Qg\nb2AQuUFDyevRC5z/uN4i0wCZtvW9sPfPD4q/x/v9AVDo9f8BAQHs2rULgOjoaLy9vdHpCgab8PHx\nISYmhtw/BpU/e/YsderUAeDcuXPUrVvXsp2MjAzGjx9P3h8zxRw9epT69WXgeVG8/v37t7zx06t4\nVfBm06At1KxU09olCfE3qsuXqPD+u7h3C4CGDam4dCEOly+h7zuA9DWfkRgdQ/q6L8kbGPRnYAtB\nEfa0W7dujZ+fHyNHjkRRFObOnUtoaCguLi707NmT8ePHM3bsWBwcHGjVqhVt2rQBICEhwbIHDuDi\n4kLnzp0ZMWIEWq2WJk2a3HcvW4gHtf3SD7y0fzKVtG58NzCMum71rF2SEBaqq1cKLibbEor61AkA\nzGo1DBhAet9B5PXph9nF1cpVirJOMf/1JHUZUxYOqdj7oR176e/gtQOM+mEYjio1mwZtoU1Vf8B+\n+rsXe+8PbLtH1fVraLeGFQT1L8cAMDs6kt+5K7lBT5LXtz+V69W02f6KwpY/v6IqzcPj9ndVjih3\njt2MYuz2pwH4st83lsAWwhpUN+P/COrNqKOOAGBWqcjr3K1gBq1+AzB7eFq5SmGrJLSFTYtOPMvT\n24ahN+ayrvdXdK7R1doliXJIuX0b7Q9b0IZvRn34PyhmM2ZFIS+gU8Gc1P0HYf7jAl4hHoWEtrBZ\nl1IvMnxrEGn6VD7osYZ+dQdYuyRRjihJSWi3hRfsUf/nIIrJBEC+f/uCq74HBmGqUtXKVQp7I6Et\nbM7ltEtsjQlj3ZlPSMi5zeJOKxje8GlrlyXKASU1Be32HwrOUR88gGI0ApD/eNuCQ98DgzBV97Fy\nlcKeSWgLm3Ap9SLhMWGEx4RxNvE0AI4qR97uMJ/xzSZZuTphz5T0NDQ7tqEN34zmwH6U/HwA8lu2\nQj/4SfSDgjDVrGXdIkW5IaEtyqx7BXWPWj0Z5DuEPo/1w93Jo5CtCPHglMwMNLt2oN2yGc3+PSh/\njC+R36wF+sFD0A8agqnOY4VsRYjiJ6EtyhyDycDc/wSz9szHAKhVagJr9WJQvSH0qdMPNyd3K1co\n7FJWFpp9u3EKC0WzdxfKH4NGGRr7FQT14CEYfWVAKGFdEtqiTMnMy2DS7ufZe2U3DdwbMq3VDAlq\nUXJyctDs21MwJ/XunSjZBUMnG+o3KLjqe/BQjA0bWblIIf4koS3KjGsZVxm9bTi/JUfTrWYP1vb6\nAldtpcJXFOJB6PVoIvah3RKKZud2VFmZABgeq1twMdmgoRib+IHMAifKIAltUSYcv3WMZ7aPJCHn\nNs83ncDCJ5bZ5Yxcwkry8tAcjEAbFopmxzZUGekAGGvVJnvcRPRBQzE0bS5BLco8+a0orG5rTBhT\n904iz5THwieWMqHZizLXtXh0BgPqn35EuyUU7fatqFJTATD61CB7zLMFQd2ytQS1sCkS2sJqzGYz\nq46vZGHkPCqqdXzV+0t61pFJZMQjMBpRH/oZbVgo2u3hqJKSCp6uWo3sSU+jHzQUQ5u2oCp0gkMh\nyiQJbWEVecY8Xv3xZb49t4HqFX34uv93NK3czNplCVtkMqGOPFywR711C6qE2wVPe3mTM24i+qAn\nyfdvL0Et7IKEtihRWflZXEqLISblAjFpF7mYcoGY1AvEpMWQkZdOS69WfNUvhCoVZbhH8QBMJhyP\nHS246js8DIeb8QVPe3qS8+x49IOHkN8hABwcrFyoEMVLQlsUu1xDLrMOvsJP137keua1vy3XqDTU\ndfOlY/URvN1hPs5qZytUKWyO2YzjiV8K5qQO34zD9YKfLZO7OzljnkU/aAj5T3QGR/m1JuyX/HSL\nYmUym5i27wXCYzbjVcGbTj5d8HWrRz23+vi61cPXrT41XWrhoJI9IFEEZjMcP07FL75Gu2UzDldi\nATC5ViJ3xCj0QUPJ69wN1Grr1ilEKZHQFsVq/uG5hMdspn21jnw3MAwnRydrlyRsjdmMw6/RBeeo\nt4TC5Us4A6aKOnKfHI4+6EnyunYHrdbalQpR6iS0RbH57OxaPjz5PvXc6rO+70YJbPFAHH4/hzbs\ne7Thm3G8cB4As7MzjBhBWp9B5HUPhAoVrFylENYloS2Kxa7YHQT/9BqVK3ixsf8mmchDFIlDzIWC\n27O2hOJ47jcAzE5O6AcMLpiTOrA3XrWrkJeQYeVKhSgbJLTFIzt5+zgv7H4erYOWDf2+o04lmf1I\n3Jvq8iW04ZtxCgvFMfoMAGaNBn2f/gXnqHv1waxzsXKVQpRNEtrikVxJj2P0tuHkGnP5os9GWlV5\n3NoliTJIdfVKwVXfW0JRnzoBgFmtRt+zN/rBQ8nr0w+zq4wzL0RhJLTFQ0vNTWHUtmEk5Nxmcafl\n9Hmsn7VLEmWI6sZ1tOF/BPUvxwAwOzqS1z2Q3MFDyevbH7ObzN4mxIOQ0BYPRW/U89zO0ZxP+Z3J\nLaYzvtkL1i5JlAGqWzfRbA3DKSwUddQRAMwqFXmduxXMSd1/IGYPTytXKYTtktAWDywrP4uZB17i\n0I2fGegbxNyO861dkrAiJSEB7bbwgj3qQz+jmM2YFYW8gE7oBw1BP2AwZi8va5cphF2Q0BZFEpt2\nmb1xu9gTt4tDN35Gb9TTtmo7PuixBpUiYzqXN0pyEtptW9Fu2Yz65x9RTCYA8v3bF1z1PTAIUxUZ\nmlaI4lak0F60aBGnTp1CURSCg4Np3ry5ZdmGDRsIDw9HpVLRtGlT5syZQ2hoKO+//z61atUCoGPH\njkyePJlz587xzjvvANCwYUPmzZtX/B2JYpFnzCPq5hH2xO5ib9wuLqSetyzz82xGrzq9mdxiOhUc\n5b7Z8kJJTUGzYxtOYd+jPngAxWgEIP/xtgWHvgcNwVTdx8pVCmHfCg3tqKgo4uLiCAkJISYmhuDg\nYEJCQgDIzMxk3bp17N69G0dHR8aNG8fJkycB6NevH7Nnz75jWwsXLrSE/syZM/nxxx/p0qVLCbQl\nHtZ/p8tcdeKfZOSlA+Ds6EyfOv0IrN2bwNq9qK6TX8zlhZKehmbndrRbQtEc2I+Snw9AfstW6AcN\nRT94CKaataxbpBDlSKGhffjwYQIDAwHw9fUlLS2NzMxMdDodarUatVpNdnY2zs7O5OTkUKnS3W/b\nyMvL4/r165a99G7dunH48GEJ7TIkMz+Tl/ZN5odLW/B2rsLIhqMIrN2bDtUDZHSz8iQzE+3uHWjD\nQtFE7EXR6wEw+DUjN2howR71Y3WtXKQQ5VOhoZ2YmIifn5/lsYeHBwkJCeh0OrRaLVOnTiUwMBCt\nVkv//v157LHHOHHiBFFRUYwfPx6DwcDs2bPx9PTE1dXVsh1PT08SEhJKpivxwGLTLvPsjlH8lhxN\nx+pP8GnvL6lcobK1yxKlJSsLzb7dOIWFotm7CyU3FwBD4yYFF5MNHoqxXn0rFymEeOAL0cxms+Xr\nzMxM1qxZw86dO9HpdDz77LOcO3eOFi1a4OHhQdeuXTlx4gSzZ8/m008/ved27sXd3RlHR+vPBuXl\nZd+jM53KiGRE6AiSc5KZ1nYaK3uvRO1gP7Mm2fvn99D95eTAzp0QEgJbt0J2dsHzjRrBiBEwfDiO\nTZrgCFQstmofjnyGts3e+4PS67HQ0Pb29iYxMdHy+Pbt23j9cftGTEwMNWvWxMOjYJzpNm3acPbs\nWYYNG4avry8ArVq1Ijk5GXd3d1JTUy3buXXrFt7e3vd975SU7AfvqJh5ebmQYKfjHpvNZjbErOPV\nPa/ioDjwz64fMLrJWFKTc4Fca5dXLOz584OH6E+vR3NgP9qw79Hs3I4qKxMAw2N10QcNRT9oKMYm\nfqAoBa8vA987+Qxtm733B8Xf4/3+ACg0tAMCAvjXv/7FyJEjiY6OxtvbG51OB4CPjw8xMTHk5ubi\n5OTE2bNn6dKlC2vXrqVatWoMGDCA8+fP4+HhgUajoW7duhw7dow2bdqwe/dunnnmmWJrUjyYHEMO\nr/04g+9+/wZv5yp83udr2lZtZ+2yREnIz0dzMKLgHPWObajS0wAw1qpN9riJ6IOGYmja/M+gFkKU\nWYWGduvWrfHz82PkyJEoisLcuXMJDQ3FxcWFnj17Mn78eMaOHYuDgwOtWrWiTZs21KhRg9dee41v\nv/0Wg8HAwoULAQgODubtt9/GZDLRokULOnbsWOINijuZzCYup8Uwec8ETiacwN/Hn7U9vqSarrq1\nSxPFyWBA/fPBgjmpt29FlZICgNGnBtmjx6IfPARDq8clqIWwMYq5KCeXraQsHFKxxUM7BpOBqxlX\niE27zOX0S8SmXSb2/9u77/io6rTv45/pSUiBxCQiRSAiQVgQDCogPbEQTOMWQelB1wXRXQslKOW5\nX4oFfBQri+xzuwsKC6TRI4K6SKS4gHfQUEJJpCYQApMymfJ7/hgcRalZkpOZXO+/mDM5J9fFycx3\nzu935pyygxw+d4jDZWIGJhsAABzeSURBVIeocrqHvodGP87/G/wx50vtGldce7xx/12Pi/pzOjHl\nfuO+1eXqLPSnT7sX39wU28OJ2BIH44jpBnrvuhhOg9qHPsjX+4N6NjwuvEe5vZy/7v6A93fN41x1\n2e+eDzIH07ZJO1qFtCbu1gd4tN1j+Bn9OI/vhrbPc7ncQZ2VjmVlFvriU+7FN4VTOWYctqTB2O/p\n7nVBLYS4NAltH2B32vk0/x+8uX02pypOEuYXxiO3D6VVSGtah7ShVXBrWoW0IcwvDJ0Mh3o/lwvj\nju1YstNhVRaNjx1zLw4NpXLEGGxJKdh73AcG7b95IYS4sSS0vZhSilUHs3jl21kcLCsgwNiI52Mm\nM/7OiQSZg6++AeE9lMK48zv3PamzMzAc/cm9vEkTKh8bgS0xBft9vcHkO1/VE0L8noS2l/rm6L/4\n79zp/PvUdxj1RsZ0HMdzMZOJDIjUujRxoyiF8X93u+eoszMwFB4BwBUUTNWjj2FLTCZkcALWMpvG\nhQoh6oqEtpc5ev4nXvjqWb4o/ByAxKgUpt7zEm0a36ZxZeKGUArDD3vcc9RZ6RgPHQTA1SiQqsFD\nsCWmUN1vAFgs7p83mwEJbSEaCgltL1J47ggpWYMoPH+E+5r15uV7Z9El8i6tyxI3gGFvPpbMFViy\nMzDud99RTQUEXLjWdwrVA+LAX+6oJkRDJ6HtJQrPHSE5K56i84VM6pbG8zGT5aQyL2co2O+eo85K\nx/jjDwAoPz9sgxLdt7qMfQAaaX0BUSFEfSKh7QWOnDtMStYgis4XMuXul3guZpLWJYka0h8+hCU7\nA0tmOqa87wFQZjO2Bwe6h74feAgV6PvXaRZC1IyEdj13uOwQKVmD+MlaxNS7X+YvMS9qXZK4Tvqi\nQizZmViyVmDatRMAZTJhi3sAW0Iy1Q/Fo4IvfUtbIYT4NQnteuxw2SGSs+I5av2JaffM4Nm7nte6\nJHGN9MeOYlmZ6T6i/m47AMpgoLrfAGyJKdgGDkI1bqJxlUIIbyOhXU8dKjtIcmY8x8qP8tK9M3mm\n63NalySuQn/yBOaVmfhlZWDamguA0uup7tXHHdTxCaiwMI2rFEJ4MwnteuhgWQHJmfEcLz/Gy93/\nDxO7/FnrksRl6IqLsazOxpKVjmnLZnRKoXQ6qnvc90tQX+UWtEIIca0ktOuZfWf28sjKRI6XH2N6\n9//m6S7Pal2S+A3dmdNYVq/EkpWBafNX6FwuAOx330tVUgrVDyfhirxZ4yqFEL5IQrue2H1qJ+/v\neofsgkxcysXMHq8w/s6JWpclLtCdLcW8djV+WemYvv4SncMBgP2uGPcRdUIyrluaaVylEMLXSWhr\nSCnFxsLPeX/XPDYf/RqAO8I68nzMZB6OStS4OqE7fw7z2tVYsjMwb/oCnd19NzR75y4XgjoJV8tb\nNa5SCNGQSGhroNpZTfr+ZXy4611+POO+qEbv5v2YcOcz9G3RXy6aoiWrFUvOWiyZ6Zg3bUBnc18i\n1NHhDxeuTpaMq3UbjYsUQjRUEtp1SCnF3/IWMO/fb3G8/BgGnYGUto8w4c5n+EN4Z63La7gqKjBv\nWI9fZjrmDevRVVUB4Ihu7z6iTkzBeVtbjYsUQggJ7Tpjd9p54atn+Sx/EQHGRvyx03ie7DyeFkEt\ntS6tYaqqwvzF51iyVmDJWYeuogIAx21tfwnq6PYaFymEEBeT0K4DVruVcetHsrFwA53Du7Ao/p9y\nC00t2GyYv9yIJXMF5vVr0VvPA+Bo3QbbhRtzOO/oADI9IYSopyS0a9nJipM8vvoRvi/eRWzL+/nr\nA/9DoClQ67IajupqzF/kuOeo165Gf64MAGfLW6kYnYotKQXHHzpLUAshvIKEdi06ULqfoatSKDx/\nhMfbj+TNPm9j1Mt/ea1zODBt/hpLVjqsWUlIaSkAzluaUfHYCHdQd7lLgloI4XUkQWrJ9hNbGb56\nCKW2Ul7sNpUXYqbIWeG1yenElPsNlsx0LKuz0J8+7V7etCkVTzyFLXEwjphuoNdrW6cQQvwHJLRr\nwZqDq3jq87HYXXb+b9/3ePyOkVqX5JtcLkzbvsWSuQLLyiz0xafci28Kp3LMOGxJg2k86H7KT5dr\nXKgQQtwYEto30M9f6Zq2eRJ+Bj/+MXAJsbc+oHVZvsXlwvjddixZ6ViyMzGcOO5eHBpK5Ygx2JJS\nsPe4DwwG98/LkbUQwodIaN8Ah8oOsnzfUpbvW8qhsoPc5B/Op/HLuDOiq9al+QalMO76t3voOzsD\nw9GfAHA1bkzlYyOwJaZgv683mEwaFyqEELXrmkL71VdfZffu3eh0OtLS0ujUqZPnucWLF5OdnY1e\nr6djx45MmzYNh8PBtGnTKCwsxOl0MmnSJGJiYhgxYgQVFRUEBAQAMHnyZDp27Fg7ndWys1WlZBVk\nsGzvErad+BYAf6M/KW0fYeo9L3NrcCttC/R2SmHM+94d1FkZGAoPA+AKCqbq0cewJSZT3bsfmM3a\n1imEEHXoqqG9bds2jhw5wtKlSykoKCAtLY2lS5cCYLVaWbhwITk5ORiNRsaOHcuuXbsoKCjA39+f\nzz77jP379zN16lSWL18OwOzZs7n99ttrt6taYnfa2VCYwz/3fsbnh9dR7apGh45ezfvyyO2PMqhN\nAoHmIK3L9F5KYfjxB/cFT7IyMB4sAMDVKJCqwUOwJaZQ3W8AWCwaFyqEENq4amjn5uYSGxsLQFRU\nFGVlZVitVgIDAzGZTJhMJs/Rc2VlJSEhISQkJDBo0CAAQkNDOXv2bO12UcscLgfL9y1l7o7XOXLu\nMADRoe35r9uH8l+3D+GWQLm703/CsDffPUedlY5x/z4AVEDAhWt9p1A9IA78/TWuUgghtHfV0C4p\nKaFDhw6ex6GhoRQXFxMYGIjFYmHChAnExsZisViIj4+ndevWF63/ySefeAIcYN68eZSWlhIVFUVa\nWhp+fn6X/d1NmgRgNBpq0tcN4XQ5WfT9ImZ9NYsDZw5gNpj5U8yfeKLrE9x5850+8xWu8HANRgf2\n7YOlS+Gf/4S8PPcyPz8YPBgefRRdfDx+AQFc/q/j2mnSXx3y9f7A93uU/rxfXfV43SeiKaU8/7Za\nrcyfP59169YRGBjIqFGjyM/PJzo6GnDPd+/Zs4ePPvoIgJEjR9KuXTtatmzJjBkzWLx4MampqZf9\nXaWlFddb3g3hdDnJLsjgze2zOXB2Pya9iVEdUvlz1+dpFtQcgJISqya13Wjh4UEUF5+vk9+lP3zo\nwhF1Bqa87wFQZjPVD8ZjS0qh+v4HUYEX/vDLnVD+n9dVl/1pwdf7A9/vUfrzfje6xyt9ALhqaEdE\nRFBSUuJ5fOrUKcLDwwEoKCigRYsWhIaGAhATE0NeXh7R0dEsW7aMjRs38sEHH2C6cFZvXFycZzv9\n+/dnzZo1NeuolriUi1UFWby5fTZ7S/Mx6o080fUJnurwrNzYo4b0RYVYsjKwZKdj2rUTAGUyYYt7\nwD1H/eBAVHCIxlUKIYR3uGpo9+zZk3fffZehQ4eyZ88eIiIiCAx0Xzu7WbNmFBQUUFVVhZ+fH3l5\nefTp04eioiKWLFnCokWLsFw4aUgpxZgxY5g3bx7BwcFs3bqVtm3rz+0OiyuKGbPucbad+BaDzsCw\n6OH85a4X6XZbJ5//lHij6Y8dxbIyE0tmOqbvtgOgDAaq+w1w30Fr4CBU4yYaVymEEN7nqqHdtWtX\nOnTowNChQ9HpdMyYMYP09HSCgoKIi4sjNTWVkSNHYjAY6NKlCzExMbz11lucPXuWJ5980rOdhQsX\nMmTIEEaPHo2/vz+RkZFMnDixVpu7VvvO7OWxNY9QeO4wA1s/zPTus2jT+Daty/Iq+pMnMK/MxC8r\nA9PWXACUXk91r77YEpOxxSegwsI0rlIIIbybTv16krqeqYsj3M1Hv2bMuuGU2c5e8hrhvj4f85/0\npysuxrIqC0t2BqYtm9EphdLpsHfviS0hGdugRFRExA2u+PrI/vN+vt6j9Of96tWcti9bkr+Y5798\nBoD3BsxnSLthGldU/+nOnMayeqX7ZLLNX6FzuQCw332v+4j64SRcNzfVuEohhPBNDTK0lVK8sf1V\n5u54nRBLY/7nwcX0bNZL67LqLd3ZUsxrV+OXlY7p6y/RORwA2O+Kcc9RP5yEq1lzjasUQgjf1+BC\n2+a08ezG8aTvX8atwa34NH45bZt45xXaapPu/DnMa1djyc7AvOkLdHY7APbOXdxBnZCEq+WtGlcp\nhBANS4MK7TNVpxm99nG+Pb6FmMi7+fvAJdzkf5PWZdUfViuWnLVYsjIwb/wcnc0GgKPDH7AlJlOV\nkIyrTZTGRQohRMPVYEK72llNQsaD7CvdS0JUMu8O+Ah/o1wak4oKzNkZ+GWmY96wHl1VFQCOdtHu\nI+rEFJxtZSRCCCHqgwYT2gCNLU14PmYyL3abil7XgO+zXFWF+YvPsWSnQ846QsrLAXBE3eYO6qTB\nOKPba1ykEEKI32owoW02mFmVkqN1Gdqx2TB/uRFL5grM69eit174ekKbNlQ8nExVYgrODh3BR66n\nLoQQvqjBhHaDZLdj/noTlsx0zGtXoz9XBoCzRUsqRo3FlpRCkwG9KPeR66gLIYSvk9D2NQ4Hps1f\nu2/MsWYl+tJSAJy3NKPisRHYEpNxdI355YhajqyFEMJrSGj7AqcTU+437htzrM5Cf+EGL87Im6l4\n4ilsiYNxxHQDfQOexxdCCB8goe2tXC6M27bil7UC88osDKdOuhffFE7lmHHYkgZjv6e7BLUQQvgQ\nCW1vohTG77a7h76zMzEcPwaAKzSUyhFjsCWlYO/eE4yyW4UQwhfJu3t9pxTGXf++cE/qDAw/FQHg\nCmlM5WMjsCWmYL+vN1y4Z7kQQgjfJaFdHymFMe97LJnpWLIyMBQeBsAVFEzVkGHYEpOp7tMfzGZt\n6xRCCFGnJLTrC6Uw/PgDlqwVWLIyMB4sAMDVKJCqlEewJQ2mum9/8PPTuFAhhBBakdDWmGHfXiyZ\nK7BkZ2DctxcAFRBA1YVLiFYPiAN/udyqEEIICW1NGA4e8Ax9G3/cA4Dy88MWn4AtKQVb7APQqJHG\nVQohhKhvJLTriP7wISzZmViy0jH9724AlNmM7cF49xz1Aw+hAoM0rlIIIUR9JqFdi/Q/FV046zsd\n085/A6BMJmyx97uHvh+KRwWHaFylEEIIbyGhfYPpjx/Dkp2BJSsD045tACiDgep+A9x30Bo4CNW4\nicZVCiGE8EYS2jeA7uRJLKsy3UG9NRedUii9nupefbElJmOLT0CFhWldphBCCC8noV1DupISLKuy\n3HPUWza7g1qnw35vD/cR9aBEVESE1mUKIYTwIRLa10F35jSWNauwZKZj+uZrdE4nAPZu97jP+n44\nCdfNTTWuUgghhK+S0L6as2exLFmCX+YKTF9/ic7hAMDe9S5siYOxJSThatZc4yKFEEI0BBLal6A7\nfw7zujVYstJh0xcE2+0A2DvdiS0hGVtiMq5bW2lbpBBCiAbnmkL71VdfZffu3eh0OtLS0ujUqZPn\nucWLF5OdnY1er6djx45MmzYNu93OlClTOHbsGAaDgdmzZ9OiRQvy8/OZOXMmAO3atWPWrFm10lSN\nWK1YPl+HJTMd88bP0dls7uWdO1Men0hVQjKuNlHa1iiEEKJBu2pob9u2jSNHjrB06VIKCgpIS0tj\n6dKlAFitVhYuXEhOTg5Go5GxY8eya9cuDh06RHBwMHPnzmXz5s3MnTuXt99+m1deecUT+s8//zxf\nffUVffr0qfUmL6uiAvMXOe7vUn++Dl1lJQCO6PYXjqhTCO1xFxXF57WrUQghhLjgqqGdm5tLbGws\nAFFRUZSVlWG1WgkMDMRkMmEymaioqCAgIIDKykpCQkLIzc0lKSkJgB49epCWlkZ1dTVHjx71HKX3\n69eP3Nzcug/tqirMGzdgyU7Hsm4tuopyABxRt7nP+k4ajDO6fd3WJIQQQlyDq4Z2SUkJHTp08DwO\nDQ2luLiYwMBALBYLEyZMIDY2FovFQnx8PK1bt6akpITQ0FAA9Ho9Op2OkpISgoODPdsJCwujuLj4\nir+7SZMAjEZDTXu7mNMJf/4z/P3vcO6ce1lUFDz6KAwZgrFTJ4w6HZe64nd4uG9fXlT6826+3h/4\nfo/Sn/erqx6v+0Q0pZTn31arlfnz57Nu3ToCAwMZNWoU+fn5V1znSst+q7S04nrLu7zycsIWLUKF\nNMY2ciy2xGQcne4Enc79fIn1kquFhwdR7MPD49Kfd/P1/sD3e5T+vN+N7vFKHwCuGtoRERGUlJR4\nHp86dYrw8HAACgoKaNGiheeoOiYmhry8PCIiIiguLiY6Ohq73Y5SivDwcM6ePevZzsmTJ4moy4uP\nNGrE6R8PgV7/S1ALIYQQXkR/tR/o2bMn69evB2DPnj1EREQQGBgIQLNmzSgoKKCqqgqAvLw8WrVq\nRc+ePVm3bh0AmzZt4p577sFkMtGmTRt27NgBQE5ODr169aqVpi7LYJDAFkII4bWueqTdtWtXOnTo\nwNChQ9HpdMyYMYP09HSCgoKIi4sjNTWVkSNHYjAY6NKlCzExMTidTrZs2cKwYcMwm8289tprAKSl\npTF9+nRcLhedO3emR48etd6gEEII4St06lomlzVSH+ZBfH0+Rvrzbr7eH/h+j9Kf96vLOe2rDo8L\nIYQQon6Q0BZCCCG8hIS2EEII4SUktIUQQggvIaEthBBCeAkJbSGEEMJLSGgLIYQQXkJCWwghhPAS\nEtpCCCGEl6jXV0QTQgghxC/kSFsIIYTwEhLaQgghhJeQ0BZCCCG8hIS2EEII4SUktIUQQggvIaEt\nhBBCeAmj1gXUtVdffZXdu3ej0+lIS0ujU6dOnucWL15MdnY2er2ejh07Mm3aNBwOB9OmTaOwsBCn\n08mkSZOIiYlhxIgRVFRUEBAQAMDkyZPp2LGjVm1d5Hp7TE9P55133qFly5YA9OjRgz/96U/k5+cz\nc+ZMANq1a8esWbO0aOd3rre/Dz/8kC1btgDgcrkoKSlh/fr19O/fn5tvvhmDwQDAnDlziIyM1KSn\nX7tSfxs2bODDDz/EbDYTHx/P8OHDL7vO8ePHmTRpEk6nk/DwcN58803MZrNWbXnUpL833niD7777\nDofDwR//+Efuv/9+pkyZwp49e2jcuDEAqamp9O3bV4uWfud6e9y6dSvPPvssbdu2BeD222/n5Zdf\n9pl9uGzZMrKzsz0/k5eXx86dO+v1++i+ffsYP348o0eP9vwd/mzLli289dZbGAwGevfuzYQJE4A6\neh2qBmTr1q3qySefVEopdeDAATVkyBDPc+fPn1f9+vVTdrtdKaXUmDFj1M6dO9Xy5cvVjBkzlFJK\n7du3Tw0ePFgppdTw4cPV3r1767aBa1CTHlesWKFee+21321r+PDhavfu3UoppZ577jn15Zdf1kEH\nV1aT/n4tPT1dLViwQCmlVL9+/ZTVaq2jyq/NlfpzOp2qd+/e6vTp08rpdKqxY8eq48ePX3adKVOm\nqDVr1iillJo7d65avHhxHXfzezXpLzc3V40bN04ppdSZM2dUnz59lFJKTZ48WW3cuLHOe7iamvT4\n7bffqokTJ/5uW76yD3+7/syZM5VS9fd9tLy8XA0fPly99NJL6h//+Mfvnn/ooYfUsWPHlNPpVMOG\nDVP79++vs9dhgxoez83NJTY2FoCoqCjKysqwWq0AmEwmTCYTFRUVOBwOKisrCQkJISEhgalTpwIQ\nGhrK2bNnNav/WtSkx0uprq7m6NGjnk/Q/fr1Izc3t26auIL/pD+Hw8Fnn332u0/N9cmV+istLSU4\nOJjQ0FD0ej333nsvW7Zsuew6W7duZcCAAYB37L/L9detWzfeeecdAIKDg6msrMTpdGrWw9XUpMfL\n8ZV9+Gvvv/8+48ePr/O6r4fZbGbBggVERET87rmioiJCQkJo2rQper2ePn36kJubW2evwwYV2iUl\nJTRp0sTzODQ0lOLiYgAsFgsTJkwgNjaWfv360blzZ1q3bo3JZMJisQDwySefMGjQIM/68+bN4/HH\nH2f69OlUVVXVbTOXUZMeAbZt20ZqaiqjRo3ihx9+8Lz4fhYWFubZjpZq2h9ATk4O9913H35+fp5l\nM2bMYNiwYcyZMwdVDy4OeKX+QkNDKS8v5/Dhw9jtdrZu3UpJScll16msrPQMw3nD/rtcfwaDwTN8\nunz5cnr37u2Z0li0aBEjR47kL3/5C2fOnKn7hi6hJj0CHDhwgKeeeophw4bxzTffAPjMPvzZ999/\nT9OmTQkPD/csq4/vo0aj8aL3iV8rLi4mNDTU8/jn/uvqddjg5rR/7ddv0larlfnz57Nu3ToCAwMZ\nNWoU+fn5REdHA+650j179vDRRx8BMHLkSNq1a0fLli2ZMWMGixcvJjU1VZM+ruRaeuzcuTOhoaH0\n7duXnTt3MnnyZD7++OPLbqc+uZ59uGLFiovm5Z955hl69epFSEgIEyZMYP369Tz44IN13sOV/Lo/\nnU7Ha6+9RlpaGkFBQTRv3vyq61xpWX1wPf1t2LCB5cuX87e//Q2AxMREGjduTPv27fnrX//Ke++9\nx/Tp0+u0/mtxLT22atWKp59+moceeoiioiJGjhxJTk7OZbdTn1zPPly+fDnJycmex97yPloTtfU6\nbFBH2hERERd96jt16pTnE19BQQEtWrQgNDQUs9lMTEwMeXl5ACxbtoyNGzfywQcfYDKZAIiLi/Oc\nuNW/f3/27dtXx91cWk16jIqK8pzA06VLF86cOUOTJk0umgo4efLkJYeK6lpN92FFRQUnTpy46E0k\nKSmJsLAwjEYjvXv3rhf78Er9Adx99918+umnzJ8/n6CgIJo1a3bZdQICAjxHLt6w/+DS/QH861//\n4qOPPmLBggUEBQUB0L17d9q3bw94z2sQLt1jZGQkAwcORKfT0bJlS2666SZOnjzpU/sQ3MP9Xbp0\n8Tyur++jV/Lb/n/eL3X1OmxQod2zZ0/Wr18PwJ49e4iIiCAwMBCAZs2aUVBQ4PnPzcvLo1WrVhQV\nFbFkyRLee+89zzC5UorRo0dz7tw5wP2H+PNZn1qrSY8LFixg1apVgPuMyZ9Dr02bNuzYsQNwDy33\n6tVLg44uVpP+APLz82nTpo1nO+fPnyc1NZXq6moAtm/fXi/24ZX6Axg3bhynT5+moqKCTZs20b17\n98uu06NHD89yb9h/cOn+zp8/zxtvvMH8+fM9Z4oDTJw4kaKiIsB7XoNw6R6zs7NZuHAh4B5+PX36\nNJGRkT6zD8EdWI0aNfIMFdfn99Erad68OVarlZ9++gmHw8GmTZvo2bNnnb0OG9xdvubMmcOOHTvQ\n6XTMmDGDH374gaCgIOLi4liyZAnp6ekYDAa6dOnCpEmTeOutt1i9ejW33HKLZxsLFy5kw4YNfPzx\nx/j7+xMZGckrr7yCv7+/hp394np7PHHiBC+++CJKKRwOh+erCgcOHGD69Om4XC46d+7sOSFPa9fb\nH8D69evZsmXLRcPjn3zyCZmZmVgsFu644w5efvlldDqdVm15XKm/nJwc3n//fXQ6HWPHjiUhIeGS\n60RHR3Pq1CkmT56MzWbjlltuYfbs2Z6RIi1db39Lly7l3Xffvej8hNdff53CwkLefPNN/P39CQgI\nYPbs2YSFhWnY2S+ut0er1coLL7zAuXPnsNvtPP300/Tp08dn9iG4P0S//fbbF029rVmzpl6+j+bl\n5fH6669z9OhRjEYjkZGR9O/fn+bNmxMXF8f27duZM2cOAPfff79nSL8uXocNLrSFEEIIb9WghseF\nEEIIbyahLYQQQngJCW0hhBDCS0hoCyGEEF5CQlsIIYTwEhLaQgghhJeQ0BZCCCG8hIS2EEII4SX+\nP1stdShFNWmTAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jgmH3wwt1src",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Okay, so we are doing good!
\n",
+ "\n",
+ "Now, let me just put everything here into one function so that you can tweak the hyperparameters easily!\n",
+ "\n",
+ "Or better, do it yourself!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "OZ5TY7B_4E_v",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "def linear_regression(learning_rate=0.000005, n_epochs=100, interval=50):\n",
+ " # YOUR CODE HERE\n",
+ " pass"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "A6MaclhK4rc6",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Okay! Now let's tweak!\n",
+ "linear_regression(learning_rate=0.000034, n_epochs=500)"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "peoHmV2M40uU",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.0000006, n_epochs=1000)"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "KjY_KnlE5ClG",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "## Drive the loss to a minimum."
+ ]
+ },
+ {
+ "metadata": {
+ "id": "JKiHjGN15HPX",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 34
+ },
+ "outputId": "9315862c-c515-42bf-e1ca-74c955bf7f62"
+ },
+ "cell_type": "code",
+ "source": [
+ "# YOUR CODE HERE\n",
+ "tf.reduce_min(loss)"
+ ],
+ "execution_count": 31,
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ },
+ "execution_count": 31
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "C4HRKCeZOaH9",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ ""
+ ],
+ "execution_count": 0,
+ "outputs": []
+ }
+ ]
+}
\ No newline at end of file