diff --git a/First_Date_with_TensorFlow_FT.CyraX.ipynb b/First_Date_with_TensorFlow_FT.CyraX.ipynb
new file mode 100644
index 0000000..822dc5f
--- /dev/null
+++ b/First_Date_with_TensorFlow_FT.CyraX.ipynb
@@ -0,0 +1,1041 @@
+{
+ "nbformat": 4,
+ "nbformat_minor": 0,
+ "metadata": {
+ "colab": {
+ "name": "First_Date_with_TensorFlow.ipynb",
+ "version": "0.3.2",
+ "provenance": [],
+ "include_colab_link": true
+ },
+ "kernelspec": {
+ "name": "python3",
+ "display_name": "Python 3"
+ }
+ },
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "view-in-github",
+ "colab_type": "text"
+ },
+ "source": [
+ " "
+ ]
+ },
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "2XXfXed5YLbe",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# First Date with TensorFlow\n",
+ "\n",
+ "Hi all,
\n",
+ "\n",
+ "You know what's important for understanding Deep Learning / Machine Learning?
\n",
+ "Intuition. Period.\n",
+ "\n",
+ "And Intuition comes when you run the code multiple times.\n",
+ "\n",
+ "So, today I can write a couple of defination and say this is this, this is that.
\n",
+ "You Google half of the things up. You find answers which you need to Google further.
\n",
+ "In the process, you probably won't even remember what's the first thing you started out with!\n",
+ "\n",
+ "So?\n",
+ "\n",
+ "Hence on, I will execute cells with code.
\n",
+ "The neurons in your brain will optimize a function to get a hold of what each function is doing.
\n",
+ "**No Theory Just Code.**\n",
+ "\n",
+ "I will at max give a defination that extends for a line. That's it.
\n",
+ "Let's get started!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "**RECOMMENDED!**
\n",
+ "Write the code in the cells using the signals sent by your brain to your fingers!
\n",
+ "Don't just `shift+enter` the cells.\n",
+ "\n",
+ "[Source](https://github.com/iArunava/TensorFlow-NoteBooks)"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "gYWUpE-bYKWP",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Essential imports\n",
+ "import numpy as np\n",
+ "import tensorflow as tf\n",
+ "import matplotlib.pyplot as plt"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "eKpz5NCIYMdi",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define some tensors\n",
+ "t1 = tf.constant(2.0, dtype=tf.float32)\n",
+ "t2 = tf.constant([1.0, 2.0], dtype=tf.float32)\n",
+ "t3 = tf.constant([[[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]], \n",
+ " [[1.0, 9.0], [2.0, 3.0], [4.0, 5.0]]])"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "vmMcjzTxbWzw",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "f7d8dd1e-4ca8-4473-ef20-1709a6d2c805"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's print them out!\n",
+ "print (t1)\n",
+ "print (t2)\n",
+ "print (t3)"
+ ],
+ "execution_count": 3,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Tensor(\"Const:0\", shape=(), dtype=float32)\n",
+ "Tensor(\"Const_1:0\", shape=(2,), dtype=float32)\n",
+ "Tensor(\"Const_2:0\", shape=(2, 3, 2), dtype=float32)\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "10ahnfjYbcop",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Where's Waldo?
\n",
+ "I mean, the value?
\n",
+ "\n",
+ "So, the thing is you can't print the value of tensors directly.
\n",
+ "You have to use `session`, so let's do that!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "ol6O5I7Tb2nb",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 204
+ },
+ "outputId": "ce13a6aa-e900-4812-c6a2-58e2ef1a2eff"
+ },
+ "cell_type": "code",
+ "source": [
+ "sess = tf.Session()\n",
+ "print (sess.run(t1))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t2))\n",
+ "print (\"=======================\")\n",
+ "print (sess.run(t3))\n",
+ "sess.close()"
+ ],
+ "execution_count": 4,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "2.0\n",
+ "=======================\n",
+ "[1. 2.]\n",
+ "=======================\n",
+ "[[[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]\n",
+ "\n",
+ " [[1. 9.]\n",
+ " [2. 3.]\n",
+ " [4. 5.]]]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "rXKfVs_zb-kU",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Aaahaa!! Just printed those tensors!!!
\n",
+ "Feels good!
\n",
+ "\n",
+ "For some of you, who are like, dude you got \"No Theory Just Code\" in bold
\n",
+ "And you are still using the markdown cells for the theory ?!\n",
+ "\n",
+ "I am just gonna say I am a unreasonable man.
\n",
+ "\n",
+ "\n",
+ "So, you are programming with tf.
\n",
+ "What ever you do is broken down to 2 basic steps:\n",
+ "- Building the computational Graph!\n",
+ "- Execute that graph using `session`!\n",
+ "\n",
+ "That's all!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Let's compare this 2 steps with what we did above!
\n",
+ "So, I defined 3 `tensor`s and these 3 `tensor`s formed my computational Graph.
\n",
+ "And then I executed each tensor in this graph using a `session`.\n",
+ "\n",
+ "That simple!\n",
+ "\n",
+ "
\n",
+ "\n",
+ "Now, let's define a few more computational graphs and execute them with sessions.\n",
+ "\n",
+ "Okay, to start with let's build this computational graph!\n",
+ "\n",
+ "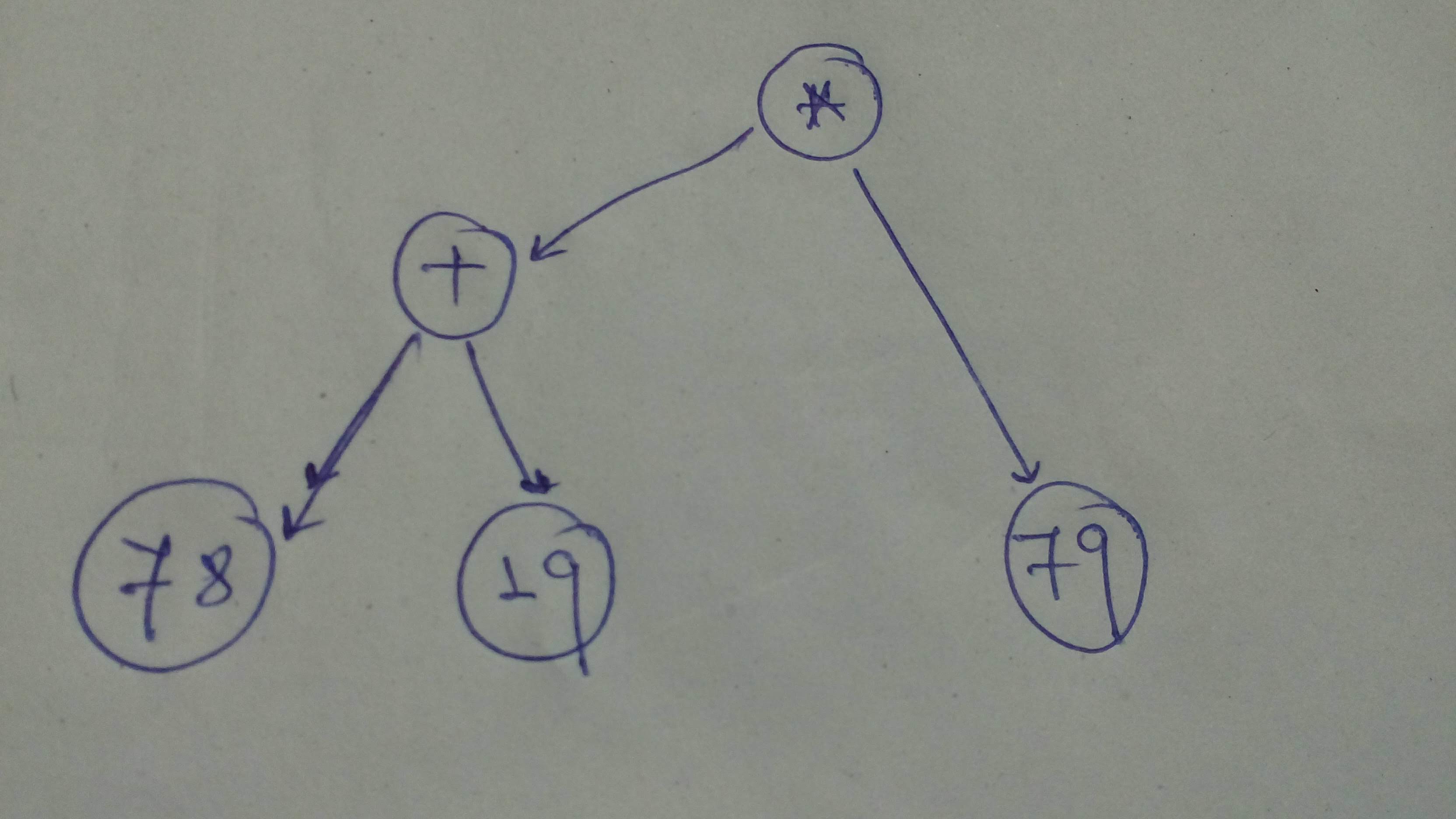"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "FyVz0GNqgreZ",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 51
+ },
+ "outputId": "8e10aa64-9ba0-41e3-c843-c76fb613d1a0"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the graph\n",
+ "comp_graph_1 = tf.multiply(tf.add(78, 19), 79)\n",
+ "\n",
+ "# Alternatively\n",
+ "comp_graph_1_alt = (tf.constant(78) + tf.constant(19)) * tf.constant(79)\n",
+ "\n",
+ "# Let's execute using session\n",
+ "sess = tf.Session()\n",
+ "print ('Comp Graph 1 : ', sess.run(comp_graph_1))\n",
+ "print ('Comp Graph 1 Alt: ', sess.run(comp_graph_1_alt))\n",
+ "sess.close()"
+ ],
+ "execution_count": 5,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Comp Graph 1 : 7663\n",
+ "Comp Graph 1 Alt: 7663\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "SVMMtuFYhaQB",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's define a sligtly more involved graph!\n",
+ "\n",
+ "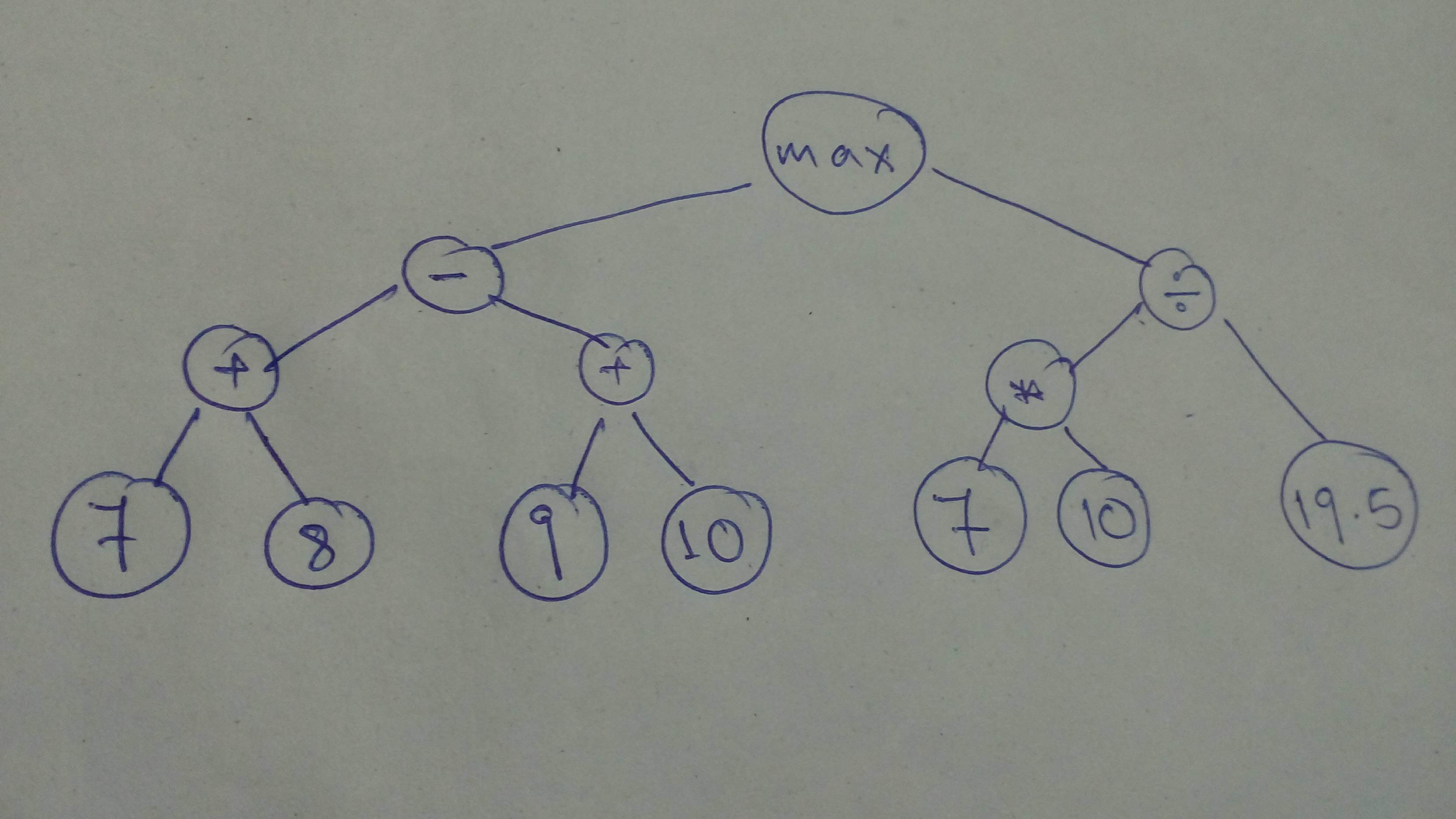"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "4856BTvRhiBb",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "b2fdbb48-417a-4548-cd54-d42a9d2a3bc3"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let build the graph\n",
+ "# We need to cast cause the tensors operated on should be of the same type\n",
+ "comp_graph_part_1 = tf.cast(tf.subtract(tf.add(7, 8), tf.add(9, 10)), \n",
+ " dtype=tf.float32)\n",
+ "comp_graph_part_2 = tf.divide(tf.cast(tf.multiply(7, 10), dtype=tf.float32), tf.constant(19.5))\n",
+ "comp_graph_complete = tf.maximum(comp_graph_part_1, comp_graph_part_2)\n",
+ "\n",
+ "# Let's execute\n",
+ "sess = tf.Session()\n",
+ "part1_res, part2_res, total_res = sess.run([comp_graph_part_1, comp_graph_part_2, comp_graph_complete])\n",
+ "print ('Complete Result: ', total_res)\n",
+ "print ('Part 1 Result: ', part1_res)\n",
+ "print ('Part 2 Result: ', part2_res)\n",
+ "sess.close()"
+ ],
+ "execution_count": 6,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: 3.5897436\n",
+ "Part 1 Result: -4.0\n",
+ "Part 2 Result: 3.5897436\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "B-_ZDtEbj4N0",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Cool! Let's go! Build another graph and execute it with sessions.
\n",
+ "\n",
+ "But this time, it's all you!\n",
+ "\n",
+ "Build this graph and execute it with `session`!\n",
+ "\n",
+ "\n",
+ "\n",
+ "_Remember that `tensors` operated on should be of the same type!_
\n",
+ "_Search up errors and other help you need on Google_"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "-uHNe1BolJY0",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "d2f5e023-cf59-46c2-d83b-86476d8eb5a5"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
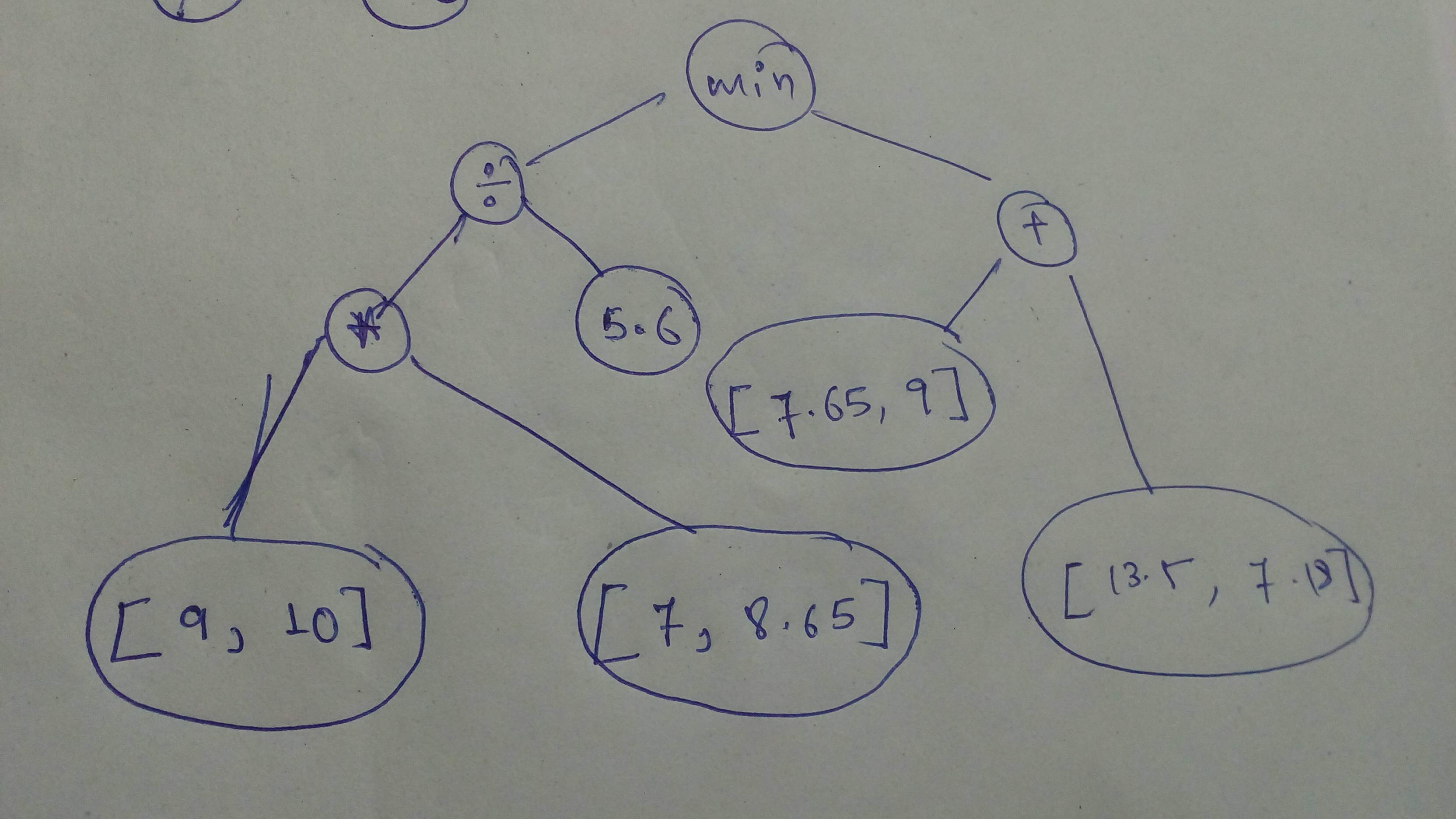
+ "cog1 = tf.divide(tf.cast(tf.multiply([9.0,10.0], [7.0,8.65]), dtype=tf.float32), tf.constant(5.6))\n",
+ "cog2 = tf.cast(tf.add([7.65,9.0], [13.5,7.18]),dtype=tf.float32)\n",
+ "cg = tf.minimum(cog1, cog2)\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "sess = tf.Session()\n",
+ "p1_res, p2_res, total_res = sess.run([cog1, cog2, cg])\n",
+ "print ('Complete Result: ', total_res)\n",
+ "print ('Part 1 Result: ', p1_res)\n",
+ "print ('Part 2 Result: ', p2_res)\n",
+ "sess.close()"
+ ],
+ "execution_count": 7,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: [11.25 15.446429]\n",
+ "Part 1 Result: [11.25 15.446429]\n",
+ "Part 2 Result: [21.15 16.18]\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "qmap38WelREN",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Let's do another!
\n",
+ "It's fun! Isn't it?!\n",
+ "\n",
+ "Build and execute this one!\n",
+ "\n",
+ "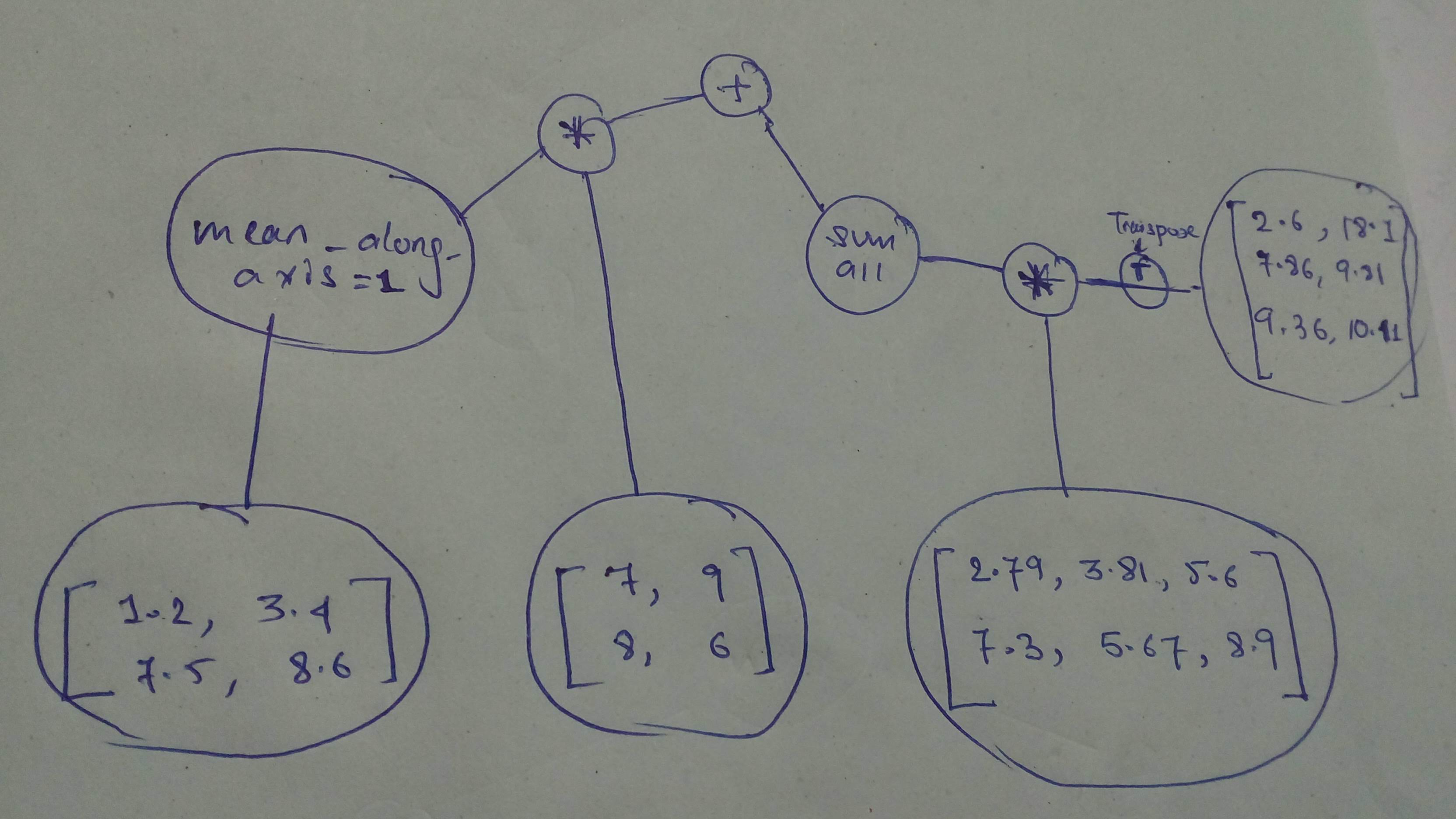"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "0ZhYwAlLmEvB",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 119
+ },
+ "outputId": "a0b734b0-bc89-45eb-c896-1534776a1fd0"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "X=np.array([[1.2,3.4],[7.5,8.6]])\n",
+ "Y=np.array([[7.0,9.0],[8.0,6.0]])\n",
+ "print(np.min(X,axis=1))\n",
+ "kk=tf.cast(tf.multiply(np.min(X,axis=1),Y),dtype=tf.float32)\n",
+ "sess=tf.Session()\n",
+ "Z=np.array([[2.6,18.1],[7.86,9.81],[9.36,10.41]])\n",
+ "Z=np.transpose(Z)\n",
+ "W=np.array([[2.79,3.81,5.6],[7.3,5.67,8.9]])\n",
+ "kk2=tf.cast(np.sum(sess.run(tf.multiply(W,Z))),dtype=tf.float32)\n",
+ "f=tf.add(kk,kk2)\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "p1_res, p2_res, total_res = sess.run([kk, kk2, f])\n",
+ "print ('Complete Result: ', total_res)\n",
+ "print ('Part 1 Result: ', p1_res)\n",
+ "print ('Part 2 Result: ', p2_res)\n",
+ "sess.close()"
+ ],
+ "execution_count": 9,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "[1.2 7.5]\n",
+ "Complete Result: [[378.4183 437.5183 ]\n",
+ " [379.61832 415.0183 ]]\n",
+ "Part 1 Result: [[ 8.4 67.5]\n",
+ " [ 9.6 45. ]]\n",
+ "Part 2 Result: 370.0183\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "BnB0b6qCmGmg",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "And a final one, before we move on to the next part!\n",
+ "\n",
+ "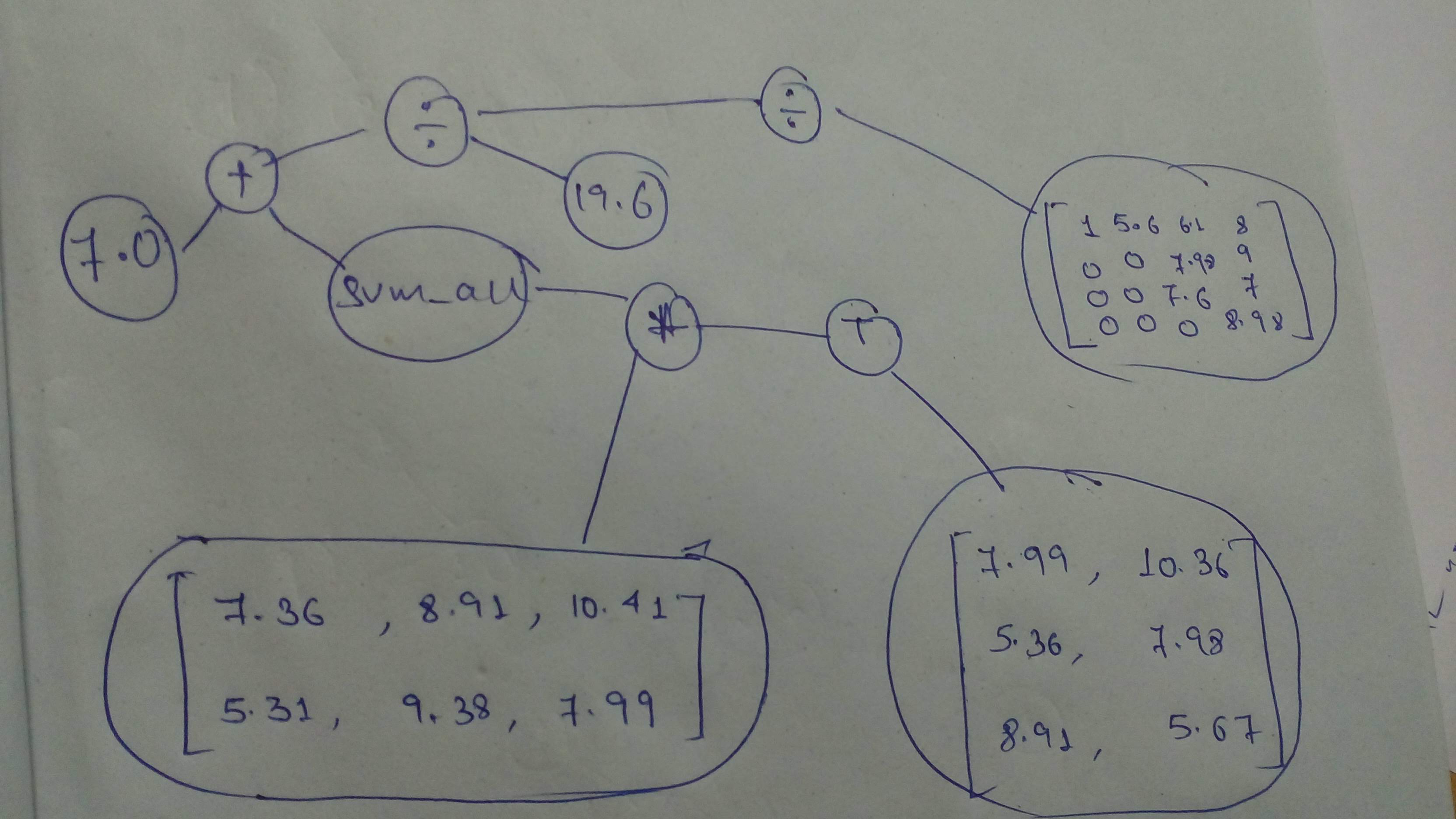"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "GQWyCvsQmMcL",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 68
+ },
+ "outputId": "1681058a-f49c-4d11-ea0b-a4b354ae17af"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Build the graph\n",
+ "# YOUR CODE HERE\n",
+ "sess=tf.Session()\n",
+ "X=np.array([[7.36,8.91,10.41],[5.31,9.38,7.99]])\n",
+ "Y=np.transpose(np.array([[7.99,10.36],[5.36,7.98],[8.91,5.67]]))\n",
+ "kk=tf.cast(tf.divide(tf.add(7.0,np.sum(sess.run(tf.multiply(X,Y)))),19.6),dtype=tf.float32)\n",
+ "ttl=tf.divide(kk,tf.constant([[1,5.6,6.1,8],[0,0,7.98,9],[0,0,7.6,7],[0,0,0,8.98]],dtype=tf.float32))\n",
+ "# Execute \n",
+ "# YOUR CODE HERE\n",
+ "xRes,ttlRes = sess.run([kk, f])\n",
+ "print ('Complete Result: ', ttlRes)\n",
+ "print ('Part 1 Result: ', xRes)\n",
+ "\n",
+ "sess.close()"
+ ],
+ "execution_count": 11,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Complete Result: [[378.4183 437.5183 ]\n",
+ " [379.61832 415.0183 ]]\n",
+ "Part 1 Result: 19.46349\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "12NC7XTPsJw7",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "# Linear Regression\n",
+ "\n",
+ "Okay, now we will create a dummy dataset and perform linear regression on this dataset!\n",
+ "\n",
+ "\n",
+ "To get you in the habit of looking up for the documentation, I am not providing what some of the following functions does, Google them up!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "hW31RZkjtNwI",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Create the dataset\n",
+ "X = np.linspace(-30.0, 300.0, 300)\n",
+ "Y = 2 * np.linspace(-30.0, 250.0, 300) + np.random.randn(*X.shape)\n",
+ "\n",
+ "# Normalize the dataset\n",
+ "X = X / np.max(X)\n",
+ "Y = Y / np.max(Y)\n",
+ "\n",
+ "# Divide it into train and test\n",
+ "train_X = X[:250]\n",
+ "train_Y = Y[:250]\n",
+ "\n",
+ "test_X = X[250:]\n",
+ "test_Y = Y[250:]"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "LQKy6U33y4lt",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the hyperparameters\n",
+ "learning_rate = 0.00001\n",
+ "n_epochs = 60\n",
+ "interval = 20"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "1h1-D8K1uT48",
+ "colab_type": "code",
+ "outputId": "90416653-4148-429f-fbb1-502a71289b31",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 350
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# let's viz the first 10 datapoints of the dataset\n",
+ "plt.plot(train_X[:10], train_Y[:10], 'g')\n",
+ "plt.show()"
+ ],
+ "execution_count": 14,
+ "outputs": [
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAfIAAAFNCAYAAAD7De1wAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3XtcVHX+x/HXcAcFBAO09VKWl8ww\nryh4SctSanfbTUwqjLKLaXbRdkU00dTAEjN+VptlZmZaVGutGVlGbCZpSpFZamWmaeFgXESQQTi/\nP0x2WVN0HDjMzPv5ePSAOXPOmc+nA7453/OdMxbDMAxERETEKXmYXYCIiIjYT0EuIiLixBTkIiIi\nTkxBLiIi4sQU5CIiIk5MQS4iIuLEvOzZqKqqiqSkJA4cOICnpyepqam0bdu2zjpvv/02y5Ytw8PD\ng1GjRhEXF0dBQQHJycnYbDZqamqYOnUq3bp1Y+jQobRq1QpPT08A5s+fT0RExLl3JyIi4uLsCvI1\na9YQFBREeno6GzZsID09nYULF9Y+X15ezlNPPcXrr7+Ot7c3I0eOZNiwYbz44osMGzaM0aNHk5eX\nxxNPPMGSJUsAeO6552jWrJljuhIREXETdg2t5+bmMmzYMACio6PJy8ur83x+fj6XXXYZgYGB+Pn5\n0bNnT/Ly8ggJCaG4uBiA0tJSQkJCzrF8ERER92bXGXlhYSGhoaEAeHh4YLFYsNls+Pj4nPQ8QGho\nKFarlcTEREaOHMnq1aspKytj5cqVteukpKSwf/9+evXqxeTJk7FYLKd8/WPHqvHy8rSndBEREZdS\nb5BnZmaSmZlZZ1l+fn6dx/Xd5fXE888//zwjRozgnnvuITs7m3nz5rFo0SLuu+8+Bg4cSHBwMBMm\nTOC9995j+PDhp9xfUVF5fWWftbCwQKzWww7fb1Omnt2DO/YM7tm3enZtYWGBv7u83qH1uLg4Xnvt\ntTr//eUvf8FqtQLHJ74ZhlF7Ng4QHh5OYWFh7eODBw8SHh5OXl4eAwcOBCAmJoavvvoKgOuvv56W\nLVvi5eXFoEGD2LVrl/2dioiIuBG7rpHHxMSQlZUFQHZ2NlFRUXWe7969O9u2baO0tJQjR46Ql5dH\n7969ad++fe3Z/Jdffkn79u05fPgwY8eOxWazAfDZZ5/RsWPHc+lJRETEbdh1jTw2NpaNGzcSHx+P\nj48PaWlpACxevJg+ffrQo0cPJk+ezNixY7FYLEyYMIHAwEDuvvtupk2bVvtHwLRp0wgMDGTQoEHc\neOON+Pr60rVr19MOq4uIiMh/WJzxY0wb4nqIO11nOUE9uwd37Bncs2/17NrsvkYuIiIiTZeCXERE\nxIkpyEVERJyYglxERMSJKchFREScmIJcRETEiSnIRUREHOhA2X5e27mSquqqRnk9u24IIyIiInUd\nqTrCU58/yVNfPEnFsQo6hXTm8vCeDf66CnIREZFzUGPU8PquV5n76Sx+PnKA8IAI5g1a0CghDgpy\nERERu23+eRMPfzKFzw/m4evpy4O9HmJijwdp7vP7d2FrCApyERGRs7Tv8F5m585g9XdvAnD9xX/l\n4f6P0DawXaPXoiAXERE5Q2VVZfxf3gKe/uL/qKyupEd4Tx6JSSOqdT/TalKQi4iI1KPGqOHVHa8w\nd9MsDpYX0KpZa6b3m8nITjfiYTH3DWAKchERkdPIPfAJD38ylS+tX+Dv5c9DvZOY0ON+mnk3M7s0\nQEEuIiLyu/aU/MAjuTNYs/stAG7oOIrp/Wbyh8A2JldWl4JcRETkvxy2lbJwazrP5j+FrcZGr4g+\nzBmQRq+IPmaX9rsU5CIiIkB1TTWv7FhO6qbZFFZY+UPzNjzcfxZ/uXgkFovF7PJOSUEuIiJu7+Of\ncnj4k6l8fegrArwCSOo7nXHd7yXAO8Ds0uqlIBcREbe1u/g7ZuY+TNYP7wBwY+ebmNYvhVbNWptc\n2ZlTkIuIiNspqSxmwZbHeX7bP6iqqSKqdX9mx6Q22m1VHUlBLiIibuNYzTGWf/0ij22ey6Gjh2gb\n2I6U/rP540XXN+nr4KejIBcREbeQvXc9KRuT2fHrNzTzbs70fjO5K3I8fl5+Zpd2ThTkIiLi0r4r\n+paUjcm8/+N7WLBw8yVjSIp6mIiACLNLcwgFuYiIuKSio7+SvmUeL3z1HMdqjhFz/kAeGZDKZedF\nml2aQynIRUTEpVRVV7Fs+xIe/yyVosoiLgi6kJnRcxlx4bVOex38dBTkIiLiMtb/uI4ZnyTzbfEu\nAn2CSOk/hzsi78bX09fs0hqMglxERJzezl93kLIxmQ/3foCHxYMxXW9nSt9phAWEmV1ag1OQi4iI\n0yosLyTp38ks2/4C1UY1g9oM4ZGYR+na8lKzS2s0CnIREXE6tmobL3y1mAVbH6P4aDEdgi/ikZhH\nGdZ+uEteBz8dBbmIiDgNwzBY92MWKZ8ks7vke1r4tWB2TCq3dbsTH08fs8szhYJcREScwteHtjPj\nk2T+/VM2nhZPbu92J/NGPIpxxHUnsp0Ju4K8qqqKpKQkDhw4gKenJ6mpqbRt27bOOm+//TbLli3D\nw8ODUaNGERcXR3l5OUlJSRQWFuLv709aWhphYWHs2LGDmTNnAtC5c2dmzZp1zo2JiIhrsJZbmbd5\nLi9/8yI1Rg1D213FrOhH6RzahfMCArEeOWx2iaayK8jXrFlDUFAQ6enpbNiwgfT0dBYuXFj7fHl5\nOU899RSvv/463t7ejBw5kmHDhrF69Wratm1LRkYGW7ZsISMjg9mzZzN37lySk5OJjIxk8uTJ5OTk\nMHjwYIc1KSIiTYOt2kaprZRSWwmllSWUVJYcf/zb1xJbce33pZUllNhK+KpwG4dtpXQK6cys6Llc\n2f5qs9toUuwK8tzcXK6//noAoqOjSU5OrvN8fn4+l112GYGBgQD07NmTvLw89uzZQ//+/QHo3bs3\nM2bMwGazsX//fiIjj99pZ8iQIeTm5irIRUSaGMMwKD9WXhuwpZWllNqKjwdwZcl/wriyhMO24+sc\n//63520lVByrOOvXbdWsNclRDzOm6+14e3o3QGfOza4gLywsJDQ0FAAPDw8sFgs2mw0fH5+TngcI\nDQ3FarXSqVMncnJyuOaaa9i8eTMHDhygqKiIoKCg2nVbtmyJ1Wo9l55EROQUSiqLKa4srhO6tWfH\ntv86Ez4RwLYTAX18WbVRfVav5+XhRbBPMEG+wbRu1ppA3+Djj32CCPINJtj3t+9/W+fEukE+QQT7\nBtPcOxBPD88G+r/hGuoN8szMTDIzM+ssy8/Pr/PYMIzT7uPE8yNHjmTnzp3Ex8fTt2/fOmF/pvsC\nCAkJwMvL8Qc2LCzQ4fts6tSze3DHnsE9+z5Vz2W2MhJXJ/LGN2+c1f6aeTejhV8LWgW2oktYF1r4\ntSDYN7jO1xZ+LQj2+/1l/l7+Df52MHc8zv+t3iCPi4sjLi6uzrKkpCSsVitdunShqqoKwzBqz8YB\nwsPDKSwsrH188OBBLr/8cnx8fGonsh05coT169cTGhpKcXFx7boFBQWEh4eftqaiovIz6+4shIUF\nYrW614QJ9ewe3LFncM++T9XzT4f3kbB2NNsPbeOy87rTteWlv50JBxPkG0SwTwsCfzsDDvYNrv0+\n0DvI/qHso3DkaDVHKDvHrk7PnY7zqf5gsWtoPSYmhqysLAYOHEh2djZRUVF1nu/evTvTp0+ntLQU\nT09P8vLySE5OJicnh88//5wHHniAt99+m4EDB+Lt7U2HDh3YsmULvXv3Zt26dSQkJNhTloiI/I8t\nv2zm1ndvwlpxkDFdbyd14OO6zuxi7Ary2NhYNm7cSHx8PD4+PqSlpQGwePFi+vTpQ48ePZg8eTJj\nx47FYrEwYcIEAgMDiYqKYsWKFYwaNYrg4GAWLFgAQHJyMjNmzKCmpobu3bsTHR3tuA5FRNzUG7te\n44HsCVTVVPHogMcYe9ndbnfXM3dgMc7konQT0xDDKO40PHOCenYP7tgzuGffJ3quMWqYt3kOT2yd\nT6BPEM9d/SJD211ldnkNwp2Os0OH1kVEpGk6UnWEe9ffzTu73+aCoAt5OfY1OoV2NrssaUAKchER\nF/FT6U/86Z/Xsa0wn+jzB/DC8OWE+rU0uyxpYB5mFyAiIucur2ALfZ7rw7bCfBK6JvLaH1crxN2E\nzshFRJzcP799nfs/HI+txsbsmFTuihyvSW1uREEuIuKkaowaHv8slfQt82juHcibN75J7xYDzC5L\nGpmCXETECZVXlTPxw3H86/vVtAu6gJdjX2Vgx75uM4Nb/kNBLiLiZH4uO8CYd+PJt35Ov9bRLB2+\ngpb+uh7urhTkIiJO5IuDeSSsHU1B+S/c1CWBxwY/gY+nT/0bistSkIuIOIm3vnuTievHUVldyazo\nRxnXfYImtYmCXESkqTMMg/lb0nj8s1SaeTdn+TXLuPqCEWaXJU2EglxEpAmrOFbB/R/ew+rv3qRd\nYHuWx77KJS27ml2WNCEKchGRJuqXIz9z67vxfH4wj76t+rF0+ArCAsLMLkuaGAW5iEgT9KX1CxLW\njubnIwcY3eVmHh+8EF9PX7PLkiZIQS4i0sT86/u3uHf9XRw9dpQZ/Wcz4fL7NKlNTklBLiLSRBiG\nwRNbHydt8xyaeTdn2YiVDL8w1uyypIlTkIuINAEVxyp4MPte3vw2kzbN27I89lUuPa+b2WWJE1CQ\ni4iYrKC8gMR349lasIU+raJYOnwF4QHhZpclTkJBLiJiom2FXzJm7Wj2l/1EXKfRpF+RgZ+Xn9ll\niRNRkIuImGTt7jWM/+AOKo5VML3fTCb2eFCT2uSsKchFRBqZYRhk5C1g7qZZBHgFsHT4CmI7XGd2\nWeKkFOQiIo3o6LGjTPpoIq/vepU/NG/DS7GruOy8SLPLEiemIBcRaSQHyw+S+O5NbCnYTK+I3rw4\nYiURARFmlyVOTkEuItIIthd+RcLaG/mpbB83dBzFE0MWaVKbOISCXESkgWX9sJZx74+l/NgRkqNm\ncH/PyZrUJg6jIBcRaSCGYbDoiyeZk5uCv5c/L1zzMtdd9CezyxIXoyAXEWkAldWVPPTR/by68xVa\nNzuf5bGriAy73OyyxAUpyEVEHKywopDEd29i8y+f0jO8F8tGrCSiWSuzyxIXpSAXEXGgbw59TcLa\nG9l7+Ef+cvENLBz6NP5e/maXJS5MQS4i4iDr9rzL3e+P5UhVGVP6TmNSr79rUps0OAW5iMg5MgyD\nZ/IXMWvjdPy8/Hj+6mX86eK/mF2WuAkFuYjIObBV2/hbzgOs3PEyrZq1ZvmIVXQP72F2WeJG7Ary\nqqoqkpKSOHDgAJ6enqSmptK2bds667z99tssW7YMDw8PRo0aRVxcHOXl5SQlJVFYWIi/vz9paWmE\nhYWRkJBAeXk5AQEBAEyZMoVu3fQ5vCLStB2qOMRtWTfz6c8buTysBy/FrqJVs9ZmlyVuxq4gX7Nm\nDUFBQaSnp7NhwwbS09NZuHBh7fPl5eU89dRTvP7663h7ezNy5EiGDRvG6tWradu2LRkZGWzZsoWM\njAxmz54NQGpqKp06dXJMVyIiDWznrzu4ee0o9pbu4c8X/ZUnhz5NgHeA2WWJG/KwZ6Pc3FyGDRsG\nQHR0NHl5eXWez8/P57LLLiMwMBA/Pz969uxJXl4ee/bsITLy+IcD9O7dm61bt55j+SIijW/j/g1c\n++Yw9pbu4aHeSSy+eqlCXExjV5AXFhYSGhp6fAceHlgsFmw22+8+DxAaGorVaqVTp07k5OQAsHnz\nZg4cOFC7TkZGBjfffDMzZszg6NGjdjUjItLQVn/7BqP+dT0Vx8p5+qrn+HvfZM1MF1PVO7SemZlJ\nZmZmnWX5+fl1HhuGcdp9nHh+5MiR7Ny5k/j4ePr27Vsb9mPGjKFz5860a9eOlJQUVqxYwdixY0+5\nv5CQALy8POsr/ayFhQU6fJ9NnXp2D+7YMzi+7wW5C5j8/mSCfIP4543/ZOiFQx26f0dwx2Ptjj3/\nt3qDPC4ujri4uDrLkpKSsFqtdOnShaqqKgzDwMfHp/b58PBwCgsLax8fPHiQyy+/HB8fH2bNmgXA\nkSNHWL9+PUDtMD3A0KFDWbt27WlrKioqP4PWzk5YWCBW62GH77cpU8/uwR17Bsf2XWPUkPJJMs9+\n+TStm53PK9e+zqXNuzW5/6/ueKzdqedT/cFi19B6TEwMWVlZAGRnZxMVFVXn+e7du7Nt2zZKS0s5\ncuQIeXl59O7dm5ycnNpJcW+//TYDBw7EMAwSExMpLS0FYNOmTXTs2NGeskREHO7osaPcuS6RZ798\nmi6hl7D2rx9w6Xl6V400HXbNWo+NjWXjxo3Ex8fj4+NDWloaAIsXL6ZPnz706NGDyZMnM3bsWCwW\nCxMmTCAwMJCoqChWrFjBqFGjCA4OZsGCBVgsFkaNGkViYiL+/v5EREQwceJEhzYpImKPoqO/cuu7\nN/HpzxuJPn8Ay0a8QrBvC7PLEqnDYtR3gbsJaohhFHcanjlBPbsHd+wZzr3vfYf3Er/mBnYV7eTP\nF/2VRVc9i6+nrwMrdDx3PNbu1LNDh9ZFRFzZtsIviX3jKnYV7WRc93t59uoXmnyIi/vSLVpFRP7L\nR/s+5PasBI5UlTE7JpW7u08wuySR01KQi4j85rWdK3kgewKeFk+eu/pFffCJOAUFuYi4PcMwyMhb\nwNxNswj2bcHyEavod3602WWJnBEFuYi4teqaaqZ+/BAvbl9Cm+ZtWXndG3QO7WJ2WSJnTEEuIm6r\nvKqcce/fTtaetVza8jJWXve6Pr1MnI6CXETcUmFFIQlrR7G1YAuD2gxh6fDlBPoEmV2WyFlTkIuI\n2/mhZDej1/yVH0p2E9dpNE8MWYSPp0/9G4o0QXofuYi4lc8LtnLtm1fxQ8lu7u85mUVXPqsQF6em\nM3IRcRvv78niznWJHK0+yrxBC7it2x1mlyRyzhTkIuIWXv56GX/LeQAfTx+WDl/BiAuvNbskEYdQ\nkIuISzMMg8c+e5T0LfMI9Qvl5djX6N2qr9lliTiMglxEXFZVdRUP5dzPyh0v0y7oAl697g0uaqGP\nSRbXoiAXEZdUZisj4d0b+XDvB1we1oOXr80kPCDc7LJEHE6z1kXE5RSUFzD4xcF8uPcDrmp3NW9e\n/45CXFyWzshFxKV8V/Qto9f8lb2Hf+TmS8bw+OCFeHnonzpxXfrpFhGXsfnnTSSsHUVRZREzB8/k\nnq4PYrFYzC5LpEFpaF1EXMI7u//FyLf/SKmtlIVDniLlihSFuLgFBbmIOL0l2xZze9YteFg8eTn2\nVW66JMHskkQajYbWRcRp1Rg1zP10Fv/3+ROc5x/GK9dmcnl4T7PLEmlUCnIRcUq2ahv3fzieN759\njQ7BF7Hquje5IPhCs8sSaXQKchFxOqWVJdyWdQsf78+hV0QfXo59jZb+Lc0uS8QUCnIRcSo/lx0g\n/p2RfH3oK4ZfeC3/uGoJAd4BZpclYhpNdhMRp7Hj128Y8caVfH3oKxIvHcvSa15WiIvb0xm5iDiF\njfs3MObdeEptJUzvN5OJPfQecRFQkIuIE1j97Rvcu/5uaqhh0ZXPMqpzvNkliTQZGloXkSbtmS8W\ncdf7t+Hj6cvKa99QiIv8D52Ri0iTVGPUkPJJMs9++TQRAa145brXuey8SLPLEmlyFOQi0uQcPXaU\nCevv4l/fr6ZTSGdWXfcmbQLbml2WSJOkIBeRJqXo6K/c+u5NfPrzRvq1jualEStp4RdidlkiTZaC\nXESajH2H9xK/5gZ2Fe3kTxf9hUVXPoufl5/ZZYk0aXYFeVVVFUlJSRw4cABPT09SU1Np27busFdJ\nSQmTJk2iWbNmZGRknHa7HTt2MHPmTAA6d+7MrFmzzq0rEXE62wq/5KY1Iyko/4W7I8czK+ZRPCya\njytSH7t+S9asWUNQUBArV65k3LhxpKenn7ROSkoKvXr1OqPt5s6dS3JyMqtWraKsrIycnBx7yhIR\nJ7X+x3X8+Z8jKCj/hUdiHmX2gDSFuMgZsus3JTc3l2HDhgEQHR1NXl7eSevMmTPnpCD/ve1sNhv7\n9+8nMvL4bNQhQ4aQm5trT1ki4mQKKwq5d/3dxL8zElt1Jc9d/SLjut9rdlkiTsWuofXCwkJCQ0MB\n8PDwwGKxYLPZ8PHxqV2nefPmZ7RdYWEhQUFBteu0bNkSq9VqT1ki4iQMw+DVna8wc+M0fj36K5Fh\nl5M++Em6h/cwuzQRp1NvkGdmZpKZmVlnWX5+fp3HhmHY9eK/t92Z7CskJAAvL0+7XvN0wsICHb7P\npk49u4em1PPOwp3c/c7d5PyYQzPvZjxxzRPc2/devDwcP/e2KfXdWNSz+6n3NycuLo64uLg6y5KS\nkrBarXTp0oWqqioMw6hzNn4q4eHhJ20XFhZGcXFx7ToFBQWEh4efdj9FReX1vtbZCgsLxGo97PD9\nNmXq2T00lZ4rqyt5cms6GXkLsNXYuOaCEaQOnE+bwLYUHapw+Os1lb4bk3p2baf6g8Wua+QxMTFk\nZWUBkJ2dTVRUlN3beXt706FDB7Zs2QLAunXrGDhwoD1liUgT9cn+j7ni1f7M35JGS//zWDp8BS+N\nWKWbvIg4gF1jWbGxsWzcuJH4+Hh8fHxIS0sDYPHixfTp04fIyEgSExMpLS2loKCAhIQExo8ff8rt\nkpOTmTFjBjU1NXTv3p3o6GjHdSgipjlUcYhZudNZtWMFFizcedk4kqKmE+gTVP/GInJGLIa9F7hN\n1BDDKO40PHOCenYPZvRsGAav7VxJysZkfj36K93OiyR98JP0iOhV/8YOomPtHtyp51MNrevObiLi\nUN8Xf8vfcybx8f4cArwCmBX9KHdGjmuQyWwioiAXEQeprK5k0ecLWbh1PpXVlVzdfjipg+bTNrCd\n2aWJuDQFuYics9wDn/DQR/fzbfEuIgJa8ejAx7muw5+wWCxmlybi8hTkImK3oqO/8kjuDFZ88xIW\nLNze7U6So2YQ5BtsdmkibkNBLiJnzTAMXt/1KikbkymsKKRry26kX/EkvSL6mF2aiNtRkIvIWdld\n/B1/+/ckPv7pI/y9/JnRfzZ3R47H29Pb7NJE3JKCXETOiK3axlOfP8mCrY9RWV3Jle2GMW/QAtoF\ntTe7NBG3piAXkXp9+nMuD310H7uKdhIeEMGjAx7jjxddr8lsIk2AglxETqno6K/Mzk3h5W+WYcFC\n4qVjmdYvhWDfFmaXJiK/UZCLyEkMw+DNbzN5+JOpFFZYuST0UuZfsZA+rc7scxVEpPEoyEWkjh9K\ndvP3nAfJ+Skbfy9/pvebxT3d79VkNpEmSkEuIsDxyWzPfPF/pG+Zx9HqowxpeyXzBi3gguALzS5N\nRE5DQS4ibPr5U/6Wcz87fv2GMP9wMgY8w58v/qsms4k4AQW5iBsrPlrE7E9nsvzrpQCM6Xo7D/ef\nqclsIk5EQS7ihgzDYPV3bzB9QxLWioN0Cb2E+YMz6Ntak9lEnI2CXMTN7Cn5gSn/nkT2vvX4efox\nvd9MxnW/Fx9PH7NLExE7KMhF3ERVdRXP5C8ifUsaFccquKLtUOYNWsCFwR3MLk1EzoGCXMQNfPbL\nJh766AG++XU75/mH8cSQRfzl4pGazCbiAhTkIi6spLKYlHem8I8t/8DAIKFrIg/3m0ULvxCzSxMR\nB1GQi7ggwzB4+/t/Mm3DFA6WF9A5pAuPX/Ek/Vr3N7s0EXEwBbmIi9lb+iNJ/57MB3vX4evpy9yh\nc7m1492azCbiohTkIi7kh5LdXPvmVRRWFDKozRAeG7yAqIsvx2o9bHZpItJAFOQiLuLXo4eIX3MD\nhRWFzI5J5a7I8ZrMJuIGFOQiLuDosaOMWRvP7pLvmdjjQe7uPsHskkSkkXiYXYCInJsao4aJ68ex\n+ZdP+cvFNzCtX4rZJYlII1KQizi5OZ/O5K3v3ySqdX+eHPoMHhb9Wou4E/3GizixF79awqLPF3JR\ni4tZNuIV/Lz8zC5JRBqZglzESb2/J4ukjydznv95rLz2DUL9WppdkoiYQEEu4oTyD37Onetuw9fT\nl+Wxr3JB8IVmlyQiJtGsdREns+/wXm5eO4qKY+UsHb6CXhF9zC5JREykIBdxIiWVxdy0ZiQHywuY\nE5NGbIfrzC5JRExmV5BXVVWRlJTEgQMH8PT0JDU1lbZt29ZZp6SkhEmTJtGsWTMyMjJOu11CQgLl\n5eUEBAQAMGXKFLp163aOrYm4Flu1jduybmFn0Q7uiryHu7qPN7skEWkC7LpGvmbNGoKCgli5ciXj\nxo0jPT39pHVSUlLo1avXGW+XmprK8uXLWb58uUJc5H8YhsGD2feyYf+/ib3wj8yKftTskkSkibAr\nyHNzcxk2bBgA0dHR5OXlnbTOnDlzTgryM9lORE722GePkrlrFb0ievP0Vc/h6eFpdkki0kTYNbRe\nWFhIaGgoAB4eHlgsFmw2Gz4+//l0pebNm5/xdgAZGRkUFRVx0UUXkZycjJ+f3g8rArDym5dJ3zKP\n9kEX8NKIVwnwDjC7JBFpQuoN8szMTDIzM+ssy8/Pr/PYMAy7XvzEdmPGjKFz5860a9eOlJQUVqxY\nwdixY0+5XUhIAF5ejj8jCQsLdPg+mzr13LR9sPsDJufcR6h/KO8lZNH5vA527ceZenYkd+xbPbuf\neoM8Li6OuLi4OsuSkpKwWq106dKFqqoqDMOoczZ+KuHh4b+73YnhdoChQ4eydu3a0+6nqKi83tc6\nW2FhgW73UY/quWn7+tB2/vrPG/DAgxeveYVQ43y7anemnh3JHftWz67tVH+w2HWNPCYmhqysLACy\ns7OJioqyezvDMEhMTKS0tBSATZs20bFjR3vKEnEZP5cd4KY1IzlsK2XRlc/S7/xos0sSkSbKrmvk\nsbGxbNy4kfj4eHx8fEhLSwNg8eLF9OnTh8jIyNpwLigoICEhgfHjx//udhaLhVGjRpGYmIi/vz8R\nERFMnDjRoU2KOJMy22FueieOA0f2M73fLK7veIPZJYlIE2Yx7L3AbaKGGEZxp+GZE9Rz01NVXUXC\nuzfy4d4PGNP1dh4f/AQWi+Wc9tnUe24o7ti3enZtDh1aFxHHMwyDpI8n8+HeD7iq3dWkDZp/ziEu\nIq5PQS7SRGTkLWD51y9y2XkGWs5aAAAbdklEQVTdWXzNi3h56A7KIlI/BblIE/DGrteYu2kWf2je\nhhXXvkZz75PvwyAi8nsU5CImyz3wCfd/OJ5AnyBeufZ1WjVrbXZJIuJEFOQiJvq2aBe3vhtPDTUs\nHf4yl7TsanZJIuJkdBFOxCQHyw8Sv+YGiiuLyRj6DIPaXGF2SSLihHRGLmKCI1VHSFg7ir2Hf+Rv\nfaYyusvNZpckIk5KQS7SyKprqrnn/bF8fjCP0V1u5qHeSWaXJCJOTEEu0ogMw+DhT5LI2rOWgW2u\nYP7gJ/VecRE5JwpykUb07JdP8fy2Z7kktCtLr1mOj2f9HzYkInI6CnKRRvKv798i5ZNpRAS04pVr\nXyfIN9jskkTEBSjIRRrBZ79sYsIHdxLg3YxXrs3kD4FtzC5JRFyE3n4m0sB2l3zPmLWjqaqpYunw\nl7ksrLvZJYmIC1GQizSgQxWHuGnNSA4dPcT8wU9yZfurzS5JRFyMhtZFGsjRY0e59d14dpd8z309\nJjHm0tvMLklEXJCCXKQB1Bg13Lv+bjb/8il/ufgGkvvNMLskEXFRCnKRBjA7N4W3v/8n/VpHk3Hl\nP/Cw6FdNRBqG/nURcbClXz3PU188ycUtOrJsxCv4evqaXZKIuDAFuYgDrdvzLlM/fojz/M/jlWtf\nJ8Qv1OySRMTFKchFHCT/4Ofcte42fD19eTn2NS4IvtDskkTEDejtZyIOsO/wXm5eO4qKYxW8OOIV\nekb0NrskEXETCnKRc1RSWcxNa0ZysLyAuQPmMeLCa80uSUTciIbWRc6BrdrGbVm3sLNoB3dHjufO\nyHvMLklE3IyCXMROhmHwYPa9bNj/b2Iv/CMzo+eaXZKIuCEFuYid5n02l8xdq+gV0Zunr3oOTw9P\ns0sSETekIBexwyvfLGfBlsdoH3QBL414lQDvALNLEhE3pSAXOUsf7fuQh3LuJ8Q3hFXXvUFYQJjZ\nJYmIG1OQi5yF7YVfcXtWAp4WT5bFruKiFh3NLklE3JzefiZyhn4uO8BN74ykrOowi4ctpV/r/maX\nJCKiM3KRM3HYVspN78Tx85EDPNz/Ea7veIPZJYmIAApykXpVVVdxx3u3sv3QNm69dCz3Xn6/2SWJ\niNSyK8irqqqYPHky8fHx3HLLLezbt++kdUpKShg7diz33XdfneWbN2+mf//+ZGdn1y7bsWMHo0eP\nZvTo0aSkpNhTkkiDMAyDKf+eRPa+9Qxrfw2pAx/HYrGYXZaISC27gnzNmjUEBQWxcuVKxo0bR3p6\n+knrpKSk0KtXrzrL9u7dy9KlS+nZs2ed5XPnziU5OZlVq1ZRVlZGTk6OPWWJnBPDMCipLOa7om/Z\nuH8Db333JkkfT+blb5YRGXY5z169FC8PTSsRkabFrn+VcnNzuf766wGIjo4mOTn5pHXmzJnD9u3b\n2bFjR+2ysLAwFi1axLRp02qX2Ww29u/fT2RkJABDhgwhNzeXwYMH21OaSB2GYXCkqoyD5QUcrLBS\naS3lu19+xFpegLXCysHyAqzlBzlYfhBrxUEqqytP2keb5m1ZEfsazb2bm9CBiMjp2RXkhYWFhIYe\n/5xlDw8PLBYLNpsNHx+f2nWaNz/5Hz1/f/+TlhUVFREUFFT7uGXLllitVnvKEjdypOoI1t/C92D5\nwd/C+D/hfOJ7a3kBFccqTrsvHw8fwgLC6dryUsL8wwkPiCAsIOz4V/9wBrQZRKhfy0bqTETk7NQb\n5JmZmWRmZtZZlp+fX+exYRgOK+hM9hUSEoCXl+NvhxkWFujwfTZ1Tanno8eOUlBWwC9lv1Bw5Lev\n//v4t69ltrLT7svLw4vwZuFcEnYJEc0iaNW8Ve3XVs1bEdH8P8ta+LVw+eveTek4NyZ37Fs9u596\ngzwuLo64uLg6y5KSkrBarXTp0oWqqioMw6hzNn42QkNDKS4urn1cUFBAeHj4abcpKiq367VOJyws\nEKv1sMP325Q1ds/bCr/ky4Nf/Ha2/J/h7OPD21ZKbSWn3d7D4sF5/mG0D7yQ8IBwwgLCa8+a//dx\niF8IHpaTp4DU6dmAY2VQWHb6PwqcnTv+bIN79q2eXdup/mCxa2g9JiaGrKwsBg4cSHZ2NlFRUXYX\n5u3tTYcOHdiyZQu9e/dm3bp1JCQk2L0/aZrW7XmXhLWjMag74mLBQkv/lvyh+R+4PKAnYf6/DWkH\nHA/n/wR1BKF+ofpgEhGR/2FXkMfGxrJx40bi4+Px8fEhLS0NgMWLF9OnTx8iIyNJTEyktLSUgoIC\nEhISGD9+PJWVlSxZsoTdu3ezfft2li9fzgsvvEBycjIzZsygpqaG7t27Ex0d7dAmxVzfFu1i3Pt3\n4Ovpy6yYR2kf1L42nFv6n6eZ4CIi58BiOPICdyNpiGEUdxqeOaExei6pLGb4G0P5vvg7nr7qOUZ2\nurFBX68+Os7uwx37Vs+u7VRD67qzmzSY6ppqxr0/lu+Lv2PC5febHuIiIq5IQS4NJnXTbNbvfZ8h\nba9ker+ZZpcjIuKSFOTSIN78NpOMzxdwYXAHnh32giapiYg0EAW5ONw2az4PZt9Lc+9AXhqxihZ+\nIWaXJCLisjRdWBzKWm7l1ndvouJYBS+NWEXn0C5mlyQi4tJ0Ri4OY6u2Mfa9BH4q20dS3+kMvzDW\n7JJERFyeglwcZvqGKXz680b+eNH1PNjrb2aXIyLiFhTk4hAvbV/Ki9uXcEnopTw59GmXv3e5iEhT\noSCXc/bpz7lM/fghQnxDeCl2pT7uU0SkESnI5ZzsP/wTt2fdQo1Rw/PXvET7oAvMLklExK1o1rrY\nreJYBYlZN1NYYWXugHkMbDPY7JJERNyOzsjFLoZhMCl7IvnWz4nvcgt3XDbO7JJERNySglzs8vQX\n/8cb375Gr4g+PDb4CU1uExExiYJcztqHez9g9qcziAhoxdLhL+Pr6Wt2SSIibktBLmdld8n33P3+\n7XhZvHhxxApaNWttdkkiIm5Nk93kjB22lTJm7WhKKovJGPoMvSL6mF2SiIjb0xm5nJEao4YJH9zF\nrqKd3BV5D6O73Gx2SSIigoJcztBjnz1K1p61DPzDYGZGzzW7HBER+Y2CXOr1r+/fYsGWx2gXdAHP\nXfMiXh66IiMi0lQoyOW0thd+xcT14wjwasZLI1YS6tfS7JJEROS/6NRKTunXo4e4Nesmyo8dYck1\ny+na8lKzSxIRkf+hM3L5XcdqjnHne4nsLd3D5N5T+ONFfza7JBER+R0KcvldMzdO4+P9OQy/8Fr+\n1meq2eWIiMgpKMjlJCu/eZnFXz5D55AuPHXls3hY9GMiItJU6V9oqWNrwWf8LecBgn1bsCx2JYE+\nQWaXJCIip6Egl1q/HPmZxHdv5phxjMXDltIh+CKzSxIRkXooyAWAo8eOclvWzRSU/8KM/rMZ0u5K\ns0sSEZEzoCAXDMPg7/9+kK0FWxjZ6Ubu6X6v2SWJiMgZUpALz2/7B6t2rODysB6kX5GhzxYXEXEi\nCnI39++fPmLGJ8mE+Yfz4ohX8PfyN7skERE5CwpyN/ZD0Q/c+d6teFg8eGH4y5zf/A9mlyQiImfJ\nriCvqqpi8uTJxMfHc8stt7Bv376T1ikpKWHs2LHcd999dZZv3ryZ/v37k52dXbssISGBG264gYSE\nBBISEvjqq6/sKUvOQllVGX9e9WeKKotIG5ROVOt+ZpckIiJ2sOte62vWrCEoKIj09HQ2bNhAeno6\nCxcurLNOSkoKvXr1YseOHbXL9u7dy9KlS+nZs+dJ+0xNTaVTp072lCNnyTAM7lt/D9sObuO2bneQ\n0DXR7JJERMROdp2R5+bmMmzYMACio6PJy8s7aZ05c+bQq1evOsvCwsJYtGgRgYGB9rysOMgTWx9n\nze63GNR+EHNi5pldjoiInAO7zsgLCwsJDQ0FwMPDA4vFgs1mw8fHp3ad5s2bn7Sdv/+pJ1JlZGRQ\nVFTERRddRHJyMn5+fvaUJvXI+mEtaZvn0KZ5W16Pex3Kvc0uSUREzkG9QZ6ZmUlmZmadZfn5+XUe\nG4ZxTkWMGTOGzp07065dO1JSUlixYgVjx4495fohIQF4eXme02v+nrAw1x4p+Nr6NRPW34m/lz9v\n3/QWYc3CoJnZVTU+Vz/Ov8cdewb37Fs9u596gzwuLo64uLg6y5KSkrBarXTp0oWqqioMw6hzNn62\nTgzTAwwdOpS1a9eedv2ionK7X+tUwsICsVoPO3y/TUXx0SKue+OPHLYdZvGwpbTxuhjApXv+Pa5+\nnH+PO/YM7tm3enZtp/qDxa5r5DExMWRlZQGQnZ1NVFSU3YUZhkFiYiKlpaUAbNq0iY4dO9q9PzlZ\ndU01d71/Gz+U7Oa+HpO4vuMNZpckIiIOYtc18tjYWDZu3Eh8fDw+Pj6kpaUBsHjxYvr06UNkZGRt\nOBcUFJCQkMD48eOprKxkyZIl7N69m+3bt7N8+XJeeOEFRo0aRWJiIv7+/kRERDBx4kSHNunu5nw6\nk4/2fchV7a5matTDZpcjIiIOZDHO9QK3CRpiGMVVh2de3/Uq4z+4k4tbdCTrhg8J8g2ufc5Vez4d\n9ew+3LFv9ezaHDq0Ls4h/+DnTMqeSKBPEC+NWFUnxEVExDXYNbQuTd/B8oPc+u5NVFZXsuSal7g4\nRPMORERckc7IXZCt2sbtWbdw4Mh+pvVLYdgFw80uSUREGoiC3AVN/fhvbP7lU66/+K9M7PGg2eWI\niEgDUpC7mBe/WsLyr5fS7bxInhjylD5bXETExSnIXUjugU9I3vA3Wvq1ZNmIV2jm7Ya3bRMRcTMK\nchfx0+F9jH0vAYAl1yynbWA7kysSEZHGoFnrLqC8qpxb372JwopC0galE/2HAWaXJCIijURn5E7O\nMAwezJ7AtsJ8Eromctuld5hdkoiINCIFuZNb9MWT/PO7N+jTKorUgfM1uU1ExM0oyJ3YBz++x5zc\nFFo3O58Xhr+Mj6f9n0AnIiLOSUHupL4v/pZx79+Br6cvy0a8QkRAhNkliYiICTTZzQltL/yKO9aN\nodRWwlNXLuby8J5mlyQiIiZRkDuRQxWHSNs8h+VfL6XGqGFijweJ6zza7LJERMRECnInUFVdxdKv\nnuPxLWmUVBbTsUUnZg9IZWi7YWaXJiIiJlOQN3Ef7v2Ahzck8W3xLoJ9WzB3wDwSL70Db09vs0sT\nEZEmQEHeRH1f/C0pn0xj3Y9ZeFg8SLx0LFP6Tqelf0uzSxMRkSZEQd7ElFaWsGDr4zz35TNU1VQR\nc/5A5gyYx6XndTO7NBERaYIU5E1EdU01q3asYO6mWRRWWGkX2J6Z0XO5tsMfdZMXERE5JQV5E/Dp\nz7lM3zCFL61fEOAVQHLUDMZ1vxc/Lz+zSxMRkSZOQW6inw7vY3buDP753RsAxHUazfR+M2nd/HyT\nKxMREWehIDdBeVU5T33xJIs+X0jFsQp6hvdizoB59G7V1+zSRETEySjIG5FhGLz13ZvMyn2Y/WU/\nER4QwWODniCu82g8LLpbroiInD0FeSP50voF0zZMYdPPufh4+HB/z8nc33MSzX0CzS5NREScmIK8\ngR0sP0japtms+OYlDAxiL/wjM6PncEHwhWaXJiIiLkBB3kBs1Tae+/IfLNj6GIdtpVwS2pXZA9IY\n1OYKs0sTEREXoiB3MMMweP/HLGZ8kszuku8J8Q0hbVA6Y7rehpeH/neLiIhjKVkcaNevO3n4kySy\n963H0+LJHZfdzd/6TCXEL9Ts0kRExEUpyB2g+GgR87eksWTbYqqNaga1GcKcAWl0Cb3E7NJERMTF\nKcjPQXVNNcu/fpG0zbP59eivXBB0IY/EpHLNBSN0W1UREWkUCnI7fbL/Y6ZtmMLXh76imXdzHu7/\nCHdF3oOvp6/ZpYmIiBuxK8irqqpISkriwIEDeHp6kpqaStu2beusU1JSwqRJk2jWrBkZGRkAHDt2\njGnTprF3716qq6v5+9//Tu/evdmxYwczZ84EoHPnzsyaNevcumpAP5buYdbGh1mz+y0A4rvcQnK/\nFCICIkyuTERE3JFdtxNbs2YNQUFBrFy5knHjxpGenn7SOikpKfTq1avOsrfeegt/f39WrlzJ3Llz\nSUtLA2Du3LkkJyezatUqysrKyMnJsaesBlVWVUbqpkcYsLIPa3a/Re+Ivrx3QzZPDn1aIS4iIqax\nK8hzc3MZNmwYANHR0eTl5Z20zpw5c04K8j/96U9MnToVgNDQUIqLi7HZbOzfv5/IyEgAhgwZQm5u\nrj1lNYgao4bMnauIfqUXT2ydT6hfS5656nne+ev79IjoVf8OREREGpBdQ+uFhYWEhh5/S5WHhwcW\niwWbzYaPj0/tOs2bNz9pO29v79rvly1bxnXXXUdRURFBQUG1y1u2bInVarWnLIfLK9jCtA1T2Frw\nGX6efkzq/Xcm9niQZt7NzC5NREQEOIMgz8zMJDMzs86y/Pz8Oo8NwzirF12xYgXbt2/nH//4B7/+\n+utZ7yskJAAvL8+zes0zERZ2/L7nPx/+manrp7IsfxkAoy4dxWNXPUb7Fu0d/ppmO9GzO1HP7sMd\n+1bP7qfeII+LiyMuLq7OsqSkJKxWK126dKGqqgrDMOqcjZ9OZmYmH374IU8//TTe3t61Q+wnFBQU\nEB4eftp9FBWVn9FrnY2wsED2/Wxl8ZdP88TW+RypKqPbeZHMHTCP/ufHQBVYrYcd/rpmCgsLdLme\n6qOe3Yc79q2eXdup/mCx6xp5TEwMWVlZAGRnZxMVFXVG2+3bt49Vq1axaNEifH2Pv03L29ubDh06\nsGXLFgDWrVvHwIED7SnLboZhsHrHagau6sucT2fi5+lL+hUZvD8y53iIi4iINFF2XSOPjY1l48aN\nxMfH4+PjUzv7fPHixfTp04fIyEgSExMpLS2loKCAhIQExo8fT25uLsXFxdx11121+1qyZAnJycnM\nmDGDmpoaunfvTnR0tGO6OwPlVeUkZt3ER/s+xMvDi7u7T+Ch3lMI9m3RaDWIiIjYy2Kc7QXuJsCR\nwyg/lu5h0KoorrjgCqb3mU3HkE4O23dT505DUieoZ/fhjn2rZ9d2qqF1t7+zW/ugC/j+jv20jghx\nmx8GERFxHXZdI3c1+nhRERFxVgpyERERJ6YgFxERcWIKchERESemIBcREXFiCnIREREnpiAXERFx\nYgpyERERJ6YgFxERcWIKchERESemIBcREXFiCnIREREn5pSffiYiIiLH6YxcRETEiSnIRUREnJiC\nXERExIkpyEVERJyYglxERMSJKchFREScmIJcRETEiXmZXUBDq6qqIikpiQMHDuDp6Ulqaipt27at\ns05JSQmTJk2iWbNmZGRknHa7HTt2MHPmTAA6d+7MrFmzGrulep1Jz2+//TbLli3Dw8ODUaNGERcX\nR3l5OUlJSRQWFuLv709aWhphYWEkJCRQXl5OQEAAAFOmTKFbt25mtHZKju7ZlY9zQUEBycnJ2Gw2\nampqmDp1Kt26dWPo0KG0atUKT09PAObPn09ERIQZrZ2Wo/veuHEjCxYswNPTk0GDBjFhwgSTOjs1\ne3t+5pln2LhxIwA1NTUUFhby3nvvOcWxdnTPznCc7Wa4uDfffNOYOXOmYRiG8fHHHxv333//Sevc\nf//9xlNPPWVMnDix3u1uueUWIz8/3zAMw5g0aZLx0UcfNXQLZ62+no8cOWJcffXVRmlpqVFRUWFc\ne+21RlFRkbF06VLjscceMwzDMD777DNj+vTphmEc73nnzp2N28RZaoieXfU4p6WlGStXrjQMwzC2\nbt1q3H777YZhGMaQIUOMsrKyxm3CDo7ue8SIEcaBAweM6upqIz4+3vj2228bt6EzYG/P/7uP5557\nzjAM5zjWju7ZGY6zvVx+aD03N5dhw4YBEB0dTV5e3knrzJkzh169etW7nc1mY//+/URGRgIwZMgQ\ncnNzG7iDs1dfz/n5+Vx22WUEBgbi5+dHz549ycvLY8+ePbW99e7dm61btzZ67fZyZM+ufpxDQkIo\nLi4GoLS0lJCQkEav/Vw4su99+/YRHBxM69at8fDwYPDgwS51rE84duwYK1eu5JZbbmnUus+FI3t2\nluNsL5cfWi8sLCQ0NBQADw8PLBYLNpsNHx+f2nWaN29+RtsVFhYSFBRUu07Lli2xWq0N3MHZq6/n\n/34eIDQ0FKvVSqdOncjJyeGaa65h8+bNHDhwoHadjIwMioqKuOiii0hOTsbPz69xm6qHI3suKipy\n6eOcmJjIyJEjWb16NWVlZaxcubJ2nZSUFPbv30+vXr2YPHkyFoulcZs6A47s22q1nrTuvn37Greh\nM2BvzyesW7eOAQMG1Pm9berH2pE9O8txtpdLBXlmZiaZmZl1luXn59d5bNh5a/nf287efTmSI3o+\n8fzIkSPZuXMn8fHx9O3bt/YHf8yYMXTu3Jl27dqRkpLCihUrGDt2rAO7ODuN0fPZ7KsxOLLn559/\nnhEjRnDPPfeQnZ3NvHnzWLRoEffddx8DBw4kODiYCRMm8N577zF8+HDHNnKWGrrv22+/3bEFO4Aj\nez7hjTfeqDPPo6kd68bo2ZW5VJDHxcURFxdXZ1lSUhJWq5UuXbpQVVWFYRh1zsZPJTw8/KTtwsLC\naofmAAoKCggPD3d4H2fDnp7Dw8MpLCysfXzw4EEuv/xyfHx8an/wjxw5wvr16wFqh7cAhg4dytq1\naxuypXo1dM+hoaEufZzff/99HnjgAQBiYmJq+7/++utr1x00aBC7du0yPcgbuu//XdfVjjVAeXk5\nv/zyC23atKl9vqkd64buuSkeZ0dy+WvkMTExZGVlAZCdnU1UVJTd23l7e9OhQwe2bNkCHB+6GThw\nYMMUfg7q67l79+5s27aN0tJSjhw5Ql5eHr179yYnJ4eFCxcCx2eDDhw4EMMwSExMpLS0FIBNmzbR\nsWPHxm3oDDiyZ1c/zu3bt6892/nyyy9p3749hw8fZuzYsdhsNgA+++yzJnmcwbF9t2nThrKyMn76\n6SeOHTtGdnY2MTExjd5TfeztGWDHjh106NChdl1nOdaO7NlZjrO9XP5jTKurq5k+fTp79uzBx8eH\ntLQ0WrduzeLFi+nTpw+RkZG1QVVQUEDHjh0ZP348ffv2/d3tvvvuO2bMmEFNTQ3du3dn6tSpZrd4\nkvp67tGjB1lZWSxZsgSLxcItt9zCn/70J44ePcp9991HcXExwcHBLFiwgMDAQNauXcvzzz+Pv78/\nERERzJ07F39/f7PbrMPRPbvycT548CDTpk3j6NGjAEybNo0uXbqwbNkyVq9eja+vL127duXhhx9u\nctdNwfF9f/bZZ8yfPx+Aq6++2tTLRqdib89A7Vuv/nuY2RmOtaN7dobjbC+XD3IRERFX5vJD6yIi\nIq5MQS4iIuLEFOQiIiJOTEEuIiLixBTkIiIiTkxBLiIi4sQU5CIiIk7s/wFIoMruVJAkAwAAAABJ\nRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jrsUps0nu8vj",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "** Question **
\n",
+ "Why did I created a session to plot the graph?
\n",
+ "[Ans]"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "P3-iuxE4sjAf",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the placeholders\n",
+ "\n",
+ "# Placeholders?\n",
+ "# The input to the model changes on iteration\n",
+ "# So we cannot have a constant in the input as we did before\n",
+ "# And thus we need placeholders which we can change on each \n",
+ "# iteration of the training\n",
+ "\n",
+ "x = tf.placeholder(tf.float32, name='x')\n",
+ "y = tf.placeholder(tf.float32, name='y')"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "8hPRkaoxvRyV",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 88
+ },
+ "outputId": "53ba8b0a-4c2b-4b3b-8276-33ca71690ef1"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the linear regression model\n",
+ "\n",
+ "# tf.Variable?\n",
+ "# We define the model parameters as tf.Variables\n",
+ "# as they get updated throghout the training.\n",
+ "# And variables denotes something which changes overtime.\n",
+ "\n",
+ "W = tf.Variable(np.random.random_sample(), name='weight_1')\n",
+ "b = tf.Variable(np.random.random_sample(), name='bias_1')\n",
+ "\n",
+ "pred_y = (W*x) + b"
+ ],
+ "execution_count": 16,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow/python/framework/op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.\n",
+ "Instructions for updating:\n",
+ "Colocations handled automatically by placer.\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "cSw1P8bkv96r",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the loss function\n",
+ "# We are going to use the mean squared loss\n",
+ "loss = tf.reduce_mean(tf.square(y - pred_y))"
+ ],
+ "execution_count": 0,
+ "outputs": []
+ },
+ {
+ "metadata": {
+ "id": "5G4uQqjsygNj",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 88
+ },
+ "outputId": "1a675063-607c-4a96-fd95-e9652296eac8"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Let's define the optimizer\n",
+ "# And specify the which value (i.e. loss) it has to minimize\n",
+ "optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)"
+ ],
+ "execution_count": 18,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow/python/ops/math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.\n",
+ "Instructions for updating:\n",
+ "Use tf.cast instead.\n"
+ ],
+ "name": "stdout"
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "ttI7ZT-ozAm1",
+ "colab_type": "code",
+ "outputId": "9d1eab03-3851-4be7-a50b-1a7147eeb841",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 432
+ }
+ },
+ "cell_type": "code",
+ "source": [
+ "# So the graph is now built\n",
+ "# Now let's execute the graph using session\n",
+ "# i.e. lets train the model\n",
+ "\n",
+ "# What it is to train a model?\n",
+ "# To update the paramters in the graph (i.e. tf.Variables)\n",
+ "# So that the loss is minimized\n",
+ "\n",
+ "# Okay let's start!\n",
+ "with tf.Session() as sess:\n",
+ " # We need to initialize the variables in our graph\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ " \n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x:train_X, y:train_Y})\n",
+ " \n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ " \n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x:test_X, y:test_Y})\n",
+ " \n",
+ " \n",
+ " print ('The final loss is: ', final_loss)\n",
+ " \n",
+ " # Plotting the final predictions against the true predictions\n",
+ " plt.plot(test_X, test_Y, 'g', label='True Function')\n",
+ " plt.plot(test_X, final_preds, 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()"
+ ],
+ "execution_count": 22,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.07394742\n",
+ "Loss after epoch 20 is 0.07394247\n",
+ "Loss after epoch 40 is 0.073937505\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.24076582\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeEAAAFKCAYAAAAqkecjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3Xl8VPW9//HXZN8my4RJQhLCEiCQ\nYBBEFJBVUKt1qVoFRbRg3VBbq9clLmhbEC1669IqIrX+FDGK0eJS8VrBpSCgskgEAgGyEMi+78v5\n/REcCdlITHKS4f3kkUdyOOd8z+eTmTPvzJmZcyyGYRiIiIhIj3MxuwAREZFTlUJYRETEJAphERER\nkyiERURETKIQFhERMYlCWERExCRuPb3B3NzSnt5kE0FBPhQWVphaQ3dz9h7VX9/m7P2B8/eo/jrO\nbre2+P+n3DNhNzdXs0vods7eo/rr25y9P3D+HtVf1znlQlhERKS3UAiLiIiYRCEsIiJiEoWwiIiI\nSRTCIiIiJlEIi4iImEQhLCIiYpIeP1lHb/Tcc//L3r27KSjIp6qqivDwCPz9A1iy5C9dMv6VV15M\nSEgoLi4//c3z/PMv/exxv/rqc846ayIlJcWsXLmce+998GePKSIiPeekQjglJYXbbruNG264gblz\n5zaZt3HjRp5++mlcXV2ZMmUKCxcu7JZCu9Mdd9wFwEcfvc+BA6ncfvvvu3wby5Y9i4+PT5eO+eab\nqxg79kyCg/spgEVE+qB2Q7iiooI//elPTJgwocX5f/7zn1m5ciWhoaHMnTuX888/n6FDh3Z5oWb4\n7rtvePPN16moqOD22+/i7rtv58MP/wPAQw/dy+WXX8WIESNZsuQxSktLqa+v5/e//x+GDh12UuNf\ndNG5zcbbtu1bysvLSE9P4/DhTO68824mTJjExx9/yJo1iVgsFmbPvpba2lp++GEX99xzJ/ff/zCP\nPfYQK1e+xnfffcMrryzHMCzY7SE88MAjfPrpOnbu3E5RUSHp6Wlcc811/PKXl3Xb701ERE5OuyHs\n4eHBihUrWLFiRbN5GRkZBAQE0L9/fwCmTp3Kpk2bflYIP7rxId5Pfa/T67fk4ujLeHTinzu1bmrq\nflavTsLDw6PF+W+9tZqzzprIxRdfxsGDB3jmmWX89a9//znlkpOTzbJlz/L11xv517/eYfTo0/nn\nP1/m1VdXU1NTy+LFi1i69GlefvlFli17luLiIse6y5Y9zv/7f6/i5ubH008/wf/938dYLBZSU/fz\n4ov/IDMzg0WLEhTCIiInyKnI4ZujW/A4CueGXoTFYun2bbYbwm5ubri5tbxYbm4uNpvNMW2z2cjI\nyGhzvKAgnzbPy+nj7YGLS9c27uPt0eTk2a2dSNtq9cLH56dlAwN9iI0dSUREMAAWi8Uxz9PTncBA\nH/buTaagoID16z8BoLq6stn4rq4uPPDAXbi6NvYdFBTEs88+2+J4vr6eTJhwFna7lZiYwVRXV1Jc\nnMOwYUOJjLQDsHLlCse4/fr54epai5ubC+7u9bi5uTr+KJo2bTJbt24lNjaWM888g7CwQKxWdyor\ny1v9HfQVfb3+9qi/vs/Ze+zr/dXW17IzeyebMjc1fmVs4mDRQcf8o3cfJcQvtNvr6PE3ZrV3ZYp7\nxzzCvWMe6fLt/nj1Jrvd2uqVnEpLq6ioqHHMLyqqwDAsjmnDMBw/l5dXOubfccfdjBoV32xbP6qv\nb+Dxx/+3yWvCubmlLY5XXl6Nu7s3ubmlFBaWU1NTR3FxFVVVNS2Om5dXRnFxOXV1DeTnl1NXV+8Y\nPz+/hKqqOkpLq6ipaSA3t5SKigrq6xtMv5rVz9HWbegM1F/f5+w99tX+autreWXXCj48+D7bc76j\nsq7SMS/QM5Bzo2YxLmw8l8dfgkulD7mVXddja3+0/KwQDgkJIS8vzzGdnZ1NSEjIzxmyV7NYLFRV\nVQGQkrIXgNjYUXzxxQZGjYrn4MEDbN68kdmz57Y1TJvjtWTgwEGkp6dRUVGBq6sr9913F//7v3/D\nYnGhvr7esZy/vz8Wi4WsrCzc3a1s3/4d8fGnN1lGRORUtPHwV9z/5d3sKdiNBQsjbLGMCxvPmWHj\nGRc6nujAoY7Dzz35R8bPCuHIyEjKysrIzMwkLCyM9evXs2zZsq6qrde57LIruemm6xk0aAgxMSMB\nuPLKq1m8+FFuu+1GGhoa+P3v7/lZ47XE29ubBQtu4fe/vw2Aq6++BovFwpgxY7nttgU8+OCjjmXv\nvfch7r77bhoaICIiknPPPY9PPvl35xoWEenjsiuyeWzjQ6xJScSChXmx83ngrIcJ9g42uzQALIZh\nGG0tsGvXLp544gkOHz6Mm5sboaGhzJgxg8jISGbNmsXWrVsdwXveeeexYMGCNjdo9iGMvnoYpSOc\nvUf117c5e3/g/D32hf7qG+r5Z/LLLNn8J0prSoi3n86TU55mbOi4dtftjv46fTh61KhRvPbaa63O\nP/PMM0lMTOx8ZSIiIl3om6NbuO+Lu/k+bwf+HgEsnfIU18fOx9Wl9TcFm0VnzBIRkT6jwWiguLqI\nwqoCCqoKfvpe3fjzgaID/Cs1CYCrY67hkQl/wu5jN7nq1imERUSkV6pvqGdv4R62ZX/Ldznfsj3n\nO3YXJFPXUNfmeiNtsTwx5WnODp/YQ5V2nkJYRERMV9dQx6HigyTnf8932d+yLedbduZup6Lup4+1\nerl6Ed9vNCG+Ydg8bQR5NX7Zjn0P8gzC5h3MsMDhvfLQc0sUwiIi0mN+DNs9BbtJKdzD3oLd7CnY\nQ2rRPmoaahzLuVhciAkaydjQMxgTcgZjQsYywhaLu6u7idV3PYWwiIh0iQajgbzKPI6WZ3Gk/AhZ\nZYeP+zmLo+VZHCo+2CRsAXzcfInrN4rhQSMYGRzH2JAzGGWPx8/dz6ROeo5CGDhyJIt582YTEzMC\ngJqaGq699nqmTp3e4bHeeSeRoqIipkyZxhdfbGDBgptbXO7HyxC6u7f/V92BA/t5+uknm13+cOrU\nszjttNGO6eDgYB577PEO13yi9es/Zfr0mezbt7fNHkREAFIK9vLy9y/ydkoi5bVlrS4X5BlEbHAc\nMbaRxNhGMsI2guFBI4i0DsDFcmpe3l4hfExU1EBHyJWUFPOb31zL2WdPwNPTq1PjDRsWw7BhMa3O\n//EyhCcTwq3x8/PrkusSn+j1119l+vSZ7fYgIqeuBqOB/6R9wks7X+DzzPUAhPtGMG3ADMJ9wwnz\nC6e/b3/CfSMI8+tPf99wvN28Ta6691EIt8DfP4Dg4H7k5+fzyisrcHNzp6SkiD/+cSlPPrmYrKzD\n1NXVceONt3DGGWfyzTdbePbZp7DZggkO7kd4eATfffcNSUlv8ec/P9nmZQifeeYF1q59l08//RiL\nxYXJk6cxZ85ccnKyefjh+3F3d2fo0OEnXfuRI1ncfPMDLF/+KgALFlzHn//8BP/4x0v062dn797d\nZGcf5ZFH/kxMzAhWrXqVDRv+g8Xiwi233M6ePT+wf38KCQn/w5VXXu3o4T//+T8SE1fh6upKTMxI\nfv/7e1i5cnmLl10UEedVWlPCG1//g2e+fpaDxQcAmBh+DjeedgsXDL4QNxfFSkf0ut+W76MP4fl+\n117KsPriyyh/9OQvZXjkSBYlJcWEhDReQcPf35/77nuQjz/+kODgfjzwwCMUFRXxu9/dwquvvsny\n5c/z8MN/Ytiw4dxzz52Eh0c4xqqoKG/zMoS5uTls2PAf/v73lQDceusCpk+fSVJSIueeex5XXTWH\n11//J/v3p/zs30NNTQ1PP/087723ho8//hAfHx82bPgPy5f/k6ysw7z++j+5//6HWbXqVZYs+Qvf\nfffNsR4qeOmlv/HKK2/g4+PDvffe5Zh34mUXFcIizscwDHbmbidx7xus3rOK8toyPF09uWbEdSyI\nv5nT+sW3P4i0qNeFsFnS09O4/fabgMZrKD/00GOOSzjGxsYBsGvXTnbs2MbOndsBqK6upra2liNH\njjBsWOOz1dNPH0t1dbVj3EOHDhIVNQhPTy88Pb1YuvTpJtvdvTuZzMwM7rij8XXXiopyjh7N4tCh\ng0yfPhOAMWPG8fXXG5vVXFZW5qgZIDp6aJsXjxg9egwAdnsoP/yQTErKXmJjR+Hi4kJk5ADuv//h\nFtfLyEgnMjLKcRWoMWPOICVlDwDx8acDjRfzKCtr/bUgEelb6hvq2XxkEx8dfJ+PDnxAZlnjZWr7\n+4aTMPkBLh94Ta85/3Jf1utCuPzRP3foWWtXOf414RO5ubk7vs+bN59Zsy5oMt/F5ac3FJx4Km4X\nF1cMo6HV7bq5uTNhwiTuvffBJv+/atWrWI69UaG19Vt6Tfjo0SNNpuvqfvpQ+4/XM/6xTldXFxoa\n2jx1OAAWS9O+6upq8fT0bHFMEem7quur+TJzAx8eeJ91hz4ir7LxKnlWD3+uGHYVv4y+lPMGXkB4\nmK3Xnzu6r+h1IdybxcaO4quvPmfWrAsoLCzgrbdWc/PNC+nXz056+iEGDBjItm3fEhd3mmOd9i5D\nGBMzkhdeeI6qqio8PT155pmnuPXW24mKGsiePT8wYsRIx6Hfk+Hj40t+fj6GYVBQkE9WVmary8bE\njOSf/1xJXV0dJSXF/OUvj/P448uaBfOAAQPJzEynoqIcHx9ftm37juuvX8A332zu+C9RRLpcZmkG\n/z74AcXVxVTVVVFVX0ll3U9fVXWVVNVVUWc0/lFuGAYGhuM7x35OKUyhrLYxXPt527ku9jdcNORi\nzomYgoerh4kdOi+FcAfMmDGT777byi23zKe+vp758xsPBd9002089NB9hIX1d7yO/KP2LkP43HMv\ncdVVc1i48Le4uLgwZco0PD29+PWv5/Dww/fzxRfriY4edtI1+vv7M3HiRG68cR5Dhw5r893N/fuH\nc/75F3L77TdhGAY337wQgOHDY/jtb+dx6613OnpYuPB33H33HVgsLsTHn87o0acrhEVMZBgG32Rv\n4aUdL/DBgX9Rb7R/3XALFsc1c3/82fHPYiHMtz9zY6/nwiEXc2bo+D5z1qm+rN1LGXY1sw9h9IVL\ncP1czt6j+uvbnL0/6N4ea+tref/Ae7y04+98l/MtAHHBpzH/tN8y0H8QXq7eeLt74+3qjZebF95u\nPni5eeHl6tVloerst2GvupShiIiYr6Aqn9d/eJWV37/EkfIsLFi4YPBF3Bx/GxPDz3E8w5W+RSEs\nItJLGIZBTkU2aSVppJceIr0kjfSSNDJK0/kmewuVdZX4uvtxU/ytLDjtZgYHDDG7ZPmZFMIiIj2g\noraC7IqjZFdkk1N+tPHn8uxj/3eUw6WZZJSmU1Vf1eL6QwKiuWHUAq4ZcR3+ngE9XL10F4WwiEgX\nazAa+D5vJxsPf8l/D3/JlqNfU1BV0OY6QZ5BxNhGEuU/kAHWKKL8BzLQOpAo/0FEWgfolI9OSiEs\nIvIzNRgN7M7/gY1ZX/LV4S/5+sh/KawqdMyPsg4k3n46oT5hjV++oYT6hBHiG0aoT+PPPu4+JnYg\nZlEIi4h00r7CFP6x6yXe3bemyTPdQYGDOH/QhUwKn8zEiHMYYI0ysUrpzRTCIiIdUN9QzydpH7Py\n+5f44tjVg0J9wrg65homRUxmYvg5nBE9yqk/wiNdRyEsInISCqryWbX7Nf6562UyStMBmBQ+mfmn\n3cQvBl+kqwdJp+heIyKnnB/PNvX23jdZm/ouVXXVBHsHY/MKxuZlI8jLRrBXMDbvYIK8bOzI2ca7\n+9ZQVV+Fj5sP82Lns+C0mxgZHGt2K9LHKYRF5JSRVnKINSmJvLV3teNauHbvEKIDB1BQlU9K4R4q\n6ypbXHdwwBDmj/ots0dcS4BnYE+WLU5MISwiTq2kupi1qe/x1t7VfH2k8ZKg3m7eXD7s11wVM4cp\nkdOaHEquqK2gsKqAgqp88qvyKajKJ9irH5Mjp+JicWltMyKdohAWkT6vsq6S9JI0DpUc5FDxAdJK\nDnGo+CCHSg6SVnKI2oZaAM6JmMJVMXO4aMjFWD38WxzLx90HH3cfIqyRPdmCnKIUwiLS69U11JFV\ndpj00jQyStJJKz1ERkk66aWNp3U8Up7V4npBnkHE20dz/qALuWL4VfqokPQ6CmER6XVKqotZd+jf\nfHBgLcl533O4LLPFS/W5WFwI943gnIgpDPIfzKCAwQzyH8xA/0EMChis126l11MIi0ivUFxdxL8P\nfsgHqf9iQ8Zn1DTUAI2fwR0bOo4o60Ci/KOIsg5ynNoxwi8Sd1d3kysX6TyFsIiYprCqgI8PfsT7\nqe/xeeZ6x2u3scGjuCT6Mi6OvoxhQcNNrlKk+yiERaTbNBgN5FRkc6jkkOMNU9k1h9mTnUJaySFy\nK3Mcy47qF38seC8lOnCYiVWL9ByFsIh0ifLacn7I38X3eTtJzvue73N3sLeVz926ubgR6TeA2ODp\nTI6cyi+jL2VIQLQJVYuYSyEsIh3WYDTwbfZWNmVtJDlvJ9/n7SS1aD8GhmMZdxd3hgeNYEhgdOMb\npY69YeqMwafhVROo0zyKoBAWkZNU11DH10c28kHqv/jo4AccLT/imOfvEcCE8EmM6ncao/rFM6pf\nPMODYvBw9Wg2jj3IqosbiByjEBaRVlXXV/NV5ud8cGAtHx/8kPyqfKDx87dzRsxl5sDzOK3faAb6\nD8JisZhcrUjfoxAWOUVllmaQW5FDYXUhxdVFFFUXUVxdRGFV43R+VR4bs/5LaU0J0HiO5evjFvDL\nIZcwMfwcfTRIpAsohEVOIYVVBSTte5s3dr/O93k72l0+0m8A14yYy0XRl3Jm6HhcXVx7oEqRU8dJ\nhfCSJUvYsWMHFouFhIQE4uPjHfM+/fRTXnjhBTw8PLjooouYO3dutxUrIh1X31DPF5kbWL3nNT46\n8AE1DTW4ubhx3sALiA4cRqBnIIFeQQR6BhLgGdg47RlIgGcQNi+bDjOLdKN2Q3jLli2kpaWRmJhI\namoqCQkJJCYmAtDQ0MCf/vQn3n33XQIDA/ntb3/LzJkzCQsL6/bCRaRtaSWHeHPPKhL3vEFmWQYA\nw4NiuGbkPK4cfjUhPiEmVygi7Ybwpk2bmDlzJgDR0dEUFxdTVlaGn58fhYWF+Pv7Y7PZADj77LPZ\nuHEjl19+efdWLSKUVBeTWZZJZmk6mWWZHC7N5HBZBpmlmRwua/wC8HO3cl3sDcwZMZczQs/UM1uR\nXqTdEM7LyyMuLs4xbbPZyM3Nxc/PD5vNRnl5OYcOHSIiIoLNmzczfvz4bi1Y5FSVVnKIrzK/4MvD\nn/Pfw1+SXXG0xeVcLa6E+0UwbcAMrhh2Fb+MvhRfd98erlZETkaH35hlGD99GN9isbB06VISEhKw\nWq1ERrZ//c2gIB/c3Mx9c4fdbjV1+z3B2Xs8FfrLKs1i/cH1fHbwMz479BmHig455of6hnLRsIsY\nGDCQqICoJl/9rf17/YkwnP32A+fvUf11jXb31JCQEPLy8hzTOTk52O12x/T48eN54403AHjqqaeI\niIhoc7zCworO1tol7HbnP1GAs/forP0ZhsHugh/4NOtD3t61hr2FexzzAj0DuXDwxUyOnMI5EVMZ\nHhTT8mHlGijMb36ayN7EWW+/4zl7j+qvc2O2pN0QnjRpEs899xyzZ88mOTmZkJAQ/Pz8HPNvvPFG\nnnjiCby9vVm/fj2/+c1vuq5qkVPAnoLd/Gt/Emv3v8u+ohQAvN28OTdqFudETGVy5BTigk/Tx4NE\nnFC7ITx27Fji4uKYPXs2FouFRYsWkZSUhNVqZdasWVx11VXMnz8fi8XCTTfd5HiTloi0rLq+mgNF\nqbyf+h5rU98lpXAvAF6uXvxyyKVcN/YaxgdN0eu4IqcAi3H8i7w9wOxDGM5+GAWcv8fe1l+D0UBu\nRQ7ppWmkl6SRUZpOdsVRiqoaz0BVXFPc+L268XtVfZVjXS9XL84deB6XRv+KmYPOx8/dr9f119Wc\nvT9w/h7VX+fGbEnvfveGSC+TW5HL+wfeY3f+D6SXHCKjNJ3M0owmwXoiV4srAZ4BBHgGEu4Xjr9H\nAHafEGYOPI/zBl6An4dzv8FFRFqnEBZpR0VtBf8++AFrUhLZkPEZ9Ua9Y57Ny0aMbSRR/gMZYI0i\nyn8gUdYownzDCfIMIsAzAF93P302V0RapBAWaUF9Qz1fHv6cNSmJfHjgfcprywA43T6GK4dfzaSI\nKUT5R2H18De5UhHpyxTCckprMBrIrczlaFkWR8qPcKQ8i/2FKaxNfc9xMowo60Bujr+VK4ZfzbCg\n4SZXLCLORCEspwTDMEjO38WGjM/YnvMdWWWHOVKeRXbFUeoa6potH+gZyLzY+fw6Zjbjw87S4WQR\n6RYKYXFaORU5fJ7xGRuOfeVW5jjmubm4EeoTxmj7GPr7htPftz9hfuGE+4YT4RfJmNAz8HT1NLF6\nETkVKITFaZRUF/NN9la+zPycDRmfkZz/vWOe3TuEXw+fzbQBM5gYfg5hvv118gsRMZ1CWPokwzA4\nWHKArUc2s/XoFrYe3cyegh8waPzYu6erJ1MjpzNtwLlMGzCD2OA4HVIWkV5HISx9QlVdFTtyt7P1\n6GZ2Fn7LV2n/Ja8y1zHfx82HieHnML7/WZzVfyITwifh7eZtYsUiIu1TCEuvlF1+lC1HN7P12NfO\n3O3UNtQ65kf4RXLZ0MsZH3Y2Z4adRWzwKNxd3U2sWESk4xTC0itklmbwecZ6vjr8BVuzt5Becsgx\nz9Xiymn94jkz7CzODDuLC+LOxasm0LxiRUS6iEJYTFFSXcxXh7/k88zP+CJzA6lF+x3zgjyDOG/g\nBY7QHR0ypsnFDOwBzn3eWhE5dSiEpVvUNdQdu2BBIUXHXbxgT+FuvsjYwLacbx2nf/R19+P8Qb9g\nSuQ0pkROb/1auSIiTkYhLJ2WX5nP7oJkducnszv/B3YXJJNdnk1RdRFlta0/U3W1uDI2dBxTIqcx\ndcAMzggZp9dzReSUpBCWdpXXlrOvcC97CnY7wnZ3/g+O0zr+yN3FnTDf/gwKGEygZyD+HgEEegYS\n4BnY+N0rkAi/SCb0n4i/Z4BJ3YiI9B4KYXEoqy1jf2EKewp2k1K4l70Fu9lbsIf00rRmy0b6DWDW\nwPOJDR7FyOBYRtriGBo4TM9oRUQ6QCF8isutyGVt6ru8t/8dthz52nGyix/ZvUOYHDGV4bYYYoJG\nMjI4jpG2kXomKyLSBRTCp6CS6mI+OvgBSfve5svMz6k36rFg4cyws4i3j2Z40AhG2EYy3BaDzSvY\n7HJFRJyWQriPq6yr5O29b7Jq96vUNdRj97ETZYvEagnC7mMnxCcUu3cIdp8Q9hXuJWnfGj5NW0d1\nfTUAY0PO4FfDruTSoZcT5tvf5G5ERE4tCuE+Krcil1d2reCfyS+TV5mHm4sbHi6efJ+3A9LbXjcm\naASXD/s1lw27gsEBQ3qmYBERaUYh3MekFOzlxR3P83bKm1TXVxPoGcjvx97D/NN+S5hvf8pqy2jw\nqmBP5kFyKrLJrcwhpyKbnIoc+nkHc0n05bqYgYhIL6EQ7gPqG+r5b9aXvLD9Of6T/n8ADPIfzM2j\nFzJ7xLVNzibl5+6H3dYf//oQs8oVEZGTpBDupdJL0vg8cz2fZ6zny8wNFFYXAnBW/wncMvp2Lhh0\noa6HKyLSxymEe4ni6iK+zPziWPB+xqGSg455EX6RXDjkYq6LvYGxoeNMrFJERLqSQrgH1DfUk1OR\nTVb5YY6UHeFI+WGyyrI4Un6YI+VHyCo7TEZpOg1GAwBWD38uGHwRUyOnMzVyOtGBQ/UaroiIE1II\nd5O6hjo2Zn3Fe/ve4YMD/6KouqjF5SxYCPEJZXzY2UyOnMrUyBmMDT0DNxfdNCIizk6P9F2owWhg\ny9HNvLdvDWtT3yOvMheAUJ8wLht6Of19Iwj3C6e/bzj9/cIJ940gxCdUp3oUETlFKYR/ptr6Wr7P\n28G/9r/Lv/YnkVV+GIBgr2Cuj1vAr4ZewVn9J+hNVCIi0oxCuAPqG+rZV5TC9pzv2JG7je0520jO\n+56q+iqg8bXc2SOu5bKhVzA5Yqqe4YqISJsUwicwDIOSmmIySzM5XJZBRmkGB4tT2ZG7ne9zd1BR\nV+FY1s3FjZG2OE4PGcPMgeczI2omnq6eJlYvIiJ9ySkdwvmV+Xx08H125GzncFkGh8syySzNbPGC\n9C4WF2KCRnJ6yBhGh4zhdPsYYoNH4eXmZULlIiLiDE65EC6qKmL17tW8t/8dvsjcQL1R75gX4BlI\nlP9AIv0iibBGEuE3gEhrJAOsUcQGj2pyZioREZGfq8+HcPGxj/74uvu1+rGesppSPj70Ee/te4f1\nGf+htqEWgNPtY7h06BVMjzqXAdYBWD38e6xuERGRPh3Cm7L+y2XvXei4EL2nqye+7r74uvvh5+6H\nj7sv7i7ubM/5zvHmqfjQeC4e9CsuGforXUFIRERM1adDeGjgcK4dOY+8ylzKa8spry079r2co+VH\nKK8tp6ahhuFBMVw69HIuG3oFE4efQW5u89d8RUREelqfDmG7j52npz/X5jJ1DXU6+5SIiPRKLmYX\n0N0UwCIi0ls5fQiLiIj0Vif1NHHJkiXs2LEDi8VCQkIC8fHxjnmrVq1i7dq1uLi4MGrUKB588MFu\nK1ZERMSZtPtMeMuWLaSlpZGYmMjixYtZvHixY15ZWRkrV65k1apVrF69mtTUVLZv396tBYuIiDiL\ndkN406ZNzJw5E4Do6GiKi4spKysDwN3dHXd3dyoqKqirq6OyspKAgIDurVhERMRJtHs4Oi8vj7i4\nOMe0zWYjNzcXPz8/PD09WbhwITNnzsTT05OLLrqIwYMHtzleUJAPbm7mXlHIbreauv2e4Ow9qr++\nzdn7A+fvUf11jQ6/ddgwDMfPZWVlLF++nI8//hg/Pz+uv/569uzZw4gRI1pdv7CwotV5PcFutzr9\n54SdvUf117c5e3/g/D2qv86N2ZJ2D0eHhISQl5fnmM7JycFutwOQmprKgAEDsNlseHh4MG7cOHbt\n2tVFJYuIiDi3dkN40qRJrFu3DoDk5GRCQkLw8/MDICIigtTUVKqqGk8JuWvXLgYNGtR91YqIiDiR\ndg9Hjx07lri4OGbPno3FYmEOwgL+AAAWLElEQVTRokUkJSVhtVqZNWsWCxYsYN68ebi6ujJmzBjG\njRvXE3WLiIj0eRbj+Bd5e4DZryM4+2sZ4Pw9qr++zdn7A+fvUf11bsyW6IxZIiIiJlEIi4iImEQh\nLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWw\niIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIi\nIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuI\niJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJnE7mYWWLFnCjh07\nsFgsJCQkEB8fD0B2djb33HOPY7mMjAzuvvtuLr744u6pVkRExIm0G8JbtmwhLS2NxMREUlNTSUhI\nIDExEYDQ0FBee+01AOrq6rjuuuuYMWNG91YsIiLiJNo9HL1p0yZmzpwJQHR0NMXFxZSVlTVb7t13\n3+X888/H19e366sUERFxQu2GcF5eHkFBQY5pm81Gbm5us+Xefvttrrzyyq6tTkRExImd1GvCxzMM\no9n/bdu2jSFDhuDn59fu+kFBPri5uXZ0s13Kbreauv2e4Ow9qr++zdn7A+fvUf11jXZDOCQkhLy8\nPMd0Tk4Odru9yTIbNmxgwoQJJ7XBwsKKDpbYtex2K7m5pabW0N2cvUf117c5e3/g/D2qv86N2ZJ2\nD0dPmjSJdevWAZCcnExISEizZ7zff/89I0aM6IIyRURETh3tPhMeO3YscXFxzJ49G4vFwqJFi0hK\nSsJqtTJr1iwAcnNzCQ4O7vZiRUREnMlJvSZ8/GeBgWbPet9///2uq0hEROQUoTNmiYiImEQhLCIi\nYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiI\nSRTCIiIiJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiIm\nUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhE\nISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhK3\nk1loyZIl7NixA4vFQkJCAvHx8Y55R44c4Q9/+AO1tbXExsbyxz/+sduKFRERcSbtPhPesmULaWlp\nJCYmsnjxYhYvXtxk/tKlS5k/fz5r1qzB1dWVrKysbitWRETEmbQbwps2bWLmzJkAREdHU1xcTFlZ\nGQANDQ18++23zJgxA4BFixYRHh7ejeWKiIg4j3YPR+fl5REXF+eYttls5Obm4ufnR0FBAb6+vjz+\n+OMkJyczbtw47r777jbHCwrywc3N9edX/jPY7VZTt98TnL1H9de3OXt/4Pw9qr+ucVKvCR/PMIwm\nP2dnZzNv3jwiIiK46aab2LBhA9OmTWt1/cLCik4V2lXsdiu5uaWm1tDdnL1H9de3OXt/4Pw9qr/O\njdmSdg9Hh4SEkJeX55jOycnBbrcDEBQURHh4OFFRUbi6ujJhwgT27dvXRSWLiIg4t3ZDeNKkSaxb\ntw6A5ORkQkJC8PPzA8DNzY0BAwZw6NAhx/zBgwd3X7UiIiJOpN3D0WPHjiUuLo7Zs2djsVhYtGgR\nSUlJWK1WZs2aRUJCAvfffz+GYTB8+HDHm7RERESkbSf1mvA999zTZHrEiBGOnwcOHMjq1au7tioR\nEZFTgM6YJSIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEs\nIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCI\niIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIi\nIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iI\nmEQhLCIiYhK3k1loyZIl7NixA4vFQkJCAvHx8Y55M2bMICwsDFdXVwCWLVtGaGho91QrIiLiRNoN\n4S1btpCWlkZiYiKpqakkJCSQmJjYZJkVK1bg6+vbbUWKiIg4o3YPR2/atImZM2cCEB0dTXFxMWVl\nZd1emIiIiLNrN4Tz8vIICgpyTNtsNnJzc5sss2jRIubMmcOyZcswDKPrqxQREXFCJ/Wa8PFODNk7\n77yTyZMnExAQwMKFC1m3bh0XXHBBq+sHBfng5uba8Uq7kN1uNXX7PcHZe1R/fZuz9wfO36P66xrt\nhnBISAh5eXmO6ZycHOx2u2P6sssuc/w8ZcoUUlJS2gzhwsKKztbaJex2K7m5pabW0N2cvUf117c5\ne3/g/D2qv86N2ZJ2D0dPmjSJdevWAZCcnExISAh+fn4AlJaWsmDBAmpqagDYunUrw4YN66qaRURE\nnFq7z4THjh1LXFwcs2fPxmKxsGjRIpKSkrBarcyaNYspU6Zw9dVX4+npSWxsbJvPgkVEROQnFqOH\n30ll9iEMZz+MAs7fo/rr25y9P3D+HtVf58Zsic6YJSIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwi\nImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIiJlEIi4iImEQhLCIiYhKFsIiI\niEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImUQiLiIiYRCEsIiJiEoWwiIiISRTCIiIi\nJlEIi4iImEQhLCIiYhKFsIiIiEkUwiIiIiZRCIuIiJhEISwiImIShbCIiIhJFMIiIiImcTO7ABER\nOYUZRvtfJyxnoa3lm4/ZZPmT2aZbFD0Vjwph6ZiO3JGPW6bTO01L26nwxSWvtOV1HMufRH3N1jm5\nGlvspa0xMLC01/Px6/t74VFc0bitDjww/TjdsXWMVtZppR9OYjutbAODxnW83fEtr27z93XieC3W\n1+T+2MJt2+bvoYVeW9zOcf20ch9usTZ3FwJq6lodq+XttPT7o/VttbVPHb/vNfmdndxtZmlzG43j\nBDe0sJ029/MTxu/NPD2xbN+DERzc7Zvq0yFsyc7Gd8ljuJQ2f0Bu9c7g7kpAde0Jdzxa3fnb3KGb\nbYPmd7Tjx+roDtDWTtPaDnNMcEPDCTsNLa/XR3ea7t81zBVgdgHdzMfsAnqARxvzDIsFWvuCE6Yt\nrSxPC+s2fjdaGufELxeXY8vj2O6P22m7Pgsu7q401ButbKd5/SeO4Ri/pRppbZw2fm8tbKNpHzRd\nto3fjWGx4B09CCMo6OffCU5Cnw5h14MH8HprNZb6+g6t19bO0Zo275Qnu8NAy3eeY//f7jZO2Gla\n22FcXF1oaDCa30Fb3Q7Na2r1ztx0p2hrp2nzgaBDOw1Nlvfy9qCquq712prV1UptJ67TSk3N12tp\n/NZ7/ekBp7VxabK+n9Wb0vLqdtZpvs02H9jaXaet7Zx4/zi2P7S1Tgs1GMeWD7L5UlhU0f7vmrbH\na/7/NF/vJL5a3w5tbr+t7dhD/MnNK2u5Xidgt1spzC01u4xu4223Qg/116dDuO7sCeSnpEF1TcsP\nFi3sMM12Dlpfp6/uNM6+g3jZrZQ6cX9+ditVTtwfdit1ztwfgLs7uPXph1fpIX3+XmJY/cHagRV8\nfMC7Y8+cRUREuoM+oiQiImKSkwrhJUuWcPXVVzN79mx27tzZ4jJPPfUU1113XZcWJyIi4szaDeEt\nW7aQlpZGYmIiixcvZvHixc2W2b9/P1u3bu2WAkVERJxVuyG8adMmZs6cCUB0dDTFxcWUlZU1WWbp\n0qXcdddd3VOhiIiIk2o3hPPy8gg67vNSNpuN3Nxcx3RSUhLjx48nIiKieyoUERFxUh1+d7Rx3Ekb\nioqKSEpK4pVXXiE7O/uk1g8K8sHNzbWjm+1SdntH3k7dNzl7j+qvb3P2/sD5e1R/XaPdEA4JCSEv\nL88xnZOTg91uB+Drr7+moKCAa6+9lpqaGtLT01myZAkJCQmtjldYWNEFZXee3W4l18k/o+jsPaq/\nvs3Z+wPn71H9dW7MlrR7OHrSpEmsW7cOgOTkZEJCQvDz8wPgggsu4KOPPuKtt97i+eefJy4urs0A\nFhERkZ+0+0x47NixxMXFMXv2bCwWC4sWLSIpKQmr1cqsWbN6okYRERGndFKvCd9zzz1NpkeMGNFs\nmcjISF577bWuqUpEROQUoDNmiYiImMRiGL3sGnUiIiKnCD0TFhERMYlCWERExCQKYREREZMohEVE\nREyiEBYRETGJQlhERMQkHb6AQ2+0ZMkSduzYgcViISEhgfj4eMe8VatWsXbtWlxcXBg1ahQPPvgg\ndXV1PPjgg6Snp1NfX8+9997LuHHjuO6666ioqMDHxweA++67j1GjRpnVlkNH+0tKSuKZZ54hKioK\ngIkTJ3LrrbeyZ88eHn30UQBiYmJ47LHHzGinRR3t8YUXXmDjxo0ANDQ0kJeXx7p165gxYwZhYWG4\nujZeJGTZsmWEhoaa0tPx2urv008/5YUXXsDDw4OLLrqIuXPntrrOkSNHuPfee6mvr8dut/OXv/wF\nDw8Ps9py6Ex/Tz75JN9++y11dXXcfPPNnHfeedx///0kJycTGBgIwIIFC5g2bZoZLTXR0f42b97M\n7373O4YNGwbA8OHDefjhh3vt7Qcd7/Htt99m7dq1jmV27drFtm3beu3jaEpKCrfddhs33HCD4z74\no40bN/L000/j6urKlClTWLhwIdBD+6DRx23evNm46aabDMMwjP379xtXXXWVY15paakxffp0o7a2\n1jAMw/jNb35jbNu2zVizZo2xaNEiwzAMIyUlxbjiiisMwzCMuXPnGnv37u3ZBtrRmf7eeecdY+nS\npc3Gmjt3rrFjxw7DMAzjD3/4g7Fhw4Ye6KB9nenxeElJScaKFSsMwzCM6dOnG2VlZT1U+clpq7/6\n+npjypQpRn5+vlFfX2/Mnz/fOHLkSKvr3H///cZHH31kGIZhPPXUU8aqVat6uJvmOtPfpk2bjBtv\nvNEwDMMoKCgwpk6dahiGYdx3333GZ5991uM9tKUz/X399dfGHXfc0Wys3nj7GUbnejxx/UcffdQw\njN75OFpeXm7MnTvXeOihh4zXXnut2fxf/OIXRlZWllFfX2/MmTPH2LdvX4/tg33+cPSmTZuYOXMm\nANHR0RQXF1NWVgaAu7s77u7uVFRUUFdXR2VlJQEBAVxyySU88MADQOP1kYuKikyrvz2d6a8lNTU1\nHD582PHX7fTp09m0aVPPNNGOn9NjXV0dq1evbvaXbW/SVn+FhYX4+/tjs9lwcXHh7LPPZuPGja2u\ns3nzZs4991yg99yGnenvzDPP5JlnngHA39+fyspK6uvrTeuhLZ3przW98faDn9/j3/72N2677bYe\nr/tkeXh4sGLFCkJCQprNy8jIICAggP79++Pi4sLUqVPZtGlTj+2DfT6E8/LyCAoKckzbbDZyc3MB\n8PT0ZOHChcycOZPp06czevRoBg8ejLu7O56engC8+uqr/PKXv3Ss/+yzz3LttdfyyCOPUFVV1bPN\ntKAz/QFs2bKFBQsWcP311/PDDz84dqQfBQcHO8YxW2d7BPjkk08455xz8PLycvzfokWLmDNnDsuW\nLWty/WuztNWfzWajvLycQ4cOUVtby+bNm8nLy2t1ncrKSsehr95yG3amP1dXV8fhyjVr1jBlyhTH\nSwivv/468+bN46677qKgoKDnGzpBZ/oD2L9/P7fccgtz5szhv//9L0CvvP2g8z0C7Ny5k/79+zsu\ncQu973HUzc2tyWPE8XJzc7HZbI7pH3vvqX3QKV4TPt7xD7plZWUsX76cjz/+GD8/P66//nr27Nnj\nuADFqlWrSE5O5sUXXwRg3rx5xMTEEBUVxaJFi1i1ahULFiwwpY/WnEx/o0ePxmazMW3aNLZt28Z9\n993Hyy+/3Oo4vU1HbsN33nmnyWvbd955J5MnTyYgIICFCxeybt06Lrjggh7voS3H92exWFi6dCkJ\nCQlYrVYiIyPbXaet/+sNOtLfp59+ypo1a/jHP/4BwKWXXkpgYCAjR47kpZde4vnnn+eRRx7p0frb\nczL9DRo0iNtvv51f/OIXZGRkMG/ePD755JNWx+ltOnIbrlmzhl/96leO6b7wONoZ3bUP9vlnwiEh\nIU3+KsvJyXH8RZaamsqAAQOw2Wx4eHgwbtw4du3aBcDbb7/NZ599xt///nfc3d0BmDVrluPNTDNm\nzCAlJaWHu2muM/1FR0c73swyZswYCgoKCAoKanLYPTs7u8VDM2bo7G1YUVHB0aNHmzwoXHbZZQQH\nB+Pm5saUKVN6/W0IMH78eN544w2WL1+O1WolIiKi1XV8fHwczyx6y23Ymf4AvvzyS1588UVWrFiB\n1dp4wfMJEyYwcuRIoG/sg9Byf6GhoVx44YVYLBaioqLo168f2dnZvfL2g87fhtB4iH3MmDGO6d74\nONqWE3v/8XbpqX2wz4fwpEmTWLduHQDJycmEhITg5+cHQEREBKmpqY5f2K5duxg0aBAZGRm8+eab\nPP/8847D0oZhcMMNN1BSUgI03rF+fGejmTrT34oVK/jggw+AxncE/hhgQ4YM4ZtvvgEaD+NOnjzZ\nhI6a60yPAHv27GHIkCGOcUpLS1mwYAE1NTUAbN26tdffhgA33ngj+fn5VFRUsH79eiZMmNDqOhMn\nTnT8f2+5DTvTX2lpKU8++STLly93vBMa4I477iAjIwPoG/sgtNzf2rVrWblyJdB4uDM/P5/Q0NBe\neftB53qExhDy9fV1HJ7trY+jbYmMjKSsrIzMzEzq6upYv349kyZN6rF90CmuorRs2TK++eYbLBYL\nixYt4ocffsBqtTJr1izefPNNkpKScHV1ZcyYMdx77708/fTTfPjhh4SHhzvGWLlyJZ9++ikvv/wy\n3t7ehIaGsnjxYry9vU3srFFH+zt69Cj/8z//g2EY1NXVOd5av3//fh555BEaGhoYPXq0481pvUFH\newRYt24dGzdubHI4+tVXX+W9997D09OT2NhYHn74YSwWi1ltObTV3yeffMLf/vY3LBYL8+fP55JL\nLmlxnREjRpCTk8N9991HdXU14eHhPP74444jOWbqaH+JiYk899xzTV7ff+KJJ0hPT+cvf/kL3t7e\n+Pj48PjjjxMcHGxiZ4062l9ZWRn33HMPJSUl1NbWcvvttzN16tRee/tB5+6ju3bt4q9//WuTl7s+\n+uijXvc4umvXLp544gkOHz6Mm5sboaGhzJgxg8jISGbNmsXWrVtZtmwZAOedd57j8HlP7INOEcIi\nIiJ9UZ8/HC0iItJXKYRFRERMohAWERExiUJYRETEJAphERERkyiERURETKIQFhERMYlCWERExCT/\nH/olA20CWJWkAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "jgmH3wwt1src",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "Okay, so we are doing good!
\n",
+ "\n",
+ "Now, let me just put everything here into one function so that you can tweak the hyperparameters easily!\n",
+ "\n",
+ "Or better, do it yourself!"
+ ]
+ },
+ {
+ "metadata": {
+ "id": "OZ5TY7B_4E_v",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 415
+ },
+ "outputId": "09eccd3c-828f-4841-ee11-0cd0b397bda7"
+ },
+ "cell_type": "code",
+ "source": [
+ "X = np.linspace(-50.0, 500.0, 500)\n",
+ "Y = 2 * np.linspace(-50.0, 250.0, 500) + np.random.randn(*X.shape)\n",
+ "\n",
+ "# Normalizing\n",
+ "X = X / np.max(X)\n",
+ "Y = Y / np.max(Y)\n",
+ "\n",
+ "# separating for train and test\n",
+ "train_X = X[:250]\n",
+ "train_Y = Y[:250]\n",
+ "\n",
+ "test_X = X[250:]\n",
+ "test_Y = Y[250:]\n",
+ "\n",
+ "def linear_regression(learning_rate, n_epochs, interval): \n",
+ " x1 = tf.placeholder(tf.float32, name=\"x1\")\n",
+ " y1 = tf.placeholder(tf.float32, name=\"y1\")\n",
+ "\n",
+ "\n",
+ " wght = tf.Variable(0.0, name='wght')\n",
+ " bs = tf.Variable(0.0, name='bs')\n",
+ "\n",
+ " pred_y = ((wght)*x1) + bs\n",
+ "\n",
+ " loss = tf.reduce_mean(tf.square(y1 - pred_y))\n",
+ "\n",
+ " optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)\n",
+ "\n",
+ " with tf.Session() as sess:\n",
+ "\n",
+ " sess.run(tf.global_variables_initializer())\n",
+ "\n",
+ " for epoch in range(n_epochs):\n",
+ " _, curr_loss = sess.run([optimizer, loss], feed_dict={x1:train_X, y1:train_Y})\n",
+ "\n",
+ " if epoch % interval == 0:\n",
+ " print ('Loss after epoch', epoch, ' is ', curr_loss)\n",
+ "\n",
+ " print ('Now testing the model in the test set')\n",
+ " final_preds, final_loss = sess.run([pred_y, loss], feed_dict={x1:test_X, y1:test_Y})\n",
+ "\n",
+ " print ('The final loss is: ', final_loss)\n",
+ "\n",
+ " plt.plot(test_X[:10], test_Y[:10], 'g', label='True Function')\n",
+ " plt.plot(test_X[:10], final_preds[:10], 'r', label='Predicted Function')\n",
+ " plt.legend()\n",
+ " plt.show()\n",
+ "\n",
+ "linear_regression(learning_rate=0.000005, n_epochs=100, interval=50)\n"
+ ],
+ "execution_count": 26,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.03985174\n",
+ "Loss after epoch 50 is 0.03983989\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.51966065\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeEAAAFKCAYAAAAqkecjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3Xt8VPWd//H3mVtuM0gSJ4Bc1B8g\n2CBKRAviBRW020qrqCQqsrpsERURNIuYoomVpNbbbhXb1dUiCmpcNz91H7rSauXXrg2goqBplQIW\nwjUJJCETcplMzu+PJEMCCeGS5DsZXs/HI48553vO+Z7vh+E83jnnTOZYtm3bAgAAPc5hegAAAJys\nCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAxx9fQOS0urenqXXS4xMV7l5QdMD6NLUEtkiqZapOiq\nh1oiU6TX4vf72m3nTPg4uFxO00PoMtQSmaKpFim66qGWyNRbayGEAQAwhBAGAMAQQhgAAEMIYQAA\nDCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMCQHv/uaAAAIkl9qF47Azu0PVCs7VXFcjvc\nmjr8RlmW1e37JoQBAFHtQPCAtlcVa3tgm4qrmoK2uGpb+HV39S7Zsttsc+mgy+WP93f72AhhAECv\nVllXoR27N2vDtm+0vepg0G6v2qbtgWKV1ZS1u53Tcuo070CNO+0iDfIO1mDfYA32na5z/KN7JIAl\nQhgAEMFs21ZpTamKq7Y2n7k2h2vLdKBYVfX72902xhmjQb7BSk0+R4N9QzTIN1iDfIM12DdEg31D\n1D9hgFwOszFICAMAjGlobNDu6l3aXlWsbc1BG75cHCjWjqrtqg3Vtrut1+1rPnsdouEpQ5Xs6q/B\nzUE7yDdE/ji/HFZkf/6YEAYAdJvahlrtDGxXcfg+7LbwGez2qmLtDOxQyA61u21ybLJGJJ0dPoMd\n4huiQc1ntIO9g3VKTN/wh6f8fp9KS6t6srQuQQgDAA4TagwpEKxSVX3Tz/76/QrU72+aD7fvV6B5\neVNb0/JA622C7QejJUv9EwYord/YprNXb3O4Nt+XHegbpAR3Qg9X3fMIYQCIIsFQUFXB/eHwDDSH\nZVWrQK2qr1RVfZWCjlqV7t+nqmDVwYBt/jnQUH1c+3c5XOrj6SOvp49O73OGEmMTm85kvYPb3Jcd\n6B0kj9PTxdX3PoQwABwj27bV0NigBrtBDY3BpunGUNO03dA833BwnVBTe6gxpGDz+iG7aZtgY1Ch\ncF+tf1r6CoX3UReqC59tVgWrVFW3/7Az0I7un3Ym1hkrr8cnn8enfgn95XM3Tbe0+dx9ml5j+jQv\na55vWad5eYwzpkf+vjZaEMIAIlowFFRdqFY1DbWqC9WqtqFWNaEa1TXUqjZUq9qGGtU21Kk2VKO6\n5tfW69a2vDbUtGmrD9WHwzDYHHyhxoamkLRD4emmgAwpGAo2B2dDh/cwTYh3Jcjn8alvTF8N9g2W\n19MnHKAHQ7JtWx/PKfJ6fDqj/wDVByx53T7OSg0hhAFDbNtWXahONQ0HVNNQo9qGGh1oqFGosUGJ\nwQSVl7e9HHjolwm07qfDfXS0TQftR+qv4/1LDY3Bg2HXHIY1LaHYUCNHTKP27d/fYVC2hGxTUDZt\nU9v82p2B53K45LJccjpccjlccjtcclpN0y6HS7GuWLksl1wOd3ObU7GeGCnkaN7GKbfD3Wab1n26\nm+edlktuh1suh7O53d20vdXUR7j/Q/txuOWyDm7jccYcDFd30xnoifyJjT/Rp9KG3vdhpmhCCAOH\n6CgcW+ZrGmpUE2yeDtWoJth6Wat1OtimNlSjA83bHCkMTyYxzhjFOGMV64pVrCtOyXGnKtYVp1hn\nrGJcsYprfo11xja3xzS9umIV44xVXPNrrCtWca44xbQsd8Yp1hWjWGecYlxNbS19eRye47ps2ls/\nhYvIRAgjItm2rWBjUPWhOtWF6ptf61QfqlddY53qW6ZDdeF1Ync7tLdif5u22vbCsIfD0ZKlOFe8\n4t1xinPFKyk2WQO98YprDpE4V9N0vCu+6czL4VZ8nEcHaurb7avdfRwhTLp0mw7aXU5Xc0DGNgff\nwcCMccZowKnJqqkKhYMztlXgxjhjIv5vOYHuQgijXXWhOgXqAwoEqxSoD6g6WK3aUE27odimrbFt\nW7AlKBsPCdI22zZPN7btu7t1FI4tZ1Otw7FlPhya7tbtcU1nWM3rxLfaNs4df1xnXNF2thVt9QBd\nhRCOEsFQsCkwg4FweFYHq1tNt7QfDNZAMKB61WhfdUWr5U3bBRuD3TrelvtbMU6PPM4YeZwxSnAn\nHNYW4/TI7fAc1nbYeg6PkvueovoDtjytlncUji1nYHyKE4BJRxXCeXl5Wr9+vSzLUlZWlkaPHn3Y\nOk899ZS+/PJLvfrqq10+yGgUagw1BV+r8GtvurpNmLYN0EAwoOr6pnVP5MzR5XDJ6/bK6/apf8IA\nJbi9TfMen7xurxLcCfK6fYp1xTaHXnOAOmLkcXoU0xyEB6cPaXPEHBKanm65/MjZFoDeptMQXrt2\nrbZu3ar8/Hxt3rxZWVlZys/Pb7POpk2b9Omnn8rtdnfbQNuzt2avnvrsMVXVV6nRblSj3Shbjc3T\ndritUY2yW6Zb/8iWWtZT22V2q3UObbOcUkNDqE0/7fVvt+nTbm6zFWpsOO6/5ZMkh+UIB2VSbLKG\n9DldXrdPCZ7m8GwVoIeGacIh7WeeNkD799VzRggABnQawoWFhZo0aZIkaejQoaqsrFQgEJDX6w2v\n89hjj2n+/PlasmRJ9420Hd/s+4te/Or5LuvPYTmafuQIT1uWo1W7Jcuy5HQ4Jds62N7843S45Nbh\n7ZYcsiyrTT8Jbq+8nuZgdDcHo6fpbNTbTpgmtCxzexXniuuy0Ix1xarK6t5LzwCA9nUawmVlZUpN\nTQ3PJyUlqbS0NBzCBQUFuvDCCzVw4MDuG2UHJgy8RF/ftqnp7xCtQ4IzHKRWu+2WZR0Stkcfalz2\nBAB0hWP+YFbrP+SvqKhQQUGBli5dqj179hzV9omJ8XK5nMe62w755euyvo5pv34z++0O1BKZoqkW\nKbrqoZbI1Btr6TSEU1JSVFZWFp4vKSmR3++XJK1evVr79u3TLbfcovr6em3btk15eXnKysrqsL/y\n8gNdMGyzoulMmFoiUzTVIkVXPdQSmSK9lo5+Qej0I6oTJkzQypUrJUlFRUVKSUkJX4r+wQ9+oPff\nf19vvvmmlixZotTU1CMGMAAAOKjTM+G0tDSlpqYqIyNDlmUpOztbBQUF8vl8mjx5ck+MEQCAqHRU\n94QzMzPbzI8cOfKwdQYNGsTfCAMAcAz4wlYAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQ\nBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwh\nhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABD\nCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDA\nEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEA\nMIQQBgDAEEIYAABDCGEAAAwhhAEAMIQQBgDAENfRrJSXl6f169fLsixlZWVp9OjR4WVvvvmm3nrr\nLTkcDo0cOVLZ2dmyLKvbBgwAQLTo9Ex47dq12rp1q/Lz85Wbm6vc3NzwspqaGr333ntasWKF3njj\nDW3ZskVffPFFtw4YAIBo0WkIFxYWatKkSZKkoUOHqrKyUoFAQJIUFxenZcuWye12q6amRoFAQH6/\nv3tHDABAlOj0cnRZWZlSU1PD80lJSSotLZXX6w23vfDCC3rllVc0Y8YMDR48+Ij9JSbGy+VynsCQ\nI4Pf7zM9hC5DLZEpmmqRoqseaolMvbGWo7on3Jpt24e1zZo1SzNmzNBPf/pTnX/++Tr//PM73L68\n/MCx7jLi+P0+lZZWmR5Gl6CWyBRNtUjRVQ+1RKZIr6WjXxA6vRydkpKisrKy8HxJSUn4knNFRYU+\n/fRTSVJsbKwuvfRSrVu3rivGCwBA1Os0hCdMmKCVK1dKkoqKipSSkhK+FN3Q0KCFCxequrpakvTV\nV1/pzDPP7MbhAgAQPTq9HJ2WlqbU1FRlZGTIsixlZ2eroKBAPp9PkydP1t13360ZM2bI5XJpxIgR\nuvLKK3ti3AAA9HpHdU84MzOzzfzIkSPD01OnTtXUqVO7dlQAAJwE+MYsAAAMIYQBADCEEAYAwBBC\nGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCE\nEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAM\nIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAA\nQwhhAAAMcZkeAACgZz377L/q22//qsrKclVXH9Bppw1Unz6nKC/viS7p/4YbpiglpZ8cjoPneUuW\nvHDC/f7v//4/ff/7F2n//kq99NLzWrDgZyfcp2mEMACcZO65Z74k6U9/+r3Wry/SnDnzunwfTz75\njOLj47u0zzfeWKG0tAuUnHxqVASwRAgDAJqtW/eZ3nhjuQ4cOKA5c+br/vvn6L33PpIkLVq0QFOn\nTtPIkWcrL+8RVVVVKRQKad68f9GwYcOPqv8f/ejKw/r74ovPVV0d0LZtW7Vjx3bNnXu/xo+foA8+\neE9vvZUvy7KUkXGLgsGg/vKXr5WZOVcLFz6kRx5ZpJdeelXr1n2mF174teLiYtS3b7IefPBhffjh\nSm3Y8KUqKsq1bdtW3Xzzrbrmmmu77d/tRBDCAGBQzp8X6b83v92lfU4Zeq1yLlp8XNtu3rxJr79e\nII/H0+7yN998Xd///kWaMuVafffdFv3qV0/q3/7t1ycyXJWU7NGTTz6j1av/rHfe+S+de+55evnl\nF7Vs2euqrw8qNzdbjz32tF588d/15JPPqLKyIrztk0/+Qv/6r89p1KjhevDBRfr97z+QZVnavHmT\n/v3ff6vt24uVnZ1FCAMAIt+wYcM7DGBJ+uqrDaqoKNfKle9LkurqattdLzNzbviecN++iVq8+Jcd\n9jl69HmSpJSUFAUCAf39799pyJAzFBMTq5iYWD322NPtbrd/f6Usy1K/fv0lSWlpY/Xll+t01lkj\nNWrUaDmdTvn9KaquDnReuCGEMAAYlHPR4uM+a+0Obre73faGhobm5S7Nn/8vGjVq9BH76eyecEt/\nkuR0OsPTtm3L4XDKthuPYrSWbNsOzwWDQVmWo90+IxV/ogQAaJdlWaqtrVVtba02bvxWkvS9743S\nH/+4SpL03Xdb9MYby0+ov/acfvoZ2rZtqw4cOKC6ujrNm3eXbNuWZTkUCoXC6/Xp00eWZWn37t2S\npC+/XKeRI88+jkrN4UwYANCua6+9QbNm/aPOOOP/aMSIpnC74YZ05ebm6K67/lmNjY2aNy/zhPpr\nT1xcnGbOnK158+6SJKWn3yzLsjRmTJruumumfvaznPC6CxYs0iOP/ExxcTHy+/vryiuv0u9+9z/H\nV7ABlt3D5+mlpVU9ubtu4ff7oqIOiVoiVTTVIkVXPdQSmSK9Fr/f1247l6MBADCEEAYAwBBCGAAA\nQwhhAAAMIYQBADCEEAYAwBD+ThgATjK7du3UjBkZOuecUaqvb1B9fb1uueUfddlllx9zX//1X/mq\nqKjQpZdO1B//uEozZ97R7notjyHs6Bu5WtuyZZOefvrxwx5/eNll39c555wbnk9OTtYjj/zimMd8\nqI8//lCXXz5Jf/vbt0esoTsQwgBwEhoy5HS9+uqrKi2t0v79lbr99ls0btx4xcTEHld/w4eP0PDh\nIzpc3vIYwqMJ4Y54vd4ueS7xoZYvX6bLL5/UaQ3d4ahCOC8vT+vXr5dlWcrKytLo0Qe/M3T16tV6\n+umn5XA4dOaZZyo3N7fNg5wBAJGtT59TlJx8qvbu3aulS/9DLpdb+/dX6Oc/f0yPP56rnTt3qKGh\nQf/8z7N1/vkX6LPP1uqZZ55SUlKykpNP1WmnDdS6dZ+poOBNLV78+BEfQ/irX/1G7777f/Xhhx/I\nshy65JKJuumm6Sop2aOHHloot9utYcPOOuqx79q1U4sWPaB33216EtXMmbdq8eJf6re/fUGnnurX\nt9/+VXv27NbDDy/WiBEjtWLFMq1a9ZEsy6HZs+fom2/+ok2bNior6190ww3p4Ro++uj3ys9fIafT\nqREjzta8eZl66aXn233s4onoNITXrl2rrVu3Kj8/X5s3b1ZWVpby8/PDyx9++GG98sor6t+/v+bO\nnas//elPuuyyy05oUABwskjIWaSY/+7aRxnWTblW1TlH/1CIXbt2av/+SqWk9JPU9J3MDzzwM33w\nwXtKTj5VDz74sCoqKnTvvbO1bNkbev75JXrooUc1fPhZysycq9NOGxju68CB6iM+hrC0tESrVn2k\nX//6JUnSnXfO1OWXT1JBQb6uvPIqTZt2k5Yvf1mbNm084X+H+vp6Pf30Er399lv64IP3FB8fr1Wr\nPtLzz7+snTt3aPnyl7Vw4UNasWKZ8vKe0Lp1nzXXcEAvvPCcli59TfHx8VqwYH542aGPXez2EC4s\nLNSkSZMkSUOHDlVlZaUCgYC8Xq8kqaCgIDydlJSk8vLyExoQAKD7bdu2Vbfeeqvq6xvk8Xi0aNEj\ncrmaIuF730uVJH399QatX/+FNmz4UpJUV1enYDCoXbt2afjwprPV885LU11dXbjfzh5D+Ne/Fmn7\n9mLdc0/TfdcDB6q1e/dO/f3v3+nyy5uyZsyYsVq9+s+HjTkQCGjOnFnh+aFDhykjY3qHNZ577hhJ\nkt/fT3/5S5E2bvxW3/veKDkcDg0aNFgLFz7U7nbFxds0aNCQ8FOgxow5Xxs3fiPp8McunqhOQ7is\nrEypqanh+aSkJJWWloaDt+W1pKREn3zyie69994THhQAnCyqcxYf01lrV2l9T/hQLpc7/Dpjxj9p\n8uQftFne+pbjoY8f6OwxhC6XW+PHT9CCBT9r075ixbLwYwg72r69e8K7d+9qM3+kRyQ6nQ41Nnb+\nuATLaltXQ0NQMTEx7fZ5oo75g1nt7XTv3r2aPXu2srOzlZiYeMTtExPj5XI5j7hOb9DRl3H3RtQS\nmaKpFim66unttdTVJcjlagq8Q2uJjXXrlFPi5Pf7NG7cWP3hD3/QzTffqL1792rZsmW67777NGBA\nf1VVlerMM89UUdF6nXfeeerbN14xMW6df/4o/fznxYqPd8jlcmn27Nn67W9/K5fLqcTEOF100Vj9\nx388J6/XpdjYWOXm5iozM1MjRgzXjh1bdMklF+rbb7+Sx+M6bGyWZR3W5vE0qrKyvDmbarVr1w4l\nJSW0qeOUU+IUG+vW+PFjtXz5UiUmxqmiokLZ2dl67rnnwv8OLTWMGZOqXbu2Ky7OktfrVVHRet15\n550qLCyU1xsrv9+n8vKEdsd4rDoN4ZSUFJWVlYXnS0pK5Pf7w/OBQEA//elPNW/ePF188cWd7rC8\n/MBxDjVyRPrTOo4FtUSmaKpFiq56oqGWffuq1dDQdLZ5aC21tUFVVtaotLRKY8derFWr/qTrr79R\noVBI//RPs1RaWqXbb79Dd989R/37D1BSUrKqq+tUUXFAdXVBVVeHdNttszR9+gxJTY8hLCsLaPTo\nMZo2LV3PPvuCpk5NV3r6TXI4HLr00omqqgrqmmuu10MPLdR77/2Phg4drvr6hsPGZtt2O//2DqWl\nXaDrr79eZ5wxVMOGnaV9+6rb1FFZWaPa2qBiYk7RlVf+QOnpN8m2bd1xx90qLa3SsGFn6dprr9Od\nd84N1zB79j267bbbZVkOjR59nk4/fYQ+/HCV3O5alZZWqby8ut0xdqSjsO70UYbr1q3Ts88+q6VL\nl6qoqEiLFy/W66+/Hl6+aNEiXXDBBfrJT35yVAPp7f95peg4CFtQS2SKplqk6KqHWiJTpNfSUQh3\neiaclpam1NRUZWRkyLIsZWdnq6CgQD6fTxdffLHefvttbd26VW+99ZYk6ZprrlF6enrXjh4AgCh0\nVPeEMzMz28yPHDkyPP3111937YgAADhJ8K0aAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAI\nIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAY\nQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAA\nhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwA\ngCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggD\nAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCFHFcJ5eXlKT09XRkaGNmzY0GZZXV2dHnjgAU2d\nOrVbBggAQLTqNITXrl2rrVu3Kj8/X7m5ucrNzW2z/PHHH9fZZ5/dbQMEACBadRrChYWFmjRpkiRp\n6NChqqysVCAQCC+fP39+eDkAADh6nYZwWVmZEhMTw/NJSUkqLS0Nz3u93u4ZGQAAUc51rBvYtn1C\nO0xMjJfL5TyhPiKB3+8zPYQuQy2RKZpqkaKrHmqJTL2xlk5DOCUlRWVlZeH5kpIS+f3+495hefmB\n4942Uvj9PpWWVpkeRpeglsgUTbVI0VUPtUSmSK+lo18QOr0cPWHCBK1cuVKSVFRUpJSUFC5BAwDQ\nBTo9E05LS1NqaqoyMjJkWZays7NVUFAgn8+nyZMna+7cudq9e7e+++473XrrrZo2bZqmTJnSE2MH\nAKBXO6p7wpmZmW3mR44cGZ5+5plnunZEAACcJPjGLAAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGE\nAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMI\nYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQ\nQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAw\nhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAA\nDCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMCQowrhvLw8paenKyMjQxs2bGiz7M9//rNu\nuOEGpaen67nnnuuWQQIAEI06DeG1a9dq69atys/PV25urnJzc9ssX7x4sZ599lm9/vrr+uSTT7Rp\n06ZuGywAANHE1dkKhYWFmjRpkiRp6NChqqysVCAQkNfrVXFxsU455RQNGDBAknTZZZepsLBQw4YN\n695RN0vIWaSY/367R/bVhsNSUqPd8/vtDtQSmaKpFim66qGWyNSFtdRNuVbVOYu7pK/OdBrCZWVl\nSk1NDc8nJSWptLRUXq9XpaWlSkpKarOsuLj4iP0lJsbL5XKewJBbifdIDqtr+jpGTkP77Q7UEpmi\nqRYpuuqhlsjUVbXEx3sU7/d1SV+d6TSED2XbJ/abRnn5gRPavo0FDzf99DC/36fS0qoe3293oJbI\nFE21SNFVD7VEpi6vpYv/XfwdhHqn94RTUlJUVlYWni8pKZHf72932Z49e5SSknKiYwUA4KTQaQhP\nmDBBK1eulCQVFRUpJSVFXq9XkjRo0CAFAgFt375dDQ0N+vjjjzVhwoTuHTEAAFGi08vRaWlpSk1N\nVUZGhizLUnZ2tgoKCuTz+TR58mTl5OTo/vvvlyT98Ic/1JlnntntgwYAIBoc1T3hzMzMNvMjR44M\nT19wwQXKz8/v2lEBAHAS4BuzAAAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAA\nDLHsE30iAwAAOC6cCQMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIUf1POFolZeXp/Xr18uy\nLGVlZWn06NGHrfPUU0/pyy+/1Kuvvqo1a9bo3nvv1fDhwyVJZ511lh566CHt2rVLDz74oBoaGuRy\nufTEE0/I7/crNTVVaWlp4b5efvllOZ3OiK5l4cKFKioqUt++fSVJM2fO1MSJE/Xuu+9q2bJlcjgc\nmjZtmm688cZuqaMra5k7d67Ky8slSRUVFTrvvPN0xx13aMqUKRo1apQkKTExUc8880zE1CJJ7777\nrl588UW5XC7NnTtXEydO1K5du7RgwQKFQiH5/X498cQT8ng8Pfq+dHU9ve2Y6aiW3njMdFRLbzxm\n/vM//1PvvvtueNnXX3+tL774Qt98841ycnIkSSNGjNAjjzwiSXrxxRf1wQcfyLIszZkzR5dddlm3\n1XJU7JPUmjVr7FmzZtm2bdubNm2yp02bdtg6f/vb3+z09HR7+vTptm3b9urVq+177rnnsPUWLFhg\nv/fee7Zt2/by5cvtX/7yl7Zt2/aFF17YXcNvoytreeCBB+w//OEPbdqqq6vtq666yt6/f79dU1Nj\n/+hHP7LLy8u7oZKuraW1hQsX2uvXr7eLi4vt6667rusH3o7jqWXfvn32VVddZVdVVdl79uyxFy1a\nFB7/+++/b9u2bT/11FP2ihUrevR96ep6euMx01EtvfGY6aiW1nrLMXPo9jk5ObZt2/b06dPt9evX\n27Zt2/fdd5+9atUqe9u2bfZ1111n19XV2Xv37rWvvvpqu6GhoRsr6txJezm6sLBQkyZNkiQNHTpU\nlZWVCgQCbdZ57LHHNH/+/E54LU3WAAAFuklEQVT7ys7O1tVXXy2p6bfEioqKrh/wEXRlLe1Zv369\nzjnnHPl8PsXGxiotLU3r1q074XG3pztq2bJli6qqqtr9jbo7HU8thYWFGj9+vLxer1JSUvToo49K\nktasWaMrr7xSknT55ZersLCwR9+Xrq6nNx4zHdXSnkg/ZjqrpTcdM60999xzuuuuu1RfX68dO3aE\nx99yzKxZs0aXXHKJPB6PkpKSNHDgQG3atKl7i+rESRvCZWVlSkxMDM8nJSWptLQ0PF9QUKALL7xQ\nAwcObLPdpk2bNHv2bN1000365JNPJEnx8fFyOp0KhUJ67bXXNGXKFElSfX297r//fmVkZGjp0qW9\nohZJWr58uWbMmKH58+dr3759KisrU1JSUof9R3ItkvTKK69o+vTpbfYxd+5cZWRktLmM1dWOp5bt\n27ertrZWs2fP1s0336zCwkJJUk1NjTwejyQpOTlZpaWlPfq+dHU9vfGY6agWqfcdM0eqRepdx0yL\nDRs2aMCAAfL7/SovL1efPn3Cy0wdM0fjpL4n3Jrd6ts7KyoqVFBQoKVLl2rPnj3h9jPOOENz5szR\nP/zDP6i4uFgzZszQ7373O3k8HoVCIS1YsEDjxo3T+PHjJUkLFizQj3/8Y1mWpenTp2vs2LE655xz\nIrqWn/zkJ+rbt6/OPvtsvfDCC1qyZInGjBnTYf+RXIvH41F9fb0+//zz8L2hvn376t5779WPf/xj\nVVVV6cYbb9S4ceOUkpISEbW0LFuyZIl27typGTNm6OOPP+6wn6Np7y4nUo9lWb3umOmolt54zLQs\na+996Y3HjCS99dZbuu666zrt52jae9JJeyackpKisrKy8HxJSYn8fr8kafXq1dq3b59uueUWzZkz\nR0VFRcrLy1O/fv30wx/+UJZlaciQITr11FPD/xkefPBBnX766ZozZ064z5tuukkJCQmKj4/XuHHj\ntHHjxoivZfz48Tr77LMlSVdccYU2btzYbv/ddQB29fvy6aeftrmk5vV6df3118vtdispKUmjRo3S\nli1bIqaW5ORkjRkzRi6XS0OGDFFCQoL27dun+Ph41dbWSpL27NmjlJSUHn1furoeqfcdMx3V0huP\nmSO9L73tmGmxZs2a8C8/SUlJbW5xdHTMtLQbZeJGdCT4/PPP7dtuu822bdv++uuv7YyMjHbXKy4u\nDn8A4J133rFffPFF27Ztu6SkxJ44caJdV1dnv/POO3ZWVlab7TZv3mzfd999dmNjox0MBu309PTw\nhwQiuZY5c+bY27Zts2276QMzOTk5dk1NjT1p0iS7srLSDgQC4Q+cRHottm3bv/nNb+xXXnklvF1h\nYaGdl5dn2/bBD8/s3r07YmrZvXu3fdttt9mhUMjet2+fPXHiRDsUCtmLFi2y3377bdu2bfvRRx+1\n33zzzR59X7q6nt54zHRUS288ZjqqxbZ73zHTUs+hHx67/fbb7U8//dS2bduePXu2/cknn9g7duyw\nr7nmGruurs7evXu3fdVVV4XrNuWkvRydlpam1NRUZWRkyLIsZWdnq6CgQD6fT5MnT253myuuuEKZ\nmZn66KOPFAwGlZOTI4/Ho9dee011dXW69dZbJTV9oCAnJ0f9+/fXDTfcIIfDoSuuuKLbPuTQlbXc\ncsstmjdvnuLi4hQfH69f/OIXio2N1f3336+ZM2fKsizdfffd8vl8EV+LJJWWlmrIkCHhdceOHau3\n335b6enpCoVCmjVrlvr16xcxtfTr109XX321pk2bJklatGiRHA6H7rnnHj3wwAPKz8/Xaaedpmuv\nvVZut7vH3peurqc3HjMd1dIbj5mOapF63zHTMubW93olKSsrSw8//LAaGxt17rnn6qKLLpIkTZs2\nTdOnT5dlWcrJyQnXbQqPMgQAwJCT9p4wAACmEcIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMA\nYAghDACAIf8fS9tNmaMjqL8AAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "A6MaclhK4rc6",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 551
+ },
+ "outputId": "b1e15e78-8771-4fc1-84ba-a0f121a602af"
+ },
+ "cell_type": "code",
+ "source": [
+ "# Okay! Now let's tweak!\n",
+ "linear_regression(learning_rate=0.000034, n_epochs=500,interval=50)"
+ ],
+ "execution_count": 27,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.03985174\n",
+ "Loss after epoch 50 is 0.039771408\n",
+ "Loss after epoch 100 is 0.0396916\n",
+ "Loss after epoch 150 is 0.039612323\n",
+ "Loss after epoch 200 is 0.03953356\n",
+ "Loss after epoch 250 is 0.039455317\n",
+ "Loss after epoch 300 is 0.039377593\n",
+ "Loss after epoch 350 is 0.039300375\n",
+ "Loss after epoch 400 is 0.03922366\n",
+ "Loss after epoch 450 is 0.039147448\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.5136106\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeEAAAFKCAYAAAAqkecjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3Xl8VPW9//H3mS0LM4EEZkCWqBeR\nJYgaV0QFNai3lV5XiBWpvdSligiKCClKvEpq3W7rpe3Vn15FwRqvNz/1/vQnbb36a2sDWNGouCBo\nWWRJAknIZJlkJuf3R5IhgYREmOQ7GV7PxyOPOev3fD8ZDu/5zpnMsWzbtgUAAHqdw3QHAAA4WhHC\nAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAY4urtA5aVVff2IWMuPT1VFRW1prsRE9QSnxKpFimx6qGW\n+BTvtfj9vg6XMxI+DC6X03QXYoZa4lMi1SIlVj3UEp/6ai2EMAAAhhDCAAAYQggDAGAIIQwAgCGE\nMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAY0uvfHQ0AQDxpjDRqR8232l69Tduqt8rtcOvK\nUdfIsqwePzYhDABIaPXheu0IbtfW6q0tQbtF21oCd3v1Nu2s2aEmu6ndPucPv0D+VH+P940QBgD0\naTWNNSor26aSLZ9pW/W2g4K2tHZ3h/s5LIeG9humM4ecrRG+TI3wjdBwX6Ym+E/ulQCWCGEAQJzb\nF6o6aBS7PTqS3ao99Xs63M/tcGuod5jOGzZZw30jNNw3oiVsm3+O6TdUbqe7l6tpjxAGABhj27b2\n1u/V9uqt7YK2+bE5aPc1VHW4b7IzWcN9I3SS/2SN8o+U331MS9AeqxG+ERqcOkROR3zf4pAQBgD0\nmCa7SWW1pdHrr1tbRq/booG7TbXhmg73TXX1U2Zaps70nqURaZka7stUpi8zGrT+FH/0w1N+v09l\nZdW9WVpMEMIAgA5FmiKqaQxqX8M+VTdUq7qhWsHG5un9y/Yp2LKuedk+BRv3z1fU71UoEuqw/f5J\nA3R8/3/QiLRMjfCOaA5ab/O12RFpmUpPyuiVTyibRAgDQIKJNEWiQbj/p6r5Mbp8n8LOepVW7dkf\npo3V2hfaF92mpjF4WMd3O9xK86TJ6/FpbMY4DY9ehx3RbjotqX+MK+97CGEAiIFIU0RhO6xwU1jh\npkaFW+cjjS3LW5a1rrfDLfONCjeFFbHDamxq3j/SFFZjdHkkOh2KhLSvoSo68mwNz+rWUWmMwtPn\nSZO/f0A+j08+j09et09pSWnyudOa51uWp3n679/G45PPnaa0pDQlOZNi/NtNXIQwgD7Btm3VR+pV\nH65TKBJSXbhO9eF6hSL1qg/Xq65leX24TvWR1vnmdc3LWtaF61UfqVdDpEFhe3/gRZoibYKvORAj\nLaHY2NSoiN0coBGF1RhuVNjeH6DhprBs2cZ+Nx6HR2lJafK6fe3C0+dpDs224dkasj6PT5mDhyhc\n44zOE569jxAG4kC4Kaz6cJ1qw3WKNIXVkOTVnmD70Uxn/8nbduf/+Xe6zyECo7P2DnX8cFNYdZE6\nhVoCrjnsQqqPNIeeO0Uqq6yMBmh9uE514XrVR+oUatmurk2gtgZpfZv2OruuGGsuh0tuh1tOyyWX\nwymXwy2XwyWX5VKSM0lJbp8s29G83HLK2bK9y+GKbtc87ZbL4ZTTcsntdMtluVq2bX50WS3HcTgP\necxouw6XkpzJLSPQtJbR6JGFZ1/9MFMiIYSBQ2iym1QXrmv5qVVdY8tjuE61LY/1bde3Lm+zXdt1\ndeFa1bZZVx+pV11jrRqaGkyXGhcsWUpxpSjZlawkZ7JS3anKSB6oZFeSkl0pSnYmtzy2zLdsl+JK\nVrIzRUmuZCW7kpXiTFGSK0nJzuZtUlwpSmqzT7IzWR5n0kGB6LAcXX4QiOBCLBHC6BNaR1uhppAa\nIiE1RBoUavcYUmqtS7v3VKghElIo0qCGplDL25S1qg3Xqa6x9qBArGsZfdZ3ErT1kfqY1uFxeJTi\nTlWKK0Wp7lQNTBnUPO1KbQmfFLkcLiUnu1Vf33jQ/pY6DohDBUdv7ON2uJXsTG4OwQ6CMpCeroZa\nW8mulHahmexq3ielZR+3w53wn4YF2iKEcUitf6JQ01ijukidGiINLSHXPgjbLeskKEMt1+E63CcS\nUkPTodvuyWtuTsupVHc/pbhSlOJKUf+kY1qmU1tGUqnR+RR3ilJbpw94THUfvDzZ1bx9a8B2R6KN\nthKtHiBWCOEEY9u26sJ1CjYGFWysVk1DUMHGYMufHwQVbJkPNlQr2BhUxBlS+b69Ldu3rq9WsCGo\nmsagasO1vdJvp+VUkjNJHqdHHmeSkpxJ6p/UX0nOZCW1LPM4k5TkaF3fZlnLdLrPp3BI7bZLdiVH\nR5mtI9DWcExtE5amv7oOwNGpWyFcUFCgkpISWZalvLw8TZgw4aBtHnvsMX300Ud64YUXYt7JRNcQ\naYgGX9sgrDkgFFuDdf90UDUtYdp2/YF3A/kuUl395PV45fP4dIx3qLxub/OPx6tkZ4o8Tk9LWCa1\nm46GoqODZW2mOw7UpJh8tRyjLQB9TZchvG7dOm3ZskWFhYXavHmz8vLyVFhY2G6bTZs26f3335fb\n3bujiZrGGv3u8xe0r2GfbNlqspvUZDfJtpvUZLfMq+mA5W2X2Z0sb2oJMrvddq3buN0O1Yca2m3b\nJHt/O21+7AOPJVuRprBqwrXRAD2ST316HB55PV553T4N8w6PBqjX7YuGp9ftVT+Pr02g7p/OHDJE\nDdWWvB6vUl394v57VgEgkXQZwsXFxcrJyZEkjRw5UlVVVQoGg/J6vdFtHnroIc2fP1/Lly/vuZ52\nYO3OYuX9ZWGvHrM7LFlyWI7oT+u81WZZP1c/DUwZpGPTjjsgIL0HBKhPXo9X/dz7p9uu8zg9R9RX\n/yCfymxGjwBgQpchXF5erqysrOh8RkaGysrKoiFcVFSkM888U8OGDeu5XnZiyogL9X+u+INqwzX7\nQ0+ONoFntVt2YBDuX25Flx8UoAds57AcCvj7a8+emnbttg1cPt0JAOiO7/zBrLZ/yF9ZWamioiI9\n++yz2r2745smHyg9PVUuV+ze8vx+ICdmbX0XaUPTjBy3J/j9PtNdiBlqiV+JVA+1xKe+WEuXIRwI\nBFReXh6dLy0tld/vlyStWbNGe/fu1XXXXaeGhgZt3bpVBQUFysvL67S9iore+bRtT0qkDwBRS3xK\npFqkxKqHWuJTvNfS2QsER1c7Tpo0SatXr5YkbdiwQYFAIPpW9KWXXqo333xTL7/8spYvX66srKxD\nBjAAANivy5Fwdna2srKylJubK8uytHTpUhUVFcnn82nq1Km90UcAABJSt64JL1iwoN38mDFjDtpm\n+PDh/I0wAADfQZdvRwMAgJ5BCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIA\nABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQw\nAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAgh\nDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhC\nCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACG\nEMIAABhCCAMAYAghDACAIa7ubFRQUKCSkhJZlqW8vDxNmDAhuu7ll1/WK6+8IofDoTFjxmjp0qWy\nLKvHOgwAQKLociS8bt06bdmyRYWFhVq2bJmWLVsWXVdXV6c33nhDq1at0ksvvaSvv/5aH374YY92\nGACARNFlCBcXFysnJ0eSNHLkSFVVVSkYDEqSUlJStGLFCrndbtXV1SkYDMrv9/dsjwEASBBdhnB5\nebnS09Oj8xkZGSorK2u3zVNPPaWpU6fq0ksv1YgRI2LfSwAAElC3rgm3Zdv2QctuuukmzZo1Szfe\neKNOO+00nXbaaZ3un56eKpfL+V0PG3f8fp/pLsQMtcSnRKpFSqx6qCU+9cVaugzhQCCg8vLy6Hxp\naWn0LefKykp99dVXOuOMM5ScnKzzzz9f69evP2QIV1TUxqDbZvn9PpWVVZvuRkxQS3xKpFqkxKqH\nWuJTvNfS2QuELt+OnjRpklavXi1J2rBhgwKBgLxeryQpHA5r0aJFqqmpkSR98sknOv7442PVZwAA\nElqXI+Hs7GxlZWUpNzdXlmVp6dKlKioqks/n09SpU3Xbbbdp1qxZcrlcGj16tC666KLe6DcAAH1e\nt64JL1iwoN38mDFjotNXXnmlrrzyytj2CgCAowDfmAUAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGE\nMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAI\nIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAY\nQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCEu0x0A\nAPSuf/u3f9WXX36uqqoK1dTUaujQYUpL66+Cgkdi0v7VV09TIDBYDsf+cd7y5U8dcbt/+cv/01ln\nnaN9+6r0zDNPauHCnx1xm6YRwgBwlLn99vmSpD//+Q8qKdmgOXPmxfwYjz76hFJTU2Pa5ksvrVJ2\n9hkaOHBQQgSwRAgDAFqsX/83vfTSStXW1mrOnPm66645euONtyVJS5Ys1JVXTteYMWNVUHC/qqur\nFYlENG/e3TrhhFHdav/737/ooPY+/PAD1dQEtXXrFn377XbNnXuXJk6cpLfeekOvvFIoy7KUm3ud\nGhsb9dlnn2rBgrlatOhe3X//Ej3zzAtav/5veuqp3yglJUkDBgzU4sX36Y9/XK2PP/5IlZUV2rp1\ni374w+t12WWX99jv7UgQwgBgUP5fl+i/N78a0zanjbxc+ec8eFj7bt68Sb/7XZE8Hk+H619++Xc6\n66xzNG3a5frmm6/1q189ql/+8jdH0l2Vlu7Wo48+oTVr/qrXXvsvnXzyKXruuae1YsXv1NDQqGXL\nluqhhx7X00//ux599AlVVVVG93300Z/rX//11xo/fpQWL16iP/zhLVmWpc2bN+nf//0/tH37Ni1d\nmkcIAwDi3wknjOo0gCXpk08+VmVlhVavflOSFArVd7jdggVzo9eEBwxI14MP/qLTNidMOEWSFAgE\nFAwG9fe/f6PMzOOUlJSspKRkPfTQ4x3ut29flSzL0uDBQyRJ2dmn66OP1uvEE8do/PgJcjqd8vsD\nqqkJdl24IYQwABiUf86Dhz1q7Qlut7vD5eFwuGW9S/Pn363x4yccsp2urgm3tidJTqczOm3bthwO\np2y7qRu9tWTbdnSusbFRluXosM14xZ8oAQA6ZFmW6uvrVV9fr40bv5QkjRs3Xn/607uSpG+++Vov\nvbTyiNrryLHHHqetW7eotrZWoVBI8+bdKtu2ZVkORSKR6HZpaWmyLEu7du2SJH300XqNGTP2MCo1\nh5EwAKBDl19+tW666Uc67rh/0OjRzeF29dUztGxZvm699SdqamrSvHkLjqi9jqSkpGj27Fs0b96t\nkqQZM34oy7J06qnZuvXW2frZz/Kj2y5cuET33/8zpaQkye8foosuuli///3/PbyCDbDsXh6nl5VV\n9+bheoTf70uIOiRqiVeJVIuUWPVQS3yK91r8fl+Hy3k7GgAAQwhhAAAMIYQBADCEEAYAwBBCGAAA\nQwhhAAAM4e+EAeAos3PnDs2alauTThqvhoawGhoadN11P9LkyRd857b+678KVVlZqfPPn6I//eld\nzZ59c4fbtd6GsLNv5Grr66836fHHHz7o9oeTJ5+lk046OTo/cOBA3X//z79znw/0zjt/1AUX5Oir\nr748ZA09gRAGgKNQZuaxeuGFF1RWVq19+6r04x9fp7PPnqikpOTDam/UqNEaNWp0p+tbb0PYnRDu\njNfrjcl9iQ+0cuUKXXBBTpc19ARCGACOcmlp/TVw4CDt2bNHzz77v+RyubVvX6X+5V8e0sMPL9OO\nHd8qHA7rJz+5Raeddob+9rd1euKJx5SRMVADBw7S0KHDtH7931RU9LIefPDhQ96G8Fe/+q1ef/1/\n649/fEuW5dB5503RtdfOVGnpbt177yK53W6dcMKJ3e77zp07tGTJPXr99eY7Uc2efb0efPAX+o//\neEqDBvn15Zefa/fuXbrvvgc1evQYrVq1Qu+++7Ysy6FbbpmjL774TJs2bVRe3t26+uoZ0RrefvsP\nKixcJafTqdGjx2revAV65pknO7zt4pEghAHAoH75S5T037G9lWFo2uWqye/+TSF27tyhffuqFAgM\nltT8ncz33PMzvfXWGxo4cJAWL75PlZWVuuOOW7RixUt68snluvfeBzRq1IlasGCuhg4dFm2rtrbm\nkLchLCsr1bvvvq3f/OYZSdJPfzpbF1yQo6KiQl100cWaPv1arVz5nDZt2njEv4eGhgY9/vhyvfrq\nK3rrrTeUmpqqd999W08++Zx27PhWK1c+p0WL7tWqVStUUPCI1q//W0sNtXrqqV/r2WdfVGpqqhYu\nnB9dd+BtF3slhAsKClRSUiLLspSXl6cJE/bfPWPNmjV6/PHH5XA4dPzxx2vZsmXR21cBAOLT1q1b\ndP3116uhISyPx6MlS+6Xy9UcCePGZUmSPv30Y5WUfKiPP/5IkhQKhdTY2KidO3dq1Kjm0eopp2Qr\nFApF2+3qNoSff75B27dv0+23N193ra2t0a5dO/T3v3+jCy7IkSSdeurpWrPmrwf1ORgMas6cm6Lz\nI0eeoNzcmZ3WePLJp0qS/P7B+uyzDdq48UuNGzdeDodDw4eP0KJF93a437ZtWzV8eGb0LlCnnnqa\nNm78QtLBt108Ul2G8Lp167RlyxYVFhZq8+bNysvLU2FhYXT9fffdp+eff15DhgzR3Llz9ec//1mT\nJ08+4o4BwNGgJv/B7zRqjZW214QP5HK5o4+zZv2zpk69tN36tgOtA28/0NVtCF0utyZOnKSFC3/W\nbvmqVSuityHsbP+Orgnv2rWz3fyhbpHodDrU1NT17RIsq31d4XCjkpKSOmzzSHU5ZC0uLlZOTvOr\nk5EjR6qqqqpd+hcVFWnIkOYbKmdkZKiiouKIOwUAMG/cuPH6y1/+nySpomKvnnzy15KkQYP82rr1\n77JtWx9++EG7fbq6DeHo0WO1fv0Hqq+vl23b+uUvH1UoVK/MzGP1xRefSVL0rd/uSE3tp4qKvbJt\nW3v2lGvHju2dbjt69Fh98kmJwuGw9u7do8WLm+8AdWAwjxhxrLZv36ra2hpJ0ocfrtfo0eO63afv\nosuRcHl5ubKysqLzGRkZKisrk9frlaToY2lpqd577z3dcccdh2wvPT1VLpfzkNv0BZ3dEaMvopb4\nlEi1SIlVT1+vJRTqJ5ereQx2YC3JyW71758iv9+nGTOu0GeffaTbb79RkUhEc+bMkd/v091336X8\n/DwNHTpUmZnD1a9fkgYMSFVSkluZmQHNnz9Pd999uyTphhtuUCCQpokTz9LcuTfp+eef1z//8w26\n446b5XQ6lZOTo+HD/br55p9o3rx5WrPmzzrxxBPl8bgO6ptlWQct8/t9OvfcSbrqqqs0ZswYjRs3\nThkZ/drV0b9/ipKT3ZowYbSuuuoKzZ//U9m2rfnz58vv9ykra5x++tMf6+67747WsHjxIt1zzzw5\nHA6ddtppysk5T59//pG83mT5/T5VVPTrsI/fVZe3Mrz33ns1efLk6Gj42muvVUFBgY4//vjoNnv2\n7NGNN96oO++8U+eee+4hDxjPt5rqrni/ZdZ3QS3xKZFqkRKrHmqJT/Fey2HfyjAQCKi8vDw6X1pa\nKr/fH50PBoO68cYbNW/evC4DGAAA7NdlCE+aNEmrV6+WJG3YsEGBQCD6FrQkPfTQQ/rRj36k888/\nv+d6CQBAAurymnB2draysrKUm5sry7K0dOlSFRUVyefz6dxzz9Wrr76qLVu26JVXXpEkXXbZZZox\nY0aPdxwAgL6uW38nvGDBgnbzY8aMiU5/+umnse0RAABHCb5VAwAAQwhhAAAMIYQBADCEEAYAwBBC\nGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCE\nEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAM\nIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAA\nQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYA\nwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCkWyFcUFCgGTNmKDc3Vx9//HG7\ndaFQSPfcc4+uvPLKHukgAACJqssQXrdunbZs2aLCwkItW7ZMy5Yta7f+4Ycf1tixY3usgwAAJKou\nQ7i4uFg5OTmSpJEjR6qqqkrBYDC6fv78+dH1AACg+7oM4fLycqWnp0fnMzIyVFZWFp33er090zMA\nABKc67vuYNv2ER0wPT1VLpfziNqIB36/z3QXYoZa4lMi1SIlVj3UEp/6Yi1dhnAgEFB5eXl0vrS0\nVH6//7APWFFRe9j7xgu/36eysmrT3YgJaolPiVSLlFj1UEt8ivdaOnuB0OXb0ZMmTdLq1aslSRs2\nbFAgEOAtaAAAYqDLkXB2draysrKUm5sry7K0dOlSFRUVyefzaerUqZo7d6527dqlb775Rtdff72m\nT5+uadOm9UbfAQDo07p1TXjBggXt5seMGROdfuKJJ2LbIwAAjhJ8YxYAAIYQwgAAGEIIAwBgCCEM\nAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEII\nAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQ\nwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAh\nhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBg\nCCEMAIAhhDAAAIYQwgAAGEIIAwBgCCEMAIAhhDAAAIYQwgAAGEIIAwBgiKs7GxUUFKikpESWZSkv\nL08TJkyIrvvrX/+qxx9/XE6nU+eff75uu+22Huvsgazdu9Wv4H45gsFeO6YkKcmltFC4d4/ZU7pb\ni233fF+OVCI8L62/575US3f+bfSlerpispZYn4c8Lx1qGjJEwWUPS65uReQR6fII69at05YtW1RY\nWKjNmzcrLy9PhYWF0fUPPvignnnmGQ0ePFgzZ87UJZdcohNOOKFHO93K+c3XSn75d7IikV45XltJ\nvX7EnkMt8SmRapESqx5qiU+xqqUprb9qFi2RnZ4RoxY712UIFxcXKycnR5I0cuRIVVVVKRgMyuv1\natu2berfv7+OOeYYSdLkyZNVXFzcayEcPnui9mzcIoUaeuV4rQYN8qq8vJdH3z3kO9ViWT3bmSOU\nMM+LJQ0a5FN5ebXpnnRfF/82+lw9h2C8lhieh8ZriaFY1mKnpEpJvfPypMsQLi8vV1ZWVnQ+IyND\nZWVl8nq9KisrU0ZGRrt127Zt65medsL2pUm+Xj2k5PfJVnIvH7SHJFItg3yy7QR5XT/QJ7vJY7oX\nsZPhkx1xm+5FbCRSLek+2eGef8u1V/TRWr5zj+0jvCaRnp4ql8t5RG3EA7+/t5O/51BLfEqkWqTE\nqoda4lNfrKXLEA4EAiovL4/Ol5aWyu/3d7hu9+7dCgQCh2yvoqL2cPsaN/x+n8rKEuMtHGqJT4lU\ni5RY9VBLfIr3Wjp7gdDlnyhNmjRJq1evliRt2LBBgUBAXq9XkjR8+HAFg0Ft375d4XBY77zzjiZN\nmhTDbgMAkLi6HAlnZ2crKytLubm5sixLS5cuVVFRkXw+n6ZOnar8/HzdddddkqTvfe97Ov7443u8\n0wAAJIJuXRNesGBBu/kxY8ZEp88444x2f7IEAAC6h2/MAgDAEEIYAABDCGEAAAwhhAEAMIQQBgDA\nEEIYAABDLPtIv4cSAAAcFkbCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGBIt+6ilKgKCgpU\nUlIiy7KUl5enCRMmHLTNY489po8++kgvvPCC1q5dqzvuuEOjRo2SJJ144om69957tXPnTi1evFjh\ncFgul0uPPPKI/H6/srKylJ2dHW3rueeek9PpjOtaFi1apA0bNmjAgAGSpNmzZ2vKlCl6/fXXtWLF\nCjkcDk2fPl3XXHNNj9QRy1rmzp2riooKSVJlZaVOOeUU3XzzzZo2bZrGjx8vSUpPT9cTTzwRN7VI\n0uuvv66nn35aLpdLc+fO1ZQpU7Rz504tXLhQkUhEfr9fjzzyiDweT68+L7Gup6+dM53V0hfPmc5q\n6YvnzH/+53/q9ddfj6779NNP9eGHH+qLL75Qfn6+JGn06NG6//77JUlPP/203nrrLVmWpTlz5mjy\n5Mk9Vku32EeptWvX2jfddJNt27a9adMme/r06Qdt89VXX9kzZsywZ86cadu2ba9Zs8a+/fbbD9pu\n4cKF9htvvGHbtm2vXLnS/sUvfmHbtm2feeaZPdX9dmJZyz333GP/z//8T7tlNTU19sUXX2zv27fP\nrqurs7///e/bFRUVPVBJbGtpa9GiRXZJSYm9bds2+4orroh9xztwOLXs3bvXvvjii+3q6mp79+7d\n9pIlS6L9f/PNN23btu3HHntNCgqnAAAGNElEQVTMXrVqVa8+L7Gupy+eM53V0hfPmc5qaauvnDMH\n7p+fn2/btm3PnDnTLikpsW3btu+880773Xfftbdu3WpfccUVdigUsvfs2WNfcskldjgc7sGKunbU\nvh1dXFysnJwcSdLIkSNVVVWlYDDYbpuHHnpI8+fP77KtpUuX6pJLLpHU/CqxsrIy9h0+hFjW0pGS\nkhKddNJJ8vl8Sk5OVnZ2ttavX3/E/e5IT9Ty9ddfq7q6usNX1D3pcGopLi7WxIkT5fV6FQgE9MAD\nD0iS1q5dq4suukiSdMEFF6i4uLhXn5dY19MXz5nOaulIvJ8zXdXSl86Ztn7961/r1ltvVUNDg779\n9tto/1vPmbVr1+q8886Tx+NRRkaGhg0bpk2bNvVsUV04akO4vLxc6enp0fmMjAyVlZVF54uKinTm\nmWdq2LBh7fbbtGmTbrnlFl177bV67733JEmpqalyOp2KRCJ68cUXNW3aNElSQ0OD7rrrLuXm5urZ\nZ5/tE7VI0sqVKzVr1izNnz9fe/fuVXl5uTIyMjptP55rkaTnn39eM2fObHeMuXPnKjc3t93bWLF2\nOLVs375d9fX1uuWWW/TDH/5QxcXFkqS6ujp5PB5J0sCBA1VWVtarz0us6+mL50xntUh975w5VC1S\n3zpnWn388cc65phj5Pf7VVFRobS0tOg6U+dMdxzV14Tbstt8e2dlZaWKior07LPPavfu3dHlxx13\nnObMmaN//Md/1LZt2zRr1iz9/ve/l8fjUSQS0cKFC3X22Wdr4sSJkqSFCxfqBz/4gSzL0syZM3X6\n6afrpJNOiuta/umf/kkDBgzQ2LFj9dRTT2n58uU69dRTO20/nmvxeDxqaGjQBx98EL02NGDAAN1x\nxx36wQ9+oOrqal1zzTU6++yzFQgE4qKW1nXLly/Xjh07NGvWLL3zzjudttOd5T3lSOqxLKvPnTOd\n1dIXz5nWdR09L33xnJGkV155RVdccUWX7XRneW86akfCgUBA5eXl0fnS0lL5/X5J0po1a7R3715d\nd911mjNnjjZs2KCCggINHjxY3/ve92RZljIzMzVo0KDoP4bFixfr2GOP1Zw5c6JtXnvtterXr59S\nU1N19tlna+PGjXFfy8SJEzV27FhJ0oUXXqiNGzd22H5PnYCxfl7ef//9dm+peb1eXXXVVXK73crI\nyND48eP19ddfx00tAwcO1KmnniqXy6XMzEz169dPe/fuVWpqqurr6yVJu3fvViAQ6NXnJdb1SH3v\nnOmslr54zhzqeelr50yrtWvXRl/8ZGRktLvE0dk507rcKBMXouPBBx98YN9www22bdv2p59+aufm\n5na43bZt26IfAHjttdfsp59+2rZt2y4tLbWnTJlih0Ih+7XXXrPz8vLa7bd582b7zjvvtJuamuzG\nxkZ7xowZ0Q8JxHMtc+bMsbdu3WrbdvMHZvLz8+26ujo7JyfHrqqqsoPBYPQDJ/Fei23b9m9/+1v7\n+eefj+5XXFxsFxQU2La9/8Mzu3btiptadu3aZd9www12JBKx9+7da0+ZMsWORCL2kiVL7FdffdW2\nbdt+4IEH7JdffrlXn5dY19MXz5nOaumL50xntdh23ztnWus58MNjP/7xj+3333/ftm3bvuWWW+z3\n3nvP/vbbb+3LLrvMDoVC9q5du+yLL744WrcpR+3b0dnZ2crKylJubq4sy9LSpUtVVFQkn8+nqVOn\ndrjPhRdeqAULFujtt99WY2Oj8vPz5fF49OKLLyoUCun666+X1PyBgvz8fA0ZMkRXX321HA6HLrzw\nwh77kEMsa7nuuus0b948paSkKDU1VT//+c+VnJysu+66S7Nnz5ZlWbrtttvk8/nivhZJKisrU2Zm\nZnTb008/Xa+++qpmzJihSCSim266SYMHD46bWgYPHqxLLrlE06dPlyQtWbJEDodDt99+u+655x4V\nFhZq6NChuvzyy+V2u3vteYl1PX3xnOmslr54znRWi9T3zpnWPre91itJeXl5uu+++9TU1KSTTz5Z\n55xzjiRp+vTpmjlzpizLUn5+frRuU7iVIQAAhhy114QBADCNEAYAwBBCGAAAQwhhAAAMIYQBADCE\nEAYAwBBCGAAAQwhhAAAM+f9c5TdcLTsjZwAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "peoHmV2M40uU",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 721
+ },
+ "outputId": "f3b9cef6-5cb0-4fe4-dbcc-b31d0e3da01a"
+ },
+ "cell_type": "code",
+ "source": [
+ "linear_regression(learning_rate=0.0000006, n_epochs=1000,interval=50)"
+ ],
+ "execution_count": 29,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.03985174\n",
+ "Loss after epoch 50 is 0.03985032\n",
+ "Loss after epoch 100 is 0.039848898\n",
+ "Loss after epoch 150 is 0.03984747\n",
+ "Loss after epoch 200 is 0.039846055\n",
+ "Loss after epoch 250 is 0.039844636\n",
+ "Loss after epoch 300 is 0.039843213\n",
+ "Loss after epoch 350 is 0.03984179\n",
+ "Loss after epoch 400 is 0.03984037\n",
+ "Loss after epoch 450 is 0.039838947\n",
+ "Loss after epoch 500 is 0.039837524\n",
+ "Loss after epoch 550 is 0.039836105\n",
+ "Loss after epoch 600 is 0.039834686\n",
+ "Loss after epoch 650 is 0.039833266\n",
+ "Loss after epoch 700 is 0.039831843\n",
+ "Loss after epoch 750 is 0.039830424\n",
+ "Loss after epoch 800 is 0.039829005\n",
+ "Loss after epoch 850 is 0.03982759\n",
+ "Loss after epoch 900 is 0.03982617\n",
+ "Loss after epoch 950 is 0.039824747\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 0.5196233\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAeEAAAFKCAYAAAAqkecjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzt3Xt8VPWd//H3mVtuM0gSJ4Bc1B8g\n2CBKRAviBRW020qrqCQqsrpsERURNIuYoomVpNbbbhXb1dUiCmpcNz91H7rSauXXrg2goqBplQIW\nwjUJJCETcplMzu+PJEMCCeGS5DsZXs/HI48553vO+Z7vh3Ae75xzZuZYtm3bAgAAPc5hegAAAJys\nCGEAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAxx9fQOS0urenqXXS4xMV7l5QdMD6NLUEtkiqZapOiq\nh1oiU6TX4vf72m3nTPg4uFxO00PoMtQSmaKpFim66qGWyNRbayGEAQAwhBAGAMAQQhgAAEMIYQAA\nDCGEAQAwhBAGAMAQQhgAAEMIYQAADCGEAQAwhBAGAMCQHv/uaAAAIkl9qF47Azu0PVCs7VXFcjvc\nmjr8RlmW1e37JoQBAFHtQPCAtlcVa3tgm4qrmoK2uGpb+HV39S7Zsttsc+mgy+WP93f72AhhAECv\nVllXoR27N2vDtm+0vepg0G6v2qbtgWKV1ZS1u53Tcuo070CNO+0iDfIO1mDfYA32na5z/KN7JIAl\nQhgAEMFs21ZpTamKq7Y2n7k2h2vLdKBYVfX72902xhmjQb7BSk0+R4N9QzTIN1iDfIM12DdEg31D\n1D9hgFwOszFICAMAjGlobNDu6l3aXlWsbc1BG75cHCjWjqrtqg3Vtrut1+1rPnsdouEpQ5Xs6q/B\nzUE7yDdE/ji/HFZkv/+YEAYAdJvahlrtDGxXcfg+7LbwGez2qmLtDOxQyA61u21ybLJGJJ0dPoMd\n4huiQc1ntIO9g3VKTN/wm6f8fp9KS6t6srQuQQgDAA4TagwpEKxSVX3Tz/76/QrU72+aD7fvV6B5\neVNb0/JA622C7QejJUv9EwYord/YprNXb3O4Nt+XHegbpAR3Qg9X3fMIYQCIIsFQUFXB/eHwDDSH\nZVWrQK2qr1RVfZWCjlqV7t+nqmDVwYBt/jnQUH1c+3c5XOrj6SOvp49O73OGEmMTm85kvYPb3Jcd\n6B0kj9PTxdX3PoQwABwj27bV0NigBrtBDY3BpunGUNO03dA833BwnVBTe6gxpGDz+iG7aZtgY1Ch\ncF+tf1r6CoX3UReqC59tVgWrVFW3/7Az0I7un3Ym1hkrr8cnn8enfgn95XM3Tbe0+dx9ml5j+jQv\na55vWad5eYwzpkc+XxstCGEAES0YCqouVKuahlrVhWpV21CrmlCN6hpqVRuqVW1DjWob6lQbqlFd\n82vrdWtbXhtq2rTVh+rDYRhsDr5QY0NTSNqh8HRTQIYUDAWbg7Ohw3uYJsS7EuTz+NQ3pq8G+wbL\n6+kTDtCDIdm2rY/nFHk9Pp3Rf4DqA5a8bh9npYYQwoAhtm2rLlSnmoYDqmmoUW1DjQ401CjU2KDE\nYILKy9teDjz0ywRa99PhPjrapoP2I/XX8f6lhsbgwbBrDsOallBsqJEjplH79u/vMChbQrYpKJu2\nqW1+7c7Ac1pOuRwuOS2X3E63XJZTTodLbodbTodLMc4YuRwuuRzuplfLqbiYWNkhq3k9l1yWK7yN\ny+Fs6qt5e5fD2TRtueRqXt/ZvI3L6W56dThb9e9q3p/r4H6bx+RyuBTjjD0Yru6mM9AT+YiNP9Gn\n0obe92amaEIIA4foKBxb5msaalQTbJ4O1agm2HpZq3U62KY2VKMDzdscKQxPJjHOGMU4YxXrilWs\nM1bJcacq1hWnGGeMYl1xig2/Hlwnpvm19fIYZ4ziXHGKdcU299dq2/D6Tcs8Ts9xfXylt74LF5GJ\nEEZEsm1bwcag6kN1qgvVN7/WqT5Ur7rGOtW3TIfqwuvE7nZob8X+Nm217YVhD4ejJUtxrnjFu+MU\n54pXUmyyBnrjw2ER52qajnfFK9YVK5fDrfg4jw7U1LfbV7v7OMI9uC7dpoN2l9PVKiDjDgvKAacm\nq6Yq1BSUrhjFOVsHZWzEf5YT6C6EMNpVF6pToD6gQLBKgfqAqoPVqg3VtBuKbdoa27YFW4Ky8ZAg\nbbNt83Rj2767W0fh2BSMcW3CsWU+HJru1u1xim1+jXPFK77VtnHueHkcnmN+o0q0nW1FWz1AVyGE\no0QwFGwKzGAgHJ7VwepW0y3tB4M1EAyoXjXaV13RannTdsHGYLeO1+1wy+OMUYzTI48zRh5njBLc\nCYe1xTg9cjs8h7Udtp7Do+S+p6j+gC1Pq+UdhWPLpUvexQnApKMK4by8PK1fv16WZSkrK0ujR48+\nbJ2nnnpKX375pV599dUuH2Q0CjWGmoKvVfi1N13dJkzbBmggGFB1fdO6J3Lm6HK45HV75XX71D9h\ngBLc3qZ5j09et1cJ7gR53T7FumKbQ685QB0x8jg9imkOwoPTh7Q5Yg4JzeO7F9cZzrYA9DadhvDa\ntWu1detW5efna/PmzcrKylJ+fn6bdTZt2qRPP/1Ubre72wbanr01e/XUZ4+pqr5KjXajGu1G2Wps\nnrbDbY1qlN0y3fpHttSyntous1utc2ib5ZQaGkJt+mmvf7tNn3Zzm61QY8Nxf5ZPkhyWIxyUSbHJ\nGtLndHndPiV4msOzVYAeGqYJh7SfedoA7d9XzxkhABjQaQgXFhZq0qRJkqShQ4eqsrJSgUBAXq83\nvM5jjz2m+fPna8mSJd030nZ8s+8vevGr57usP4flaPqRIzxtWY5W7ZYsy5LT4ZRs62B784/T4ZJb\nh7dbcsiyrDb9JLi98nqag9HdHIyeprNRbzthmtCyzO1VnCuuy0Iz1hWrKqt7Lz0DANrXaQiXlZUp\nNTU1PJ+UlKTS0tJwCBcUFOjCCy/UwIEDu2+UHZgw8BJ9fdumps8hWocEZzhIrXbbLcs6JGyPPtS4\n7AkA6ArH/Mas1h/kr6ioUEFBgZYuXao9e/Yc1faJifFyuZzHutsO+eXrsr6Oab9+M/vtDtQSmaKp\nFim66qGWyNQba+k0hFNSUlRWVhaeLykpkd/vlyStXr1a+/bt0y233KL6+npt27ZNeXl5ysrK6rC/\n8vIDXTBss6LpTJhaIlM01SJFVz3UEpkivZaO/kDo9C2qEyZM0MqVKyVJRUVFSklJCV+K/sEPfqD3\n339fb775ppYsWaLU1NQjBjAAADio0zPhtLQ0paamKiMjQ5ZlKTs7WwUFBfL5fJo8eXJPjBEAgKh0\nVPeEMzMz28yPHDnysHUGDRrEZ4QBADgGfGErAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhC\nCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACG\nEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACA\nIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMA\nYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYAghDACAIYQwAACGEMIA\nABhCCAMAYAghDACAIYQwAACGEMIAABhCCAMAYIjraFbKy8vT+vXrZVmWsrKyNHr06PCyN998U2+9\n9ZYcDodGjhyp7OxsWZbVbQMGACBadHomvHbtWm3dulX5+fnKzc1Vbm5ueFlNTY3ee+89rVixQm+8\n8Ya2bNmiL774olsHDABAtOg0hAsLCzVp0iRJ0tChQ1VZWalAICBJiouL07Jly+R2u1VTU6NAICC/\n39+9IwYAIEp0ejm6rKxMqamp4fmkpCSVlpbK6/WG21544QW98sormjFjhgYPHnzE/hIT4+VyOU9g\nyJHB7/eZHkKXoZbIFE21SNFVD7VEpt5Yy1HdE27Ntu3D2mbNmqUZM2bopz/9qc4//3ydf/75HW5f\nXn7gWHcZcfx+n0pLq0wPo0tQS2SKplqk6KqHWiJTpNfS0R8InV6OTklJUVlZWXi+pKQkfMm5oqJC\nn376qSQpNjZWl156qdatW9cV4wUAIOp1GsITJkzQypUrJUlFRUVKSUkJX4puaGjQwoULVV1dLUn6\n6quvdOaZZ3bjcAEAiB6dXo5OS0tTamqqMjIyZFmWsrOzVVBQIJ/Pp8mTJ+vuu+/WjBkz5HK5NGLE\nCF155ZU9MW4AAHq9o7onnJmZ2WZ+5MiR4empU6dq6tSpXTsqAABOAnxjFgAAhhDCAAAYQggDAGAI\nIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAY\nQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAA\nhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwA\ngCGEMAAAhrhMDwAA0LOeffZf9e23f1VlZbmqqw/otNMGqk+fU5SX90SX9H/DDVOUktJPDsfB87wl\nS1444X7/93//n77//Yu0f3+lXnrpeS1Y8LMT7tM0QhgATjL33DNfkvSnP/1e69cXac6ceV2+jyef\nfEbx8fFd2ucbb6xQWtoFSk4+NSoCWCKEAQDN1q37TG+8sVwHDhzQnDnzdf/9c/Teex9JkhYtWqCp\nU6dp5MizlZf3iKqqqhQKhTRv3r9o2LDhR9X/j3505WH9ffHF56quDmjbtq3asWO75s69X+PHT9AH\nH7ynt97Kl2VZysi4RcFgUH/5y9fKzJyrhQsf0iOPLNJLL72qdes+0wsv/FpxcTHq2zdZDz74sD78\ncKU2bPhSFRXl2rZtq26++VZdc8213fbvdiIIYQAwKOfPi/Tfm9/u0j6nDL1WORctPq5tN2/epNdf\nL5DH42l3+Ztvvq7vf/8iTZlyrb77bot+9asn9W//9usTGa5KSvboySef0erVf9Y77/yXzj33PL38\n8otatux11dcHlZubrccee1ovvvjvevLJZ1RZWRHe9sknf6F//dfnNGrUcD344CL9/vcfyLIsbd68\nSf/+77/V9u3Fys7OIoQBAJFv2LDhHQawJH311QZVVJRr5cr3JUl1dbXtrpeZOTd8T7hv30QtXvzL\nDvscPfo8SVJKSooCgYD+/vfvNGTIGYqJiVVMTKwee+zpdrfbv79SlmWpX7/+kqS0tLH68st1Ouus\nkRo1arScTqf8/hRVVwc6L9wQQhgADMq5aPFxn7V2B7fb3W57Q0ND83KX5s//F40aNfqI/XR2T7il\nP0lyOp3hadu25XA4ZduNRzFaS7Zth+eCwaAsy9Fun5GKjygBANplWZZqa2tVW1urjRu/lSR973uj\n9Mc/rpIkfffdFr3xxvIT6q89p59+hrZt26oDBw6orq5O8+bdJdu2ZVkOhUKh8Hp9+vSRZVnavXu3\nJOnLL9dp5Mizj6NSczgTBgC069prb9CsWf+oM874PxoxoincbrghXbm5Obrrrn9WY2Oj5s3LPKH+\n2hMXF6eZM2dr3ry7JEnp6TfLsiyNGZOmu+6aqZ/9LCe87oIFi/TIIz9TXFyM/P7+uvLKq/S73/3P\n8RVsgGX38Hl6aWlVT+6uW/j9vqioQ6KWSBVNtUjRVQ+1RKZIr8Xv97XbzuVoAAAMIYQBADCEEAYA\nwBBCGAAAQwhhAAAMIYQBADCEzwkDwElm166dmjEjQ+ecM0r19Q2qr6/XLbf8oy677PJj7uu//itf\nFRUVuvTSifrjH1dp5sw72l2v5TGEHX0jV2tbtmzS008/ftjjDy+77Ps655xzw/PJycl65JFfHPOY\nD/Xxxx/q8ssn6W9/+/aINXQHQhgATkJDhpyuV199VaWlVdq/v1K3336Lxo0br5iY2OPqb/jwERo+\nfESHy1seQ3g0IdwRr9fbJc8lPtTy5ct0+eWTOq2hOxxVCOfl5Wn9+vWyLEtZWVkaPfrgd4auXr1a\nTz/9tBwOh84880zl5ua2eZAzACCy9elzipKTT9XevXu1dOl/yOVya//+Cv3854/p8cdztXPnDjU0\nNOif/3m2zj//An322Vo988xTSkpKVnLyqTrttIFat+4zFRS8qcWLHz/iYwh/9avf6N13/68+/PAD\nWZZDl1wyUTfdNF0lJXv00EML5Xa7NWzYWUc99l27dmrRogf07rtNT6KaOfNWLV78S/32ty/o1FP9\n+vbbv2rPnt16+OHFGjFipFasWKZVqz6SZTk0e/YcffPNX7Rp00ZlZf2LbrghPVzDRx/9Xvn5K+R0\nOjVixNmaNy9TL730fLuPXTwRnYbw2rVrtXXrVuXn52vz5s3KyspSfn5+ePnDDz+sV155Rf3799fc\nuXP1pz/9SZdddtkJDQoAThYJOYsU899d+yjDuinXqjrn6B8KsWvXTu3fX6mUlH6Smr6T+YEHfqYP\nPnhPycmn6sEHH1ZFRYXuvXe2li17Q88/v0QPPfSohg8/S5mZc3XaaQPDfR04UH3ExxCWlpZo1aqP\n9OtfvyRJuvPOmbr88kkqKMjXlVdepWnTbtLy5S9r06aNJ/zvUF9fr6efXqK3335LH3zwnuLj47Vq\n1Ud6/vmXtXPnDi1f/rIWLnxIK1YsU17eE1q37rPmGg7ohRee09Klryk+Pl4LFswPLzv0sYvdHsKF\nhYWaNGmSJGno0KGqrKxUIBCQ1+uVJBUUFISnk5KSVF5efkIDAgB0v23bturWW29VfX2DPB6PFi16\nRC5XUyR873upkqSvv96g9eu/0IYNX0qS6urqFAwGtWvXLg0f3nS2et55aaqrqwv329ljCP/61yJt\n316se+5puu964EC1du/eqb///TtdfnlT1owZM1arV//5sDEHAgHNmTMrPD906DBlZEzvsMZzzx0j\nSfL7++kvfynSxo3f6nvfGyWHw6FBgwZr4cKH2t2uuHibBg0aEn4K1Jgx52vjxm8kHf7YxRPVaQiX\nlZUpNTU1PJ+UlKTS0tJw8La8lpSU6JNPPtG99957woMCgJNFdc7iYzpr7Sqt7wkfyuVyh19nzPgn\nTZ78gzbLW99yPPTxA509htDlcmv8+AlasOBnbdpXrFgWfgxhR9u3d0949+5dbeaP9IhEp9OhxsbO\nH5dgWW3ramgIKiYmpt0+T9QxvzGrvZ3u3btXs2fPVnZ2thITE4+4fWJivFwu5xHX6Q06+jLu3oha\nIlM01SJFVz29vZa6ugS5XE2Bd2gtsbFunXJKnPx+n8aNG6s//OEPuvnmG7V3714tW7ZM9913nwYM\n6K+qqlKdeeaZKipar/POO099+8YrJsat888fpZ//vFjx8Q65XC7Nnj1bv/3tb+VyOZWYGKeLLhqr\n//iP5+T1uhQbG6vc3FxlZmZqxIjh2rFjiy655EJ9++1X8nhch43NsqzD2jyeRlVWljdnU6127dqh\npKSENnWcckqcYmPdGj9+rJYvX6rExDhVVFQoOztbzz33XPjfoaWGMWNStWvXdsXFWfJ6vSoqWq87\n77xThYWF8npj5ff7VF6e0O4Yj1WnIZySkqKysrLwfElJifx+f3g+EAjopz/9qebNm6eLL7640x2W\nlx84zqFGjkh/WsexoJbIFE21SNFVTzTUsm9ftRoams42D62ltjaoysoalZZWaezYi7Vq1Z90/fU3\nKhQK6Z/+aZZKS6t0++136O6756h//wFKSkpWdXWdKioOqK4uqOrqkG67bZamT58hqekxhGVlAY0e\nPUbTpqXr2Wdf0NSp6UpPv0kOh0OXXjpRVVVBXXPN9XrooYV6773/0dChw1Vf33DY2Gzbbuff3qG0\ntAt0/fXX64wzhmrYsLO0b191mzoqK2tUWxtUTMwpuvLKHyg9/SbZtq077rhbpaVVGjbsLF177XW6\n88654Rpmz75Ht912uyzLodGjz9Ppp4/Qhx+ukttdq9LSKpWXV7c7xo50FNadPspw3bp1evbZZ7V0\n6VIVFRVp8eLFev3118PLFy1apAsuuEA/+clPjmogvf0/rxQdB2ELaolM0VSLFF31UEtkivRaOgrh\nTs+E09LSlJqaqoyMDFmWpezsbBUUFMjn8+niiy/W22+/ra1bt+qtt96SJF1zzTVKT0/v2tEDABCF\njuqecGZmZpv5kSNHhqe//vrrrh0RAAAnCb5VAwAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAM\nIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAA\nQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYA\nwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQB\nADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADCEEAYAwBBCGAAAQwhh\nAAAMIYQBADCEEAYAwBBCGAAAQwhhAAAMIYQBADDkqEI4Ly9P6enpysjI0IYNG9osq6ur0wMPPKCp\nU6d2ywABAIhWnYbw2rVrtXXrVuXn5ys3N1e5ubltlj/++OM6++yzu22AAABEq05DuLCwUJMmTZIk\nDR06VJWVlQoEAuHl8+fPDy8HAABHr9MQLisrU2JiYng+KSlJpaWl4Xmv19s9IwMAIMq5jnUD27ZP\naIeJifFyuZwn1Eck8Pt9pofQZaglMkVTLVJ01UMtkak31tJpCKekpKisrCw8X1JSIr/ff9w7LC8/\ncNzbRgq/36fS0irTw+gS1BKZoqkWKbrqoZbIFOm1dPQHQqeXoydMmKCVK1dKkoqKipSSksIlaAAA\nukCnZ8JpaWlKTU1VRkaGLMtSdna2CgoK5PP5NHnyZM2dO1e7d+/Wd999p1tvvVXTpk3TlClTemLs\nAAD0akd1TzgzM7PN/MiRI8PTzzzzTNeOCACAkwTfmAUAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGE\nMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAI\nIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAY\nQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAA\nhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwA\ngCGEMAAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYclQhnJeXp/T0dGVkZGjDhg1tlv35z3/W\nDTfcoPT0dD333HPdMkgAAKJRpyG8du1abd26Vfn5+crNzVVubm6b5YsXL9azzz6r119/XZ988ok2\nbdrUbYMFACCauDpbobCwUJMmTZIkDR06VJWVlQoEAvJ6vSouLtYpp5yiAQMGSJIuu+wyFRYWatiw\nYd076mYJOYsU899v98i+2nBYSmq0e36/3YFaIlM01SJFVz3UEpm6sJa6KdeqOmdxl/TVmU5DuKys\nTKmpqeH5pKQklZaWyuv1qrS0VElJSW2WFRcXH7G/xMR4uVzOExhyK/EeyWF1TV/HyGlov92BWiJT\nNNUiRVc91BKZuqqW+HiP4v2+LumrM52G8KFs+8T+0igvP3BC27ex4OGmnx7m9/tUWlrV4/vtDtQS\nmaKpFim66qGWyNTltXTxv4u/g1Dv9J5wSkqKysrKwvMlJSXy+/3tLtuzZ49SUlJOdKwAAJwUOg3h\nCRMmaOXKlZKkoqIipaSkyOv1SpIGDRqkQCCg7du3q6GhQR9//LEmTJjQvSMGACBKdHo5Oi0tTamp\nqcrIyJBlWcrOzlZBQYF8Pp8mT56snJwc3X///ZKkH/7whzrzzDO7fdAAAESDo7onnJmZ2WZ+5MiR\n4ekLLrhA+fn5XTsqAABOAnxjFgAAhhDCAAAYQggDAGAIIQwAgCGEMAAAhhDCAAAYQggDAGAIIQwA\ngCGWfaJPZAAAAMeFM2EAAAwhhAEAMIQQBgDAEEIYAABDCGEAAAwhhAEAMOSoniccrfLy8rR+/XpZ\nlqWsrCyNHj36sHWeeuopffnll3r11Ve1Zs0a3XvvvRo+fLgk6ayzztJDDz2kXbt26cEHH1RDQ4Nc\nLpeeeOIJ+f1+paamKi0tLdzXyy+/LKfTGdG1LFy4UEVFRerbt68kaebMmZo4caLeffddLVu2TA6H\nQ9OmTdONN97YLXV0ZS1z585VeXm5JKmiokLnnXee7rjjDk2ZMkWjRo2SJCUmJuqZZ56JmFok6d13\n39WLL74ol8uluXPnauLEidq1a5cWLFigUCgkv9+vJ554Qh6Pp0d/L11dT287ZjqqpTceMx3V0huP\nmf/8z//Uu+++G1729ddf64svvtA333yjnJwcSdKIESP0yCOPSJJefPFFffDBB7IsS3PmzNFll13W\nbbUcFfsktWbNGnvWrFm2bdv2pk2b7GnTph22zt/+9jc7PT3dnj59um3btr169Wr7nnvuOWy9BQsW\n2O+9955t27a9fPly+5e//KVt27Z94YUXdtfw2+jKWh544AH7D3/4Q5u26upq+6qrrrL3799v19TU\n2D/60Y/s8vLybqika2tpbeHChfb69evt4uJi+7rrruv6gbfjeGrZt2+ffdVVV9lVVVX2nj177EWL\nFoXH//7779u2bdtPPfWUvWLFih79vXR1Pb3xmOmolt54zHRUS2u95Zg5dPucnBzbtm17+vTp9vr1\n623btu377rvPXrVqlb1t2zb7uuuus+vq6uy9e/faV199td3Q0NCNFXXupL0cXVhYqEmTJkmShg4d\nqsrKSgUCgTbrPPbYY5o/f36ucMT3AAAFvElEQVSnfWVnZ+vqq6+W1PRXYkVFRdcP+Ai6spb2rF+/\nXuecc458Pp9iY2OVlpamdevWnfC429MdtWzZskVVVVXt/kXdnY6nlsLCQo0fP15er1cpKSl69NFH\nJUlr1qzRlVdeKUm6/PLLVVhY2KO/l66upzceMx3V0p5IP2Y6q6U3HTOtPffcc7rrrrtUX1+vHTt2\nhMffcsysWbNGl1xyiTwej5KSkjRw4EBt2rSpe4vqxEkbwmVlZUpMTAzPJyUlqbS0NDxfUFCgCy+8\nUAMHDmyz3aZNmzR79mzddNNN+uSTTyRJ8fHxcjqdCoVCeu211zRlyhRJUn19ve6//35lZGRo6dKl\nvaIWSVq+fLlmzJih+fPna9++fSorK1NSUlKH/UdyLZL0yiuvaPr06W32MXfuXGVkZLS5jNXVjqeW\n7du3q7a2VrNnz9bNN9+swsJCSVJNTY08Ho8kKTk5WaWlpT36e+nqenrjMdNRLVLvO2aOVIvUu46Z\nFhs2bNCAAQPk9/tVXl6uPn36hJeZOmaOxkl9T7g1u9W3d1ZUVKigoEBLly7Vnj17wu1nnHGG5syZ\no3/4h39QcXGxZsyYod/97nfyeDwKhUJasGCBxo0bp/Hjx0uSFixYoB//+MeyLEvTp0/X2LFjdc45\n50R0LT/5yU/Ut29fnX322XrhhRe0ZMkSjRkzpsP+I7kWj8ej+vp6ff755+F7Q3379tW9996rH//4\nx6qqqtKNN96ocePGKSUlJSJqaVm2ZMkS7dy5UzNmzNDHH3/cYT9H095dTqQey7J63THTUS298Zhp\nWdbe76U3HjOS9NZbb+m6667rtJ+jae9JJ+2ZcEpKisrKysLzJSUl8vv9kqTVq1dr3759uuWWWzRn\nzhwVFRUpLy9P/fr10w9/+ENZlqUhQ4bo1FNPDf9nePDBB3X66adrzpw54T5vuukmJSQkKD4+XuPG\njdPGjRsjvpbx48fr7LPPliRdccUV2rhxY7v9d9cB2NW/l08//bTNJTWv16vrr79ebrdbSUlJGjVq\nlLZs2RIxtSQnJ2vMmDFyuVwaMmSIEhIStG/fPsXHx6u2tlaStGfPHqWkpPTo76Wr65F63zHTUS29\n8Zg50u+ltx0zLdasWRP+4ycpKanNLY6OjpmWdqNM3IiOBJ9//rl922232bZt219//bWdkZHR7nrF\nxcXhNwC888479osvvmjbtm2XlJTYEydOtOvq6ux33nnHzsrKarPd5s2b7fvuu89ubGy0g8GgnZ6e\nHn6TQCTXMmfOHHvbtm22bTe9YSYnJ8euqamxJ02aZFdWVtqBQCD8hpNIr8W2bfs3v/mN/corr4S3\nKywstPPy8mzbPvjmmd27d0dMLbt377Zvu+02OxQK2fv27bMnTpxoh0Ihe9GiRfbbb79t27ZtP/ro\no/abb77Zo7+Xrq6nNx4zHdXSG4+Zjmqx7d53zLTUc+ibx26//Xb7008/tW3btmfPnm1/8skn9o4d\nO+xrrrnGrqurs3fv3m1fddVV4bpNOWkvR6elpSk1NVUZGRmyLEvZ2dkqKCiQz+fT5MmT293miiuu\nUGZmpj766CMFg0Hl5OTI4/HotddeU11dnW699VZJTW8oyMnJUf/+/XXDDTfI4XDoiiuu6LY3OXRl\nLbfccovmzZunuLg4xcfH6xe/+IViY2N1//33a+bMmbIsS3fffbd8Pl/E1yJJpaWlGjJkSHjdsWPH\n6u2331Z6erpCoZBmzZqlfv36RUwt/fr109VXX61p06ZJkhYtWiSHw6F77rlHDzzwgPLz83Xaaafp\n2muvldvt7rHfS1fX0xuPmY5q6Y3HTEe1SL3vmGkZc+t7vZKUlZWlhx9+WI2NjTr33HN10UUXSZKm\nTZum6dOny7Is5eTkhOs2hUcZAgBgyEl7TxgAANMIYQAADCGEAQAwhBAGAMAQQhgAAEMIYQAADCGE\nAQAwhBAGAMCQ/w+MZE6Wb/+qmgAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "KjY_KnlE5ClG",
+ "colab_type": "text"
+ },
+ "cell_type": "markdown",
+ "source": [
+ "## Drive the loss to a minimum."
+ ]
+ },
+ {
+ "metadata": {
+ "id": "JKiHjGN15HPX",
+ "colab_type": "code",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 568
+ },
+ "outputId": "aa645a3d-25c6-4a9d-d7c0-972f6d14d003"
+ },
+ "cell_type": "code",
+ "source": [
+ "# YOUR CODE HERE\n",
+ "linear_regression(learning_rate=0.005, n_epochs=100001, interval=10000)"
+ ],
+ "execution_count": 30,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "text": [
+ "Loss after epoch 0 is 0.03985174\n",
+ "Loss after epoch 10000 is 0.00021830869\n",
+ "Loss after epoch 20000 is 5.600162e-06\n",
+ "Loss after epoch 30000 is 4.03015e-06\n",
+ "Loss after epoch 40000 is 4.019467e-06\n",
+ "Loss after epoch 50000 is 4.019467e-06\n",
+ "Loss after epoch 60000 is 4.019467e-06\n",
+ "Loss after epoch 70000 is 4.019467e-06\n",
+ "Loss after epoch 80000 is 4.019467e-06\n",
+ "Loss after epoch 90000 is 4.019467e-06\n",
+ "Loss after epoch 100000 is 4.019467e-06\n",
+ "Now testing the model in the test set\n",
+ "The final loss is: 4.6458417e-06\n"
+ ],
+ "name": "stdout"
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAe0AAAFKCAYAAAAwrQetAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4yLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvOIA7rQAAIABJREFUeJzs3XlclOX6x/HPLGwzgAiC5p64pLjn\nkksqbscW0+Mvy/TosSzLzBJXRBAQQXDNLfe0NAuPcdo0Lcs0y33ft3JXBFmEGWCYmef3hx3OsVRA\nBmaA6/16nZcO8zz3fV3C6cszz3KrFEVREEIIIYTDU9u7ACGEEEIUjIS2EEIIUUpIaAshhBClhIS2\nEEIIUUpIaAshhBClhIS2EEIIUUpo7V3AwyQlZdi7hCKrWFFHaqrR3mXYRFnqBcpWP9KLY5JeHJOj\n9+Lr6/HA9+RIu5hptRp7l2AzZakXKFv9SC+OSXpxTKW5FwltIYQQopSQ0BZCCCFKCQltIYQQopSQ\n0BZCCCFKCQltIYQQopSQ0BZCCCFKCQltIYQQopRw6IerOKIFC+Zy5swpUlJuk52dTdWq1fD0rEBM\nzEybjP/ii73x86uMWv3f36cWLlxW5HF37txO27btuXMnnZUrlzJhwuQijymEEKJkSWgX0qhRQQBs\n2vQ1v/12gXfeGW3zOWbNmo9Op7PpmJ999gktW7bGx6eSBLYQQpRSEto2cvDgfj77bC1Go5F33gli\n7Nh32LjxBwBCQyfQr99LPPFEQ2JiIsnIyMBisTB69Hjq1q1XoPGfe67bX8Y7dOgABkMmly9f4tq1\nq7z77ljatevA5s0b2bAhHpVKxYABg8jNzeXkyeOMG/cuwcFhREaGsnLlGg4e3M+yZR+g1Wrx9fVj\n0qQpbN26haNHD5OWlsrly5cYOHAwzz/ft9j+3YQQQhRcqQ7tiF9D+frCFzYds7d/XyLaT3ukfS9c\nOM+nnybg7Ox83/fXr/+Utm3b07t3X37//TfmzZvF++9/UJRyuXUrkVmz5rN79698+eXnNGvWnNWr\nV/DRR59iMuUSHR1ObOwcVqxYwqxZ80lPT8vbd9as6cydu4jKlaswZ04c33+/GZVKxYUL51my5EOu\nXr1CeHiIhLYQQtxHriWXhHP/4nn/Puid9CUyZ6kObUdTt269BwY2wLFjR0lLS2XLlk0A5ORk33e7\ncePezTun7eVVkWnT4h44ZtOmzQHw8/MjMzOTixd/p2bN2ri4uOLi4kps7Jz77nfnTjoqlYrKlasA\n0LJlKw4fPkj9+k/QuHFTNBoNvr5+GAyZ+TcuhBDl0AeH5xO9JxInjRP96vUvkTlLdWhHtJ/2yEfF\nxcHJyem+XzebzX+8ryUoaDyNGzd96Dj5ndP+z3gAGs1/H3yvKApqtQZFsRagWhWKouS9ys3NRaVS\n33dMIYQQ90rPSWPh4XlUdKlI95o9S2xeueWrmKhUKrKzs8nKyuLs2TMANGrUmB07fgLg999/47PP\n1hZ6vOzs7Lzx7qdWrdpcvnwJo9FITk4Oo0e/jaIoqFRqLBZL3naenp6oVCpu3rwJwOHDB3niiYaP\n0KkQQpQ/S44sIj0njZEtRuPpUqHE5i3VR9qOrG/fFxk+/J80aFCfBg3uhuGLL75MdHQEb7/9Olar\nldGjxxV6vNq16+SNdz9ubm4MG/YWo0e/DcDLLw9EpVLRokVL3n57GJMnR+RtO2FCKJGRk9FoNFSr\nVp1u3Xry3XffPlrDQghRTtzOus3SIx9Qyc2XYU2Gl+jcKsWBP/9MSsqwdwlF5uvrUSb6gLLVC5St\nfqQXxyS9OKai9jJ11xQWHnqfaR1iGd7sbRtWdpevr8cD35OPx4UQQogCSjQmsvLYUh7TV2VIwGsl\nPr+EthBCCFFA8w/MJsucxZhWE3DVupb4/BLaQgghRAFcy7jKRyc+pKZnbV554h92qUFCWwghhCiA\nOQdmYrKaGNdqIs6aBz+TozhJaAshhBD5+D39Nz49vYa6XvV4sf7LdqtDQlsIIYTIx+z9cZitZsa3\nnoRWbb+7peU+7UK6ceM6Q4YMoEGDJwAwmUwMGvRPOncOLPRYn38eT1paGp06dWHHjp8YNuzN+273\nn2U1H/TEtf/122/nmTNnxl+W8+zcuS1NmjTLe+3j40Nk5PRC1/xn27ZtJTCwO+fOnXloD0IIUVqd\nTTnDhrPxNPRuRJ+6/exai4T2I6hZs1ZeKN65k86rrw7iqafa4eLyaFcS1qvXgHr1Gjzw/f8sq1mQ\n0H4Qd3d3m6zL/Wdr135EYGD3fHsQQojSaua+6VgVKxPbhKJW2fcDagntIvL0rICPTyVu377NqlXL\n0WqduHMnjalTY5kxI5qkpJtkZeXw+utv8eSTrdm/fy/z58/G29sHH59KVK1ajYMH95OQsJ5p02Y8\ndFnNefMW89VX/2br1s2oVGqefroLr7zyD27dSiQsLBgnJyfq1q1f4Npv3LhOaOhEVq5cA8CwYYOZ\nNi2ODz9cRqVKvpw5c4rExJtMmTKNBg2eYPny5WzcuAmVSs1bb73D6dMnOX/+LCEh43nxxZfzevjh\nh++Jj/8EjUZDgwYNGT16HCtXLr3vMqJCCOHITiQf58sLCTTzbcEzjz9n73JKd2jrI0Jx+dq2S3Pm\n9O6LIaLgi5DcuHGdO3fS8fOrDNx9pvfEiZPZvHkjPj6VmDNnJufOXeG9997io48+Y+nShYSFRVGv\nXn3GjXuXqlWr5Y1lNBoeuqxmUtItfvrpBz74YCUAI0YMIzCwOwkJ8XTr1pOXXnqFtWtXc/782SL/\nO5hMJubMWcgXX2xg8+aN6HQ6tmzZwtKlq7l+/Rpr164mODiMTz75iJiYmRw8uP+PHowsW7aIVavW\nodPpmDAhKO+9Py8jKqEthHB0cfuiAZjUNhSVSmXnakp5aNvL5cuXeOedu8+bdXZ2JjQ0Eq327j9l\no0YBABw/fpQjRw4xePBxTCYzOTk55ObmcuPGDerVu3s03Lx5S3JycvLGzW9ZzVOnTnD16hVGjbp7\n3thoNHDz5nUuXvydwMDuALRo0Yrdu3/9S82ZmZl5NQP4+9dlwIAH32fYrFkLAHx9K3Py5AnOnj1D\ns2bNUKvVVK9eg+DgsPvud+XKZapXr5m3SlmLFk9y9uxp4K/LiAohhCM7lHiAzb9vpE2Vpwis0d3e\n5QClPLQNEdMKdVRsK/97TvvPtFqnvD+HDHmNgQP73/OM2/+skw1/XfYyv2U1tVon2rXrwIQJk+/5\n+ieffJS3rOaD9r/fOe2bN2/c8/phS35qNGqs1vyX/FSp7u3LbM7FxcXlvmMKIYQji917N18mtQ1z\niKNskFu+ik2jRo3ZuXM7AKmpKSxdugiASpV8uXz5IoqicOjQgXv2yW9ZzQYNGnLw4AGys7NRFIX3\n359FTk42NWvW4vTpkwB5H0UXhE6nJzU1BUVRuH07mevXrz5w27tzH8RsNpOScptJk+6uUGa13hu+\nNWrU4urVyxiNBgAOHTpIgwaNClyTEEI4gt3Xf2XblR94unoXOlR72t7l5CnVR9qOrGvX7hw8uI8B\nAwaQnW3itdfufjQ9fPjbhIZOpEqVx/LOg/9HfstqLliwjJdeeoWRI99ArVbTqVMXXFxc6d//FcLC\ngtmxYxv+/vUKXKOnpyetWrXh9deHULduvYde/f3YY1Xp06cP77wzHEVRePPNkQDUr9+AN94YwogR\n7+b1MHLke4wdOwqVSk3Tps1p1qw5+/fvKdS/nxBC2IuiKEzfGwVAcJvJ+Wxdsgq0NGdMTAxHjhxB\npVIREhJC06ZN/7LN7NmzOXz4MGvW3L0SecaMGRw4cACz2cybb75Jz549CQ4O5sSJE3h5eQEwbNgw\nunTp8sB5y8IycLKcneMqS/1IL45JenFM+fWy/co2+n/dhx61/sYnz/2rBCu762FLc+Z7pL13714u\nXbpEfHw8Fy5cICQkhPj4+Hu2OX/+PPv27cu7j3j37t2cO3eO+Ph4UlNT+fvf/07Pnj0BGDNmDIGB\nhX8QiRBCCFHcFEUh9o+j7IkOdpQNBTinvWvXLrp3v3vVnL+/P+np6X+58jc2NpagoKC8161bt2be\nvHnA3Y9gs7KysFgstqxbCCGEsLnvL23mQOJ+nq/Th6a+ze1dzl/ke6SdnJxMQEBA3mtvb2+SkpJw\nd3cHICEhgTZt2lCt2n/vN9ZoNHm3/GzYsIFOnTrlXTm8du1aVq1ahY+PD2FhYXh7ez9w7ooVdWi1\nmge+X1o87KOO0qYs9QJlqx/pxTFJL47pfr1YFSuzEqajQkXs36Idst9CX4j2v6fA09LSSEhIYNWq\nVSQmJv5l261bt7JhwwY+/PBDAPr06YOXlxcNGzZk2bJlLFy4kClTpjxwrtRUY2HLczjl6TxQaVOW\n+pFeHJP04pge1MvXF77g8M3D9KvXHz9VTbv1+7BfFvL9eNzPz4/k5OS817du3cLX1xe4e+46JSWF\nQYMG8c4773DixAliYmIA+Pnnn1myZAnLly/Hw+NuAe3ataNhw4YAdO3albNni/7kLiGEEKKoLFYL\ncXuj0ag0jG8dbO9yHijf0O7QoQNbtmwB4MSJE/j5+eV9NN6rVy82bdrE+vXrWbhwIQEBAYSEhJCR\nkcGMGTNYunRp3pXiAKNGjeLKlSsA7Nmzh3r1Cn57khBCCFFc/n1+A2dTz/Byg4H4ezluNuX78XjL\nli0JCAhgwIABqFQqwsPDSUhIwMPDgx49etx3n02bNpGamsro0aPzvhYXF8egQYMYPXo0bm5u6HQ6\npk8v+tKQQgghRFHkWnKZuW86TmonxrSaYO9yHqpA92nbS1k4f1IezgOVVmWpH+nFMUkvjunPvXxy\n8mOCfnqHVxu/TlynOQ/Zs2QU6Zy2EEIIUVblWHKYvT8OV40rQU+Ot3c5+ZLQFkIIUW6tPfkRVzOv\nMLTx61TRP2bvcvIloS2EEKJcMuYamXtgJjqtnlEtgvLfwQFIaAshhCiXVp9YyS1jIsObjsBX52vv\ncgpEQlsIIUS5k2nKYMHBOXg6V+Dt5qPsXU6BSWgLIYQod5YfXcLt7NuMaP4OXq4V7V1OgUloCyGE\nKFdSs1JZdHg+3q7eDG86wt7lFIqEthBCiHJlzq453DGlM7LFaDycPe1dTqFIaAshhCg3krOSeX/P\n+/i6+fFa4zfsXU6hSWgLIYQoNxYeep9MUyajnxyL3klv73IKTUJbCCFEuZBouMmq48up7lmdwY1e\ntXc5j0RCWwghRLkw7+BsssxZhHUKw1Xrau9yHomEthBCiDLvasYVPj6xilqetXm1eek8ygYJbSGE\nEOXA3AMzMVlNjGsVjJPGyd7lPDIJbSGEEGXab+kXWHdqDfW86vNi/ZftXU6RSGgLIYQo02bvi8Oi\nWJjQJgSNWmPvcopEQlsIIUSZdSblNBvOxtPIpzG9/fvau5wik9AWQghRZs3cNx0FheA2oahVpT/y\nSn8HQgghxH0cSz7KVxf+TQu/lvyt9jP2LscmJLSFEEKUSTP2RgMwsU0oKpXKztXYhoS2EEKIMudA\n4j62XPyWto+1I7BGN3uXYzMS2kIIIcqc2D3TAJjUJqzMHGWDhLYQQogyZtf1X9h+dRudqgfSvlpH\ne5djUxLaQgghygxFUZi+JwqA4DaT7VyN7UloCyGEKDO2X93G7hu/0rNWL1pVaVN8E2Vn47ZoPhUD\nO6A9cqj45vkTbYnNJIQQQhQjRVGI/eMoe2JxHWVbLLj86zP0cdForl3F6lkBpQSfsiZH2kIIIcqE\n7y5t5uCtA/T270sT32a2HVxRcP5+MxW7dsDz3RGok5MwjnyPlH1HsDRpatu5HkKOtIUQQpR6VsVK\n7J5pqFAxoXWITcfWHtiHPioc5193oqhUZA8YhGFCCNbqNWw6T4FqKfEZhRBCCBv75sKXnLh9jBfr\nv0wD7ydsMqbm/Dn0MVNx+eZLAHJ69sIQEo6lUYBNxn8UEtpCCCFKNYvVQtzeaDQqDeNaBxd5PHXi\nTXSz4nBduxqVxULuk60whE0lt739bx+T0BZCCFGqfX5uPefSzvKPhv+kTgX/Rx5HlXEHt0Xz0C1Z\nhMpoxOxfF0NIOKbnXwAHeUCLhLYQQohSK9eSy8x903FWOzOm1YRHG8Rkwu2jlejmzEB9+zYWv8oY\nI2PIHjgYnJxsW3ARSWgLIYQotT478wmX7lzktcZvUN2jkBeGWa24fPE5+pgoNJcvYnX3wBAcivHN\nkaDXF0/BRSShLYQQolTKNmcze18crhpXRj85rlD7Ov30I/qocJyOHUFxcsI4fATG0eNRKlUqpmpt\nQ0JbCCFEqbT25GquG64xotkoqugfK9A+2qOHIS4Kr++/ByC7X38MwaFYaz9enKXajIS2EEKIUseY\na+T9g7PRafWMahmU7/bqi7+jj43CNWEDAKYuXTGERWJuYuOHsBQzCW0hhBClzqrjK7hlTCToyXFU\ncnvwR9qq5GR0c2fgtnolqtxccps2x2n2TNKbtS3Bam1HQlsIIUSpkmnKYMGhOXg6V2BEs1EP2CgT\n3dJFuC2ajzozA0ut2hhCppDTpx++lStAUkbJFm0jEtpCCCFKlWVHF5OSnUJwm1C8XCve+2ZuLq6f\nfIx+5nTUSbew+viQETKD7CGvgbOzfQq2IQltIYQQpUZadiofHF6At6s3w5uO+O8bioLzN1+ij45E\n+9sFFJ0ew9iJZL09CsXD034F25iEthBCiFJj8ZEF3DGlE95uGu7OHgA4/boT/dQwnA4eQNFoyBo6\nDMPYYJTKle1cre0VKLRjYmI4cuQIKpWKkJAQmjb96zJks2fP5vDhw6xZswaAGTNmcODAAcxmM2++\n+SY9e/bkxo0bTJgwAYvFgq+vLzNnzsS5DHxcIYQQovglZyWz9Mhi/HSVebXx62hOnkA/LRyXrd8B\nkNO7L4aQMCz+9excafHJdz3tvXv3cunSJeLj44mOjiY6Ovov25w/f559+/blvd69ezfnzp0jPj6e\nFStWEBMTA8D8+fMZOHAg69ato1atWmzYsMGGrQghhCjLFhyci9FsILz6MCqPGUPFwPa4bP0OU/uO\npH77A3dWflymAxsKENq7du2ie/fuAPj7+5Oenk5mZuY928TGxhIU9N/75Fq3bs28efMA8PT0JCsr\nC4vFwp49e+jWrRsAgYGB7Nq1y2aNCCGEKLtuGm7wxd5lLN7mzohXZ+Mavw7LE41IX/cv0v+9EfOT\nre1dYonI9+Px5ORkAgL+u3aot7c3SUlJuLu7A5CQkECbNm2oVq1a3jYajQadTgfAhg0b6NSpExqN\nhqysrLyPw318fEhKSrJpM0IIIcqgrCzOhP6Dkxty8MrJwVK9BoaJk8l58WXQaOxdXYkq9IVoiqLk\n/T0tLY2EhARWrVpFYmLiX7bdunUrGzZs4MMPP3zoOA9SsaIOrbb0f0N8fT3sXYLNlKVeoGz1I704\nJumlCMxm+PhjzGGTefH6TdJ0aiwzpqMZ9S6erq5FGrq0fl/yDW0/Pz+Sk5PzXt+6dQtfX1/g7rnr\nlJQUBg0ahMlk4vLly8TExBASEsLPP//MkiVLWLFiBR4ed/9xdDod2dnZuLq6kpiYiJ+f30PnTk01\nFqU3h+Dr60FSKb2J/8/KUi9QtvqRXhyT9PKIFAXnLd+ij45Ae+Y0VicN0ztCpZDZ9G01DDJy7/7v\nETn69+Vhv1Dke067Q4cObNmyBYATJ07g5+eX99F4r1692LRpE+vXr2fhwoUEBAQQEhJCRkYGM2bM\nYOnSpXh5eeWN1b59+7yxvvvuO55++ukiNSaEEKJs0e7dg9cLvagwZACac2e51b8v9UYprHqxPr1b\nDrV3eXaX75F2y5YtCQgIYMCAAahUKsLDw0lISMDDw4MePXrcd59NmzaRmprK6NGj874WFxfHqFGj\nmDhxIvHx8VStWpW+ffvarhMhhBCllubsGfTRkbh8+w0AOb2ewzA5nJFXZnP5rJUVbSajUZf+06VF\npVIKcnLZThz544uCcvSPYQqjLPUCZasf6cUxSS/5U9+4jm7mdFzXrUFltZLbui2ZYVMxP9WOMymn\n6fRZWxr5NOaHl35Grcr3w+ECcfTvy8M+HpcnogkhhChxqjvp6Ba8j9uyD1BlZWGuVx/D5AhMzzwH\nKhUAM/bFoKAQ3DbUZoFd2kloCyGEKDk5ObitWo5u7kzUqalYqjyGMXoG2QMGgfa/kXQs6QhfX/iC\nln5P0rNWLzsW7FgktIUQQhQ/qxWXz9ejj52G5splrB6eZE4OJ+uNEfDHcz3+V9zeu0/fDG4bhuqP\nI28hoS2EEKI4KQpO27biHhWB9sQxFGdnjG+9g3H0WBRvn/vusv/mXr67tJl2VTvQuXpgCRfs2CS0\nhRBCFAvtoQPoo8Jx3rkDRaUiu/8ADMGhWGvUfOh+sf85ym4TKkfZfyKhLYQQwqbUv11APz0K1y8T\nAMjp1gPD5AgsjZvku+8v135mx9VtdKnRlXZVOxR3qaWOhLYQQgibUN26hX52LK5rVqMym8lt0RJD\n2FRyO3Yq0P6KohC7dxpw9yhb/JWEthBCiCJRZWbg9sECdB8sQGU0YH68DobJ4Zh69827fasgtl35\ngT03dvG32s/QsnKrYqy49JLQFkII8WhMJlzXrEY/Ow51chLWSr5kTplK9uCh4ORUqKEURSF2TxQA\nE9pMLoZiywYJbSGEEIVjteLy1b/Rx0xFc/F3rHp3DOMnYRwxCv5Ym6Kwlh9dzOGkQ7zg/3eaVGpq\n44LLDgltIYQQBeb083b0UVNwOnwIRasla9hwDEETUPJZtfFBrIqV6N2RLDg0l0pulQh5aoqNKy5b\nJLSFEELk78gRKgSNxXnbDwBk9+2HITgMax3/Rx4yx5LDez+OIOHcBupU8OfT5z/n8Qp1bFVxmSSh\nLYQQ4oHUly+hj50Gn6/HWVEwPd0ZQ1gk5uYtizRuWnYqQzcP4tfrO2ldpS0fP/MZPm73f9iK+C8J\nbSGEEH+hun0b3fszcVu1ApXJBM2bkzYpnNwuXQt1Rfj9XMm4zCvf/B9nU8/wfJ0+LOq+DDetm40q\nL9sktIUQQvyXwYBu+WLcFryPOuMOlpq1MASH4vnma+TeNhR5+KNJhxm4sT+3jIm82Wwkke2jZQWv\nQpDQFkIIAWYzrp+uRTcjBk3iTaze3mRGTSdr6Ovg4gLqogfrD5e+Y9iWf5JlNjKtQyzDm71tg8LL\nFwltIYQozxQF503foI+OQHv+HIqbG4agcWSNfA/Fs4LNpllzcjUTtgfhpHZi5d/W8Lz/CzYbuzyR\n0BZCiHJKu3sX7lPDcNq/F0WjIWvwqxjHB2Ot8pjN5rj7aNIo5h6YhberN2uejad1lbY2G7+8kdAW\nQohyRnP6FProCFy2fAtAzrO9MUwOx1Kvvk3nMVlMjN42kg1n46nt+TifPf85dbzq2nSO8kZCWwgh\nygn19WvoZsTg+tknqKxWctu2I3PKVMytbX/km56Txqub/8HOazt4snIr1jy7nkpulWw+T3kjoS2E\nEGWcKi0V3fy5uK1Ygio7G/MTDTGERmDq0avIt2/dz7WMq7yy8f84nXKKZx5/nsXdV6Bz0tl8nvJI\nQlsIIcqq7GzcVi5DN28W6rQ0LFWrYZg4mZyXXgGNplimPJZ8lEEb+3PTcIPXm7xJVIdYNOrimas8\nktAWQoiyxmLB5V+foY+LRnPtKtYKXmSGTSXr9TfBrfgeYvLj5a0M2zIEQ24mke1jeKvZSFTFcCRf\nnkloCyFEWaEoOG/dgn5aBNpTJ1FcXDCOfA/ju0EoFb2Ldep1p9Yw9qd30aq1rOj5ES/U/Xuxzlde\nSWgLIUQZoD2wD31UOM6/7kRRqch+eSCGiZOxVq9RrPMqisKMfTHM3h9HRZeKfPTsZzz1WLtinbM8\nk9AWQohSTHP+HPqYqbh88yUAOT17YQgJx9IooNjnNllMjP3pXeLPrKOmZ20+e+5z6lasV+zzlmcS\n2kIIUQqpE2+imxWH69rVqCwWcp9shSFsKrntO5bI/BmmO7y6eTA7rm6jhV9L1jy7Hj/do62pLQpO\nQlsIIUoRVcYd3BbNQ7dkESqjEbN/XQyTIzA917tYbt+6n+uZ1xi4sT8nbx/nb7WfYUmPD9E76Utk\n7vJOQlsIIUoDkwm3j1aimzMD9e3bWPwqY4yMIXvgYHByKrEyTiQfZ+DGF7lhuM6rjV8npuNMuaWr\nBEloCyGEI7Nacfnic/QxUWguX8Tq7oEhOBTjmyNBX7JHt9uvbOO1LYPJMN1hSrsoRjZ/V27pKmES\n2kII4aCcfvoRfVQ4TseOoDg5YRw+AuPo8SiVSv5xoB8d/ojXN76OGjVLe3zI3+u9WOI1CAltIYRw\nONqjh+/evrV9GwDZ/fpjCA7FWvvxEq9FURTmHJhB3N5oKrh48fEzn9KuaocSr0PcJaEthBAOQn3x\nd/SxUbgmbADA1KUrhrBIzE2a2aWeXEsuE3YE8cmpj6lVoRafPLOB+t4N7FKLuEtCWwgh7EyVnIxu\n7gzcVq9ElZtLbtPmGMIiye0caLeaMk0ZDNsyhG1XfqCpb3O2DPkWTZZcIW5vEtpCCGEvBgO6pYtw\nWzgPdWYGllq1MYRMIadPP1Cr7VbWTcMNBm7sz/Hko/So9TeW9lxFFfcqJGVl2K0mcZeEthBClLTc\nXFw/+RjdrFg0txKx+viQETKD7CGvgbOzXUs7nXKKV775P65lXmVIo9eI7TQLrVqiwlHId0IIIUqK\nouD8zVfoYyLRXjiPotNhGDOBrJHvonh42rs6dl7bwdBvB3HHlE7oUxGMahEkt3Q5GAltIYQoAU67\nfkE/NQynA/tRNBqyhg7DMDYYpXJle5cGwIaz8bz349sALO6+gv+r/5KdKxL3I6EthBDFSHPyBPro\nCFy+3wJATu++GELCsPg7xsIaiqIw7+BsYvZMxdO5Ah89s44O1Z62d1niASS0hRCiGKivXoEJM6n4\n0UeoFAVT+453b996srW9S8tjtpqZuGMsa06uorp7DdY9v4EnvBvauyzxEBLaQghhQ6rUFHTz5uC2\ncink5GBpGIAhLAJTt54ltqBHQWTmZjJ8y1C2Xv6OJpWa8clz66mif8zeZYl8SGgLIYQtZGXhtmIp\nuvlzUKenYaleA030NFJ7vgDBd28lAAAgAElEQVQax1pQI9GYyKCN/TmadJiuNbuzoudHuDt72Lss\nUQAFuhEwJiaGl19+mQEDBnD06NH7bjN79mwGDx6c9/rs2bN0796dtWvX5n0tODiY3r17M3jwYAYP\nHsxPP/1UtOqFEMLeLBZcPl2Ld7uWuEdNARVkRkST8usBGDLE4QL7bMoZnv28G0eTDvOPhv9kzTPx\nEtilSL5H2nv37uXSpUvEx8dz4cIFQkJCiI+Pv2eb8+fPs2/fPpz+WB7OaDQSFRVFu3bt/jLemDFj\nCAy031N+hBDCJhQF5+82o4+OQHv6FIqrK8ZRQRjfDUKp4GXv6u5r1/VfGPLtK6TnpDGpTRijnxwn\nt3SVMvkeae/atYvu3bsD4O/vT3p6OpmZmfdsExsbS1BQUN5rZ2dnli9fjp+fn43LFUII+9Pu20OF\nPs9QYfDLaM6eIWvQEFJ2H8IQFumwgf3vcxvo/1UfDLmZLOy2lKBW4yWwS6F8Qzs5OZmKFSvmvfb2\n9iYpKSnvdUJCAm3atKFatWp5X9Nqtbi6ut53vLVr1zJkyBCCgoJISUkpSu1CCFGiNOfO4jl0EBWf\n64Hz7l/J6fUsqT/tInPuQqxVq+U/gB0oisKCQ+/z5vev4aJ15bPnE3ipwSv2Lks8okJfiKYoSt7f\n09LSSEhIYNWqVSQmJua7b58+ffDy8qJhw4YsW7aMhQsXMmXKlAduX7GiDq3Wsc4HPQpf37Jzvqgs\n9QJlqx/ppRhdvw6RkbByJVgs0L49xMXh0rEjLvnsas9ezFYz7377Lov3L6a6Z3U2DdxEk8pNHnk8\nh/u+FEFp7SXf0Pbz8yM5OTnv9a1bt/D19QVg9+7dpKSkMGjQIEwmE5cvXyYmJoaQkJD7jvW/57i7\ndu1KRETEQ+dOTTUWpAeH5uvrQVJS2XjIflnqBcpWP9JL8VDdScdt0Tx0SxahysrCXK8+hskRmJ55\n7u7tW/nUac9eDLkG3vr+NbZc/JZGPo359LkNVFFXfeR6HOn7UlSO3svDfqHI9+PxDh06sGXL3Sf5\nnDhxAj8/P9zd3QHo1asXmzZtYv369SxcuJCAgIAHBjbAqFGjuHLlCgB79uyhXj3HeCKQEELcIycH\nt6WL8G7TDP3cWVg9K5AxZwGp23djevZ5h7rf+s9yLbnsubGbfl8+x5aL39K5eiBf/30zj7lXtXdp\nwgbyPdJu2bIlAQEBDBgwAJVKRXh4OAkJCXh4eNCjR4/77nP8+HHi4uK4du0aWq2WLVu2sGDBAgYN\nGsTo0aNxc3NDp9Mxffp0mzckhBCPzGrFJeFf6GOnobl8CauHJ5mTw8l6YwTodPau7r4UReF82jm2\nX/mRHVd/Yue1n8nMvXsU+coT/2BW53k4aZzsXKWwFZXyvyepHYwjf3xRUI7+MUxhlKVeoGz1I70U\nkaLgtO0H3KPC0Z44huLsTNZrwzGOHovi7fPIwxZXL0nGJHZc3caOqz+x/co2rhuu5b33eIU6dK4e\nSPdaPelRq5fNrhCXn7GS87CPx+WJaEKIck17+CD6qHCcf96OolKR3X8AhomTsdasZe/S8hhzjey+\n8WteSJ+4fSzvPW9Xb/r496NzjUA6Ve9CTU/HqVvYnoS2EKJcUv92AX1sFK5fJABg6tqdzNBILI0f\n/epqW7FYLRxLPsL2K3ePpvfc2IXJagLARePC09W70Ll6IF1qBNK4UlPUqgI93FKUARLaQohyRZWU\nhH52LK4fr0JlNpPbvAWGsKnkPt3ZrnVdunMxL6R/vvoTqTmpee81qdSMTtW70LlGIG0fa4eb1s2O\nlQp7ktAWQpQLqswM3BYvxO2DBagNmVhqP45hcjg5L/zdLleDp2Wn8vO1HX985P0jF+/8nvdeNffq\nPPP483SuEcjT1btQya1SidcnHJOEthCibMvNxXXNavSzYlEnJ2Gt5EtGWCTZg4eCU8ldVZ1jyWH/\nzb3suLqN7Ve2cTjpEFbFCoCHsye9Hn8u7yPvOhXqyiNGxX1JaAshyiZFweWrf6OLmYr299+w6t0x\njJ+EccQo+ONZE8U7vcKxxGN8cewbtl/Zxq7rv2A0331glFatpXWVtnSuHkjnGoG08HsSrVr+cyzy\nJz8lQogyx2nnDvRTw3A6fAhFqyVr2HAMQRNQinkRo5uGG2y/so3tf9yOdcv438c716/YIC+k21ft\nKMthikcioS2EKDM0x4/hPi0c5x+3ApDdtx+G4DCsdfyLZb5MUwa/Xt+ZdyvWmdTTee/5uvkxqMkg\n2vp2pHP1QHkimbAJCW0hRKmnvnwJfew0XD5fj0pRMD3dGUNYJObmLW06j9lq5vCtg2z/47z0/sS9\nmK1mANy0bnSt2Z3O1bvSuUYgDb0b4efn6dAP8RClj4S2EKLUUqXcRjd3Fm6rlqMymTAHNCEzLJLc\nwG42uyL8dtZtvryQwPYr2/jl2s/cMaXfnRsVzf1a5IV0qyptcNHkt+aXEEUjoS2EKH2MRtyWL0Y3\nfy7qjDtYatbCEBxKTr/+oLbNg0YyczNZemQRiw7Nz3uWdy3P2vSt+390rhFIx2pPU9HV2yZzCVFQ\nEtpCiNLDbMb107XoZk5Hc/MGVm9vMqOmkzX0dXCxzVFuriWXNadWM3tfHElZt/Bx9WFsq2k8V6c3\ntSs8bpM5hHhUEtpCCMenKDh/uxF9dATac2dR3NwwBI0ja+R7KJ4VbDKFVbHy1fl/E7NnKhfv/I5O\nq2dsq4m83XwUHs6eNplDiKKS0BZCODTt7l24R03Bad8eFI2GrMGvYhwfjLXKYzabY/uVbUTtDudo\n0mG0ai3Dmgwn6MkJ+OmK9xYxIQpLQlsI4ZA0Z06jj47AZfMmAHKe7Y1hcjiWevVtNseRW4eI2h3B\njqvbAOhX70Umtgnl8Qp1bDaHELYkoS2EcCxXr+I+MQTXzz5BZbWS27YdmVOmYm7d1mZT/JZ+gdg9\nUXxx/u4KX11qdCX0qQia+ja32RxCFAcJbSGEQ1ClpaJb8D4sX4xbdjbmBk9gCI3E1LOXzW7fSjQm\nMmd/HGtOrsZsNdPctwWh7SLpVL2LTcYXorhJaAsh7Cs7G7eVy9DNm4U6LQ2qV+fO+BByXnoFNBqb\nTJFhusOiQ/NYcmQRRrORxyvUYXLbcHr795WFOUSpIqEthLAPiwWXf32GPi4azbWrWCt4kRk2FfdJ\n48jJNNtkihxLDquPr+D9A7O4nX0bP11lItpHM6jhEJw0JbfClxC2IqEthChZioLz1i3op0WgPXUS\nxcUF48j3ML4bhFLRG3c3N8gs2qM/LVYLn59bT9zeaK5kXMbD2ZNJbcIY3uxt9E562/QhhB1IaAsh\nSoz2wD70UeE4/7oTRaUie8AgDBNCsFavYZPxFUXhh8vfEbUrglMpJ3BWO/NWs3d4r+VYfNx8bDKH\nEPYkoS2EKHaa8+fQx0zF5ZsvAcjp2QtDSDiWRgE2m2P/zb1E7Q5n1/VfUKHi5QYDmdAmhBoeNW02\nhxD2JqEthCg26sSb6GbF4bp2NSqLhdwnW2EIm0pu+442m+Nc6lmid0ey6fevAehZqxchT4XTyMd2\nvxAI4SgktIUQNqfKuIPbovnolixEZTRi9q+LISQc0/Mv2Oz2rRuZ15m5bzrrTq/BqlhpVbkNU9pN\n5amq7W0yvhCOSEJbCGE7JhNuH61EN2cG6tu3sfhVxhgZQ/bAweBkm6u107JTWXDofZYfXUy2JZv6\nFRsw+akIetV+Vm7fEmWehLYQouisVly++Bx9TBSayxexuntgCA7F+OZI0Nvmau0scxYrjy1j/sHZ\npOWkUVVfjQltQnipwSto1fKfMlE+yE+6EKJInH76EX1UOE7HjqA4OWEcPgLj6PEolSrZZHyz1cz6\nM58yY28M1w3X8HLxYkq7KIY1GY6b1s0mcwhRWkhoCyEeifbo4bu3b22/u9hGdr/+GIJDsda2zZrT\niqLw7e8bidkTydnUM7hqXBnVIohRLUbj5VrRJnMIUdpIaAshCkV98Xf0sVG4JmwAwNSlK4awSMxN\nmtlsjt3Xf2XqrinsT9yLWqVmcKOhjGsVzGPuVW02hxClkYS2EKJAVMnJ6ObOwG31SlS5ueQ2bY4h\nLJLczoE2m+Pk7RPM/H4aG89tBOC5Oi8Q0nYK9SrabjlOIUozCW0hxMMZDOiWLsJt4TzUmRlYatXG\nEDKFnD79QK22yRRXMi4Ttzeaf535DAWF9lU7EvpUBK2qtLHJ+EKUFRLaQoj7y83F9ZOP0c2KRXMr\nEauPDxkhM8ge8ho4O9tkittZt3n/4CxWHVuOyWqikU9jZv1tBk9W6CC3bwlxHxLaQoh7KQrO33yF\nPiYS7YXzKDodhjETyBr5LoqHp02mMOQaWHbkAxYenkeG6Q41PGoS3CaU/6v/EpX9KpCUVLQFQ4Qo\nqyS0hRB5nH7diX5qGE4HD6BoNGQNHYZhbDBK5cr33V5RFCyKBatizftT+Z+/WxQrVsWK9X+2+eHS\n98zaH8stYyI+rj5M6xDLPxsPw0XjUsLdClH6SGgLUQqZLCaWH13Crus7sSpWNE4qsnNMfwSkFStW\nLFbLnwLz3gD936Ctdz2bCRtT6X4qG4CvmjgT3VPH2UqfY/16w1+C9z9/PiqdVs+YVhMY2fxdPJxt\nc/QuRHkgoS1EKbPz2g4mbh/DubSzD91Oo9KgVqnz/lTnvVajVqlRqdTUTIMJ32fS/0AWagV2+7sy\no7cPx2vrUavUPHaf/fJeqzWoUaNWa1CjuneuP97T5P2pRvXH6yq6x3ij2Qgq6+5/9C6EeDAJbSFK\niVvGW0T8OpkNZ+NRoeK1xm8Q1GoC7k7uVPHz4nayIS8487uIS5Wagm7eHNxWLkWVk4O5YQAZYRH4\nd+vJUrkATAiHJaEthIOzWC18fHIVMXumkp6TRjPfFszsPJfmfi3ztnHVuuKsyc1/sKws3FYsRTd/\nDur0NCzVa2CYOJmcF18GjaYYuxBC2IKEthAO7GjSYcZvH82hWwfxcPZk+tOzGBowDI26kAFrseAa\nvw5dXDSaG9exenmRGRFN1mtvgKtr8RQvhLA5CW0hHNCdnHRi907jw+PLsSpW+tXrT2SHmMKfB1YU\nnL/bjH5aONozp1FcXTG+OwbjqNEoFbyKp3ghRLGR0BbCgSiKwhfnP2fKLyEkGm/i71WXuE5z6FS9\nS6HH0u7bg/vUKTjt2YWiVpM1aAjG8ZOwVq1m+8KFECVCQlsIB/Fb2nkm7BjLjqvbcNW4EtwmlJEt\n3iv0/cuac2fRR0fisulrAHJ6PYdhcjiWBk8UR9lCiBJUoAcHx8TE8PLLLzNgwACOHj16321mz57N\n4MGD816fPXuW7t27s3bt2ryv3bhxg8GDBzNw4EDee+89TCZTEcsXovTLNmcTtzeaTp89xY6r2+hW\nswc7BuxhTKsJhQps9c0buI99j4qd2uKy6WtyW7cl9ast3Pn4UwlsIcqIfEN77969XLp0ifj4eKKj\no4mOjv7LNufPn2ffvn15r41GI1FRUbRr1+6e7ebPn8/AgQNZt24dtWrVYsOGDTZoQYjS68fLW+n0\nWVtm74/Dx60SK/+2hnXPbaB2hYKvSa26kw6TJ+Pdtjlua1ZhqeNP+up1pH3zHean2uU/gBCi1Mg3\ntHft2kX37t0B8Pf3Jz09nczMzHu2iY2NJSgoKO+1s7Mzy5cvx8/P757t9uzZQ7du3QAIDAxk165d\nRW5AiNLoRuZ1Xt/yTwZ8048rGZd5q9k7/PLKPnr79yn4Qhk5ObgtXYR3m2YQE4O1ghcZcxaQun03\npmefB7nfWogyJ99z2snJyQQEBOS99vb2JikpCXd3dwASEhJo06YN1ar99+IWrVaLVvvXobOysnD+\nY3UgHx8fkpKSHjp3xYo6tNrSf++or6+HvUuwmbLUC5R8P2armYV7FxK2LYxMUybtqrdj8XOLaVal\nWcEHsVph3ToIC4OLF8HTE2Ji0Lz3Hh46HWXhO1SWfs6kF8dUWnsp9IVoiqLk/T0tLY2EhARWrVpF\nYmLiI4/zIKmpxsKW53B8fT3KzIpFZakXKPl+9t/cy4QdYziefJSKLhWZ02UBAxsORq1SF6wORcFp\n2w+4R4WjPXEMxdmZrDdHYgwaR6UGte+OYSj935+y9HMmvTgmR+/lYb9Q5Bvafn5+JCcn572+desW\nvr6+AOzevZuUlBQGDRqEyWTi8uXLxMTEEBISct+xdDod2dnZuLq6kpiY+JePz4Uoi1KzU5i2O5K1\nJ1ejoPDKE/8grN1UKrlVKvAY2sMH0UeF4/zzdhSViuz+AzAEh2KtUbMYKxdCOJp8Q7tDhw4sWLCA\nAQMGcOLECfz8/PI+Gu/Vqxe9evUC4OrVq0yaNOmBgQ3Qvn17tmzZQp8+ffjuu+94+umnbdSGEI5H\nURTiz6xj6q4wkrOSecK7ITM6v89TjxX84jD1bxfQx0bh+kUCADndemCYHIGlcZPiKlsI4cDyDe2W\nLVsSEBDAgAEDUKlUhIeHk5CQgIeHBz169LjvPsePHycuLo5r166h1WrZsmULCxYsYNSoUUycOJH4\n+HiqVq1K3759bd6QEI7gdMopJu4Yw67rv6DT6pjSLoo3m76Nk8apQPurkpLQz47F9eNVqMxmclu0\nxBA2ldyOnYq5ciGEI1MpBTm5bCeOfM6hoBz93ElhlKVeoHj6MeQamLN/BouPLMBsNfPM488T3TGO\n6h41CrS/KjMDt8ULcftgAWpDJubH62CYHI6pd9+HXg1elr430otjkl5KTpHOaQshCmbz75uYvHMC\nVzIuU8OjJtOfnknP2s8UbOfcXFzXrEY/KxZ1chLWSr5khEWSPXgoOBXs6FwIUfZJaAtRRFcyLjP5\n5wlsvrgJJ7UT77UcS9CT49E56fLfWVFw+erf6GKmov39N6x6dwzjJ2EcMQr+uHZECCH+Q0JbiEdk\nsphYcmQRc/bHYTQbaV+1IzM6zaW+d4MC7e+0cwf6qWE4HT6EotWSNWw4hqAJKHJXhRDiASS0hXgE\nu67/woTtQZxJPU0lt0rM6DyX/vUHFOhpZprjx3CfFo7zj1sByO7bD0NwGNY6/sVdthCilJPQFqIQ\nkrOSifw1lPgz61Ch4p8Bw5jcdgperhXz3Vd9+RL6uGhcNsSjUhRMT3fGEBaJuXnLEqhcCFEWSGgL\nUQBWxcrakx8xbXc4aTlpNKnUjBmd5/Bk5db57qtKuY1u7izcVi1HZTKR27gphrBIcrt0leeDCyEK\nRUJbiHwcSz7KhO1BHEjch7uTB9Ed43i18Rto1fn838doxG35YnTz56LOuIOlZi0MwaHk9OsP6gKt\niiuEEPeQ0BbiATJNGcTtjWb5sSVYFSt96/ZjaofpVNE/9vAdzWZcP12LbuZ0NDdvYPX2JjNqOllD\nXweXgq+PLYQQfyahLcSfKIrC1xe+IPSXYG4abvB4hTrEPj2bwJrd8tsR5283oo+OQHvuLIqbG4ag\ncWSNfA/Fs0LJFC+EKNMktIX4H7+lX2DSjnFsu/IDLhoXxreexKgWQbhqXR+6n3bPbtynhuG0bw+K\nRkPW4Fcxjg/GWiWfo3IhhCgECW0hgBxLDgsOzmXewdnkWHLoUqMrsU/Poo5X3YfupzlzGn10BC6b\nN90d59neGCaHY6lXvyTKFkKUMxLaolxLzU5hzcmPWHV8Odcyr1JZV4VpHWN5wf/vD73nWn39GrqZ\n03H9dC0qq5Xctu3InDIVc+u2JVi9EKK8kdAW5dLplFOE7l7JmqNryDJnodPqeavZO4xvHYyHs+cD\n91Olp6GbPxe35YtRZWdjfqIhhtAITD16ye1bQohiJ6Etyg2rYmXrpS0sO7qEHVe3AVDToxavNRnO\noIaDqeDi9eCds7Nx+3A5uvdnok5Lw1K1GoaJk8l56RXQaEqoAyFEeSehLcq8TFMGn55ey4pjS/k9\n/TcA2lftyLiOY2jnHYhG/ZDQtVhw+ddn6OOi0Vy7irWCF5lhU8l6/U1wcyuhDoQQ4i4JbVFm/Z7+\nGyuPLWXdqbVk5mbgonHhlSf+wetN36JJpaYPX1NXUXD+4Tv0URFoT51AcXHBOPI9jO8GoVT0LtlG\nhBDiDxLaokxRFIWd13aw7OgHfHdxMwoKlXVVeKfFewwJeI1KbpXyHUN7cD/6qVNw/nUnikpF9oBB\nGCaEYK1eowQ6EEKIB5PQFmVCljmLz8+uZ/nRxZxKOQlAS78neaPpCHr798VZ45zvGJrfzqOPnorL\n118AkNOzF4aQcCyNAoq1diGEKCgJbVGqXc+8xqrjK1hzchUp2Slo1Vr+Xvf/eKPpCFpVaVOgMVSJ\niehnx+K6ZjUqi4XcJ1thCJtKbvuOxVy9EEIUjoS2KHUURWF/4l6WH13M1xe+xKJY8Hb1ZnTLcbza\n+HUec69asIHu3EEXG41uyUJURiNm/7oYQsIxPf+C3L4lhHBIEtqi1DBZTHx14d8sP7qYQ7cOAtDQ\nO4DhTUfQr35/3LQFvJrbZML14w9h7kz0SUlY/CpjjIwhe+BgcHIqxg6EEKJoJLSFw0syJvHxyQ9Z\nfXwlicabqFDRq/azDG/2Nh2qPv3QJ5fdw2rF5YvP0U+PQnPpInh4YJgUhnH426DXF2sPQghhCxLa\nwmEdSz7K8qOL+fe5DeRYcvBw9uTNZiN5rfEbPF6hTqHGctq+DX1UOE5HD6M4OWEcPgLdtEiMPHwh\nECGEcCQS2sKhWKwWvv19I8uPLWbX9V8AqFPBnzeavsXLDQbi7uxRqPG0Rw+jjwrHefvdJ6Bl9+uP\nITgUa+3H0fl6wIPu0xZCCAckoS0cQnpOGmtPfsyHx5dxJeMyAJ2rBzK86Qi61eqJWqUu1HjqSxfR\nT4/CNeFfAJi6dMUQFom5STOb1y6EECVFQlvY1fnUcyw/tpj4059iNBtw07oxpNFrvNH0LRp4P1Ho\n8VTJyejen4nbqhWocnPJbdocQ1gkuZ0Di6F6IYQoWRLaosRZFSs/XfmBZUcX8+PlrQBUc6/O2CYT\n+UfDIVR0fYTHhBoM6JYuwm3hPNSZGVhq1cYQMoWcPv1AXbijdCGEcFQS2qLEZOZmsv7Mp6w4uoTz\naecAaPtYO4Y3HcEzjz+PVv0IP465ubiuW4Nu5nQ0txKx+viQETKD7CGvgXP+T0ETQojSREJbFLvL\ndy6x8tgyPjn1MXdM6TirnXmpwSsMbzqCpr7NH21QRcH5m6/Qx0SivXAeRafHMHYiWW+PQvF48HrY\nQghRmkloi2KhKAq7rv/CsqOL2XxxI1bFiq+bH+NbT+KfAcPw0/k98thOu35BPzUMpwP7UTQasoYO\nwzA2GKVyZRt2IIQQjkdCW9jcl+cTeP/AbE7cPgZAM98WvNH0LfrU7YeLxuWRx9WcPIE+OgKX77cA\nkNO7L4aQMCz+9WxStxBCODoJbWEzJouJsF+CWXV8BRqVhhf8/84bTUfQpkrbgj+17D7UV6+gnxGD\nS/w6VIqCqX3Hu7dvPdnahtULIYTjk9AWNnHLeIvXtwxh941faeTTmA//9jF1vOoWaUxVagq6+XNx\nW7EEVU4O5oYBGMIiMHXrKQt6CCHKJQltUWSHbx1k6LeDuG64Rh//frzfdRF6pyI8yzsrC7cVS9HN\nn4M6PQ1L9RoYJk4m58WXQaOxXeFCCFHKSGiLIll/5lPG/vQuJouJ0KciGdVi9KN/FG6x4LL+U/Rx\n0WiuX8Pq5UVmRDRZr70BrvKMcCGEkNAWj8RsNRO5K4ylRxbh6VyB1b0+oVutno82mKLg/N1m9NER\naE+fQnF1xfjuGIyjRqNU8LJt4UIIUYpJaItCu511m+HfDeXna9upX7EBHz/z6SOfv9bu23N3QY/d\nv6Ko1WQNGoJx/CSsVavZuGohhCj9JLRFoRxPPsbQbwdyOeMSvR5/jkXdluLhXPiHmWjOnUUfHYnL\npq8ByOn1LIaQcCxPNLR1yUIIUWZIaIsCiz8ez6tfvkqWOYvxrScxttXEwq++dfMGupmxuK77GJXF\nQm7rtmSGTcX8VLtiqloIIcoOCW2RL4vVQsyeqSw4NBe9kzsfPfMpzzz+XKHGUN1Jx23RPHRLFqHK\nysJcrz6GyRGYnnlObt8SQogCktAWD5WWncpbW4fx4+Wt1POux4c9Pynckpk5ObitXoFu7kzUKSlY\nqjyGMXoG2QMGgVZ+/IQQojDkv5rigU6nnOKf377C7+m/0a1mDza8sp7cjALeJ2214pLwL/Sx09Bc\nvoTVw5PMyeFkvTECdLriLVwIIcqoAoV2TEwMR44cQaVSERISQtOmTf+yzezZszl8+DBr1qx54D7B\nwcGcOHECL6+7t/EMGzaMLl262K4bYTObfvuGkT8Mx5CbyXstxxLcJhQvVy+SMjIevqOi4LTtB9yj\nwtGeOIbi7IzxrXcwjh6L4u1TMsULIUQZlW9o7927l0uXLhEfH8+FCxcICQkhPj7+nm3Onz/Pvn37\ncHJyynefMWPGEBgYWAytCFuwKlZm7pvO7P1x6LQ6lvdcTZ+6/Qq0r/bwwbu3b/28HUWlIrv/AAwT\nJ2OtWauYqxZCiPIh30t/d+3aRffu3QHw9/cnPT2dzMzMe7aJjY0lKCioUPsIx5NhusPQbwcye38c\nNT1rs7Hf1gIFtvq3C3gMH0rFnl1w/nk7pq7dSf1hJxmLlklgCyGEDeV7pJ2cnExAQEDea29vb5KS\nknB3dwcgISGBNm3aUK1atXz3AVi7di2rVq3Cx8eHsLAwvL29Hzh3xYo6tNrS/6xpX18Pe5eQr7O3\nz/L/7d17VNR1/sfx53AZYGAK0EETxFp/1hpqyrqul21DvG6tty0VhVjLzfwVeC1QQkFN1Mw6ubSd\nzNZScxcrfuWe3HQ3tXYNydWkpHXN2g1Q5OKAMsMwwPD5/UHOygqCOjAz8H6c42nmO9/Pd96vvn7O\ne76Xcaa8N4VT5acYc8cYsh7Kopvu6tPZTbKUlsLq1fDqq1BfD0OHwoYNaKOjaXmvuhZ32DdtJVlc\nk2RxTe6a5bpvRFNK2W3Pa/YAABQnSURBVB9XVlaSnZ3Ntm3bKCkpaXXMlClTCAwMpH///mzZsoXM\nzExWrlzZ4riKiurrLc/lGAx6yspauQ7sZH/5bh+P/3kuVbWXmH9PAitHrKbB7EWZuWndl7NoTFX4\nvZKJ329/g4fZhO32OzA/k4Z18rTGr2+5eN7L3GHftJVkcU2SxTW5epZrfaBotWmHhIRQXl5uf15a\nWorBYADgyJEjGI1GYmNjqa2tpaCggIyMjBbH3HHHHfZl0dHRpKen30ge4SBKKTYff4GM3NX4ePrw\n8pgtTL8rpuUBdXX4/u41/J9fj0d5GQ3dDVStWEXNw3Pg+/sZhBBCtJ9Wr2mPGjWKffv2AZCfn09I\nSIj91PjEiRPZu3cvu3fvJjMzk4iICFJSUlock5iYSGFhIQC5ubn069evvXKJVpjqTPx6/69Ym7uK\nXgGh/HHavpYbtlJo9/wf3H03+mVLwWLB/PRyLnyWR82jj0nDFkKIDtLqkXZkZCQRERHExMSg0WhI\nS0sjOzsbvV7PuHHj2jwGIDY2lkWLFuHn54dOp2PdunWOTSPa5N8X/8Wv/jSbfxjzGdFrFFvHb8eg\nMzS7rvffPsF/zUq8Pz8OXl5Y5s7DvDgJFRLSwVULIYTQqCsvUrsYV77m0Faudu3kUOEB5u2fQ6W1\nkkcHPMaaUevx9rz6SNnz5JcEPJuG9sBfAKiZ+kt8N26g7NYeHV1yu3G1fXMzJItrkiyuydWz3NQ1\nbdE5KKV4JS+T1Tkr8NJ48WJUJrF3x1+1nkfBd/hvWIvPO1lolKL23vswr1hF/eBIfA16t7nJTAgh\nOiNp2l2Apd7CkoOJvPv1bnroerJt4k6G9hzWZB2N8QK6F5/Hb9traGprqRswCPOKVdRFRcsPeggh\nhIuQpt3JFVUVMufDWL4oO8GPevyYbRN30tP/tv+sUF2N32uvoNv8Ih5Vl7CF98G8LBXrL6eDx/X9\n7KYQQoj2JU27E/v07N/49f54yi3lxPaPZ/3PNuHj6dP4Yn09vr/fiW7jOjzPF9MQHIxpzTosc34N\nPj7OLVwIIUSzpGl3QkopfndyCysOLwdgw89eYE7EXDQaTePXt/70Af5r0/H6+jTKzw/z4qewPLkQ\ndcutTq5cCCHEtUjT7mRq6mtY9slSdp3aQXc/A7+bsIPhvUYC4HUkh4A1K/E+movy9MTy8CNUP72M\nhp63tbJVIYQQrkCadidSbDrHo/viOFbyd+4xDOGNiW8Rqg/D85+n8F+bjs+HewGw3j8J8zNp2Prd\n6eSKhRBCXA9p2p3EZ8W5PLovjtLqEqbfGcPzUS/hX2pEtzIB39/vRNPQQN1PRmBauZr6H//E2eUK\nIYS4AdK0O4GdX71J8idLaFANrBm1jsf7zMZ/3Xr8XnsFTU0N9T/sjzk1ndpxE+XrW0II4cakabux\nWlstqX9L5o381wnyCeL1qNcYt++f6Kbfg0dlJbZeoZiTn8E6YxZ4uv9PnAohRFcnTdtNlVaXMnff\nw+QW5zAgKII91hjCH1qE59kiGm4NxLRyDZa588DPz9mlCiGEcBBp2m7o85JjzPkwlmLTOVabRpKc\nVYH2HytQPj5UP7mQ6gWLUUHBzi5TCCGEg0nTdjNZp3bx1McLGfydlcO5t3PHl5+iNBoss+KoTkqh\nITTM2SUKIYRoJ9K03UR9Qz2rPk3lwIHf8odDXkw9CfBvrOMnYn4mHVv/u51dohBCiHYmTdsNXLBc\nYPnuWYzPOkLmcfBqqKfuR0Mxr1hN3cifOrs8IYQQHUSatgurs9Vx8l9/5au0eHYeuoR/HdT+4Adc\nTF1N7QOT5OtbQgjRxUjTdiJznZmiqkKKqgoorCpsfGxq/G9JRQGTPykm9WPF+Gq4FOTPpZRnsc6O\nB29vZ5cuhBDCCaRptxOlFMYaIwXnTvNFwSmKTAUUVRVSWFXIWVMRRVUFGGuMV43TNMCsrzTsPuhB\nnwuKaj8vvpw/nZ7JL4C/vxOSCCGEcBXStG9QfUM9583FFH3fgC835MuPz5qKqK6vbnasn5cfoQFh\nDDIMprc+nLCA3oTpezM4v5zBv9mJLv8rlLcH1fPmUb3oaXp2797B6YQQQrgiadotsNRbOFtVRGFV\nAUWmQs5ebsrfn74+ZzqLTdmaHRvkE8QPAv+HMH1v7jT0pZtXT8L0vemt701oQG+6+3Vv/JnM73l9\ncQL/1DS0Hx8EoObBGZiXpdLQ5/aOiCqEEMJNdMmmrZTiorWSwu8b8JXXlM+aGptzuaWs2bEaNPT0\nv43IHkMJCwgjTB9ub8hh+nDCAsII0Ort6xsMesrKqprdlse//4X/+mfxzX4bgNqoaMwrVlE/8B7H\nhxZCCOH2ukzTblANLDmYyPHSv1NUVYSprvlGqvXQEqoPo3+3CHp/f9ra/iegN70CQtF6am+qFk15\nOboXn8PvjdfR1NVRN2gw5hWrqLtv9E1tVwghROfWZZp2TX0NhwoPUFVXRW99+PdHxo1Hx42nrcPo\nrQ/HoAvBQ+PRPkWYzehefRm/zJfwMFVh63M75pSVWKf8Ejza6T2FEEJ0Gl2maeu8dXwe/1WTa8kd\npq4O37e2o3t+PZ6lJTR060ZVynPUxD8K2ps7ahdCCNF1dJmmDXR8w1YK3n2XoORleH1zBqXzx7w0\nGcsTiSj9LR1bixBCCLfXpZp2R/LOOYz/6hVw7O94enpimTMX89JlqB49nF2aEEIINyVN28E8v8rH\nf206Pn/e17hg+nQqlizD1refcwsTQgjh9qRpO4hHUSH+z2Xgk7ULjVLUjvwp5pWrCZowGlsLX/kS\nQgghroc07ZukqTCie+kF/F5/FY3VSn3/CMwrV1EbPU5+0EMIIYRDSdO+URYLfltfRbf5BTwuVmIL\n6405+RmsD80ET09nVyeEEKITkqZ9vWw2fLN2oduwFs/iczQEBmJKX4vl0cfA19fZ1QkhhOjEpGm3\nlVJo93+I/7NpeP3zFMrXl+oFS6hOXIS6NdDZ1QkhhOgCpGm3gdfRXPzXpKE98inKwwNLbDzVTy+n\noVeos0sTQgjRhUjTvgbPr0/jv3YVPnv/CIB14gOYn0nDdtcPnVyZEEKIrkiadjM8zhej27ge313b\n0dhs1P34J5hWrKZ++AhnlyaEEKILk6Z9Bc2li/hlvoTu1ZfRWCzU97sTc+oqaifeL1/fEkII4XTS\ntAGsVvze2IruxY14GI3Yet5G9drnqImJBS/5XySEEMI1dO2O1NCAz7u78V//LJ6FBTTob8H0TBqW\nx/4XdDpnVyeEEEI00TWbtlJ4H/yIgDVpeOV/idJqqZ6fQPWipajgbs6uTgghhGhWl2vaXieON359\n668fozQaaqbHYF6WSkPvcGeXJoQQQlxT12naNhv6xQn4/uEtAKxjxmF+Jh3bgIFOLkwIIYRomzY1\n7YyMDPLy8tBoNKSkpDBo0KCr1tm0aRMnTpxgx44dLY4pLi4mKSkJm82GwWBg48aNaLVaxyZqidWK\ndt9e6oZEYl6xmrqf/qxj3lcIIYRwEI/WVvjss8/47rvvyMrKYu3ataxdu/aqdc6cOcPRo0dbHbN5\n82Zmz57Nrl276NOnD++8844Do7RCp+NC/jdU7jskDVsIIYRbarVp5+TkMHbsWAD69u3LxYsXMZlM\nTdZZv349ixcvbnVMbm4uY8aMAWD06NHk5OQ4LEibyNe3hBBCuLFWm3Z5eTlBQUH258HBwZSVldmf\nZ2dnM2zYMEJDQ1sdY7FY7KfDu3Xr1mQ7QgghhLi26z70VErZH1dWVpKdnc22bdsoKSlp05hrLftv\nQUE6vLzc/7epDQa9s0twmM6UBTpXHsnimiSLa3LXLK027ZCQEMrLy+3PS0tLMRgMABw5cgSj0Uhs\nbCy1tbUUFBSQkZHR4hidTkdNTQ2+vr6UlJQQEhJyzfeuqKi+0Vwuw2DQU1ZW5ewyHKIzZYHOlUey\nuCbJ4ppcPcu1PlC0enp81KhR7Nu3D4D8/HxCQkIICAgAYOLEiezdu5fdu3eTmZlJREQEKSkpLY4Z\nOXKkffn+/fu59957bzqcEEII0VW0eqQdGRlJREQEMTExaDQa0tLSyM7ORq/XM27cuDaPAUhMTCQ5\nOZmsrCx69erF1KlTHZtGCCGE6MQ0qi0Xl53ElU9ftJWrn4a5Hp0pC3SuPJLFNUkW1+TqWW7q9LgQ\nQgghXIM0bSGEEMJNSNMWQggh3IQ0bSGEEMJNSNMWQggh3IRL3z0uhBBCiP+QI20hhBDCTUjTFkII\nIdyENG0hhBDCTUjTFkIIIdyENG0hhBDCTUjTFkIIIdxEq7/yJRplZGSQl5eHRqMhJSWFQYMGXbXO\npk2bOHHiBDt27CA3N5eFCxfSr18/AO68805WrFhBcXExy5cvp76+Hi8vLzZu3IjBYCAiIoLIyEj7\ntt544w08PT1dOsuyZcvIz88nMDAQgLlz5xIVFcWePXt488038fDwYMaMGUyfPr1dcjg6z4IFC6io\nqACgsrKSwYMH8/jjjzNp0iQGDBgAQFBQEJs3b3aZLAB79uxh69ateHl5sWDBAqKioiguLiYpKQmb\nzYbBYGDjxo1otdoO3TeOzOJuc6alLK4wZxyVxR3ny9tvv82ePXvsr508eZLPP/+cU6dOkZ6eDsBd\nd93FqlWrANi6dSsffvghGo2GhIQE7rvvvnbL0mZKtCo3N1fNmzdPKaXUmTNn1IwZM65a5+uvv1Yz\nZ85UcXFxSimljhw5ohITE69aLykpSX3wwQdKKaV27typNmzYoJRSatiwYe1VfhOOzJKcnKwOHDjQ\nZJnZbFbjx49Xly5dUhaLRT3wwAOqoqKiHZI0cmSeKy1btkzl5eWpwsJCNW3aNMcX3owbyWI0GtX4\n8eNVVVWVKikpUampqfb69+7dq5RSatOmTeqtt97q0H3jyCzuOGdayuLsOePILFdyl/ny3+PT09OV\nUkrFxcWpvLw8pZRSS5YsUYcOHVIFBQVq2rRpymq1qgsXLqgJEyao+vr6dkzUNnJ6vA1ycnIYO3Ys\nAH379uXixYuYTKYm66xfv57Fixe3uq20tDQmTJgANH4KraysdHzB1+DILM3Jy8tj4MCB6PV6fH19\niYyM5Pjx4zddd0vaI8+3335LVVVVs5/a29ONZMnJyWHEiBEEBAQQEhLCmjVrAMjNzWXMmDEAjB49\nmpycnA7dN47M4o5zpqUszXHX/XKZO82XK7388ss88cQT1NbWcvbsWXv9l+dLbm4u9957L1qtluDg\nYEJDQzlz5kz7hmoDadptUF5eTlBQkP15cHAwZWVl9ufZ2dkMGzaM0NDQJuPOnDnD/PnzmTVrFocP\nHwZAp9Ph6emJzWZj165dTJo0CYDa2lqWLl1KTEwM27Ztc4ssADt37iQ+Pp7FixdjNBopLy8nODi4\nxe27eh6A7du3ExcX1+Q9FixYQExMTJNTa452I1mKioqoqalh/vz5zJ49m5ycHAAsFgtarRaAbt26\nUVZW1qH7xpFZ3HHOtJQFnDtnHJ0F3Gu+XPbFF19w2223YTAYqKio4JZbbrG/5oz5cj3kmvYNUFf8\ny6+VlZVkZ2ezbds2SkpK7Mtvv/12EhIS+PnPf05hYSHx8fHs378frVaLzWYjKSmJ4cOHM2LECACS\nkpKYPHkyGo2GuLg4hg4dysCBA106y5QpUwgMDKR///5s2bKFzMxMhgwZ0uL2O8LN7pva2lqOHTtm\nv74VGBjIwoULmTx5MlVVVUyfPp3hw4cTEhLiElkuv5aZmcm5c+eIj4/n4MGDLW6nLcvbw81k0Wg0\nbjdnWsrianPmZveLO84XgHfeeYdp06a1up22LO9ocqTdBiEhIZSXl9ufl5aWYjAYADhy5AhGo5HY\n2FgSEhLIz88nIyODHj16cP/996PRaAgPD6d79+72vzzLly+nT58+JCQk2Lc5a9Ys/P390el0DB8+\nnNOnT7t8lhEjRtC/f38AoqOjOX36dLPbb88J6+h9c/To0San+QICAnjwwQfx9vYmODiYAQMG8O23\n37pMlm7dujFkyBC8vLwIDw/H398fo9GITqejpqYGgJKSEkJCQjp03zgyC7jfnGkpi7PnjKP3i7vN\nl8tyc3PtH5aCg4ObXHJpab5cXu50zriQ7m6OHTum5syZo5RS6uTJkyomJqbZ9QoLC+03PLz//vtq\n69atSimlSktLVVRUlLJarer9999XKSkpTcZ98803asmSJaqhoUHV1dWpmTNn2m+KcOUsCQkJqqCg\nQCnVeINQenq6slgsauzYserixYvKZDLZb7BpL47Mo5RSr7zyitq+fbt9XE5OjsrIyFBK/eeGofPn\nz7tMlvPnz6s5c+Yom82mjEajioqKUjabTaWmpqr33ntPKaXUmjVr1O7duzt03zgyizvOmZayOHvO\nODKLUu43Xy7n+e+b5R555BF19OhRpZRS8+fPV4cPH1Znz55Vv/jFL5TValXnz59X48ePt+d2Jjk9\n3gaRkZFEREQQExODRqMhLS2N7Oxs9Ho948aNa3ZMdHQ0Tz31FB999BF1dXWkp6ej1WrZtWsXVquV\nhx9+GGi8gSI9PZ2ePXvy0EMP4eHhQXR0dLvd1OHILLGxsSxatAg/Pz90Oh3r1q3D19eXpUuXMnfu\nXDQaDU8++SR6vb5dsjg6D0BZWRnh4eH2dYcOHcp7773HzJkzsdlszJs3jx49erhMlh49ejBhwgRm\nzJgBQGpqKh4eHiQmJpKcnExWVha9evVi6tSpeHt7d9i+cWQWd5wzLWVx9pxxZBZwv/lyueYrr1UD\npKSksHLlShoaGrjnnnsYOXIkADNmzCAuLg6NRkN6ero9tzPJT3MKIYQQbsL5HxuEEEII0SbStIUQ\nQgg3IU1bCCGEcBPStIUQQgg3IU1bCCGEcBPStIUQQgg3IU1bCCGEcBPStIUQQgg38f/Ga4I9ntCS\nBgAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {
+ "tags": []
+ }
+ }
+ ]
+ },
+ {
+ "metadata": {
+ "id": "Kwo3QZWWT-zZ",
+ "colab_type": "code",
+ "colab": {}
+ },
+ "cell_type": "code",
+ "source": [
+ ""
+ ],
+ "execution_count": 0,
+ "outputs": []
+ }
+ ]
+}
\ No newline at end of file