Skip to content

Latest commit

 

History

History
594 lines (496 loc) · 15.2 KB

README_EN.md

File metadata and controls

594 lines (496 loc) · 15.2 KB
comments difficulty edit_url tags
true
Easy
Depth-First Search
Breadth-First Search
Union Find
Graph

1971. Find if Path Exists in Graph

中文文档

Description

There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

You want to determine if there is a valid path that exists from vertex source to vertex destination.

Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise.

 

Example 1:

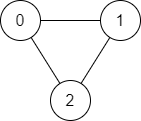
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2

Example 2:

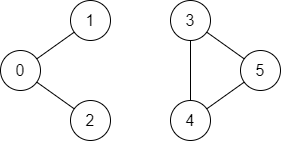
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.

 

Constraints:

  • 1 <= n <= 2 * 105
  • 0 <= edges.length <= 2 * 105
  • edges[i].length == 2
  • 0 <= ui, vi <= n - 1
  • ui != vi
  • 0 <= source, destination <= n - 1
  • There are no duplicate edges.
  • There are no self edges.

Solutions

Solution 1: DFS

First, we convert edges into an adjacency list $g$, then use DFS to determine whether there is a path from source to destination.

During the process, we use an array vis to record the vertices that have been visited to avoid repeated visits.

The time complexity is $O(n + m)$, and the space complexity is $O(n + m)$. Where $n$ and $m$ are the number of nodes and edges, respectively.

Python3

class Solution:
    def validPath(
        self, n: int, edges: List[List[int]], source: int, destination: int
    ) -> bool:
        def dfs(i):
            if i == destination:
                return True
            vis.add(i)
            for j in g[i]:
                if j not in vis and dfs(j):
                    return True
            return False

        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        vis = set()
        return dfs(source)

Java

class Solution {
    private int destination;
    private boolean[] vis;
    private List<Integer>[] g;

    public boolean validPath(int n, int[][] edges, int source, int destination) {
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        vis = new boolean[n];
        this.destination = destination;
        return dfs(source);
    }

    private boolean dfs(int i) {
        if (i == destination) {
            return true;
        }
        vis[i] = true;
        for (int j : g[i]) {
            if (!vis[j] && dfs(j)) {
                return true;
            }
        }
        return false;
    }
}

C++

class Solution {
public:
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        vector<bool> vis(n);
        vector<int> g[n];
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].emplace_back(b);
            g[b].emplace_back(a);
        }
        function<bool(int)> dfs = [&](int i) -> bool {
            if (i == destination) {
                return true;
            }
            vis[i] = true;
            for (int& j : g[i]) {
                if (!vis[j] && dfs(j)) {
                    return true;
                }
            }
            return false;
        };
        return dfs(source);
    }
};

Go

func validPath(n int, edges [][]int, source int, destination int) bool {
	vis := make([]bool, n)
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	var dfs func(int) bool
	dfs = func(i int) bool {
		if i == destination {
			return true
		}
		vis[i] = true
		for _, j := range g[i] {
			if !vis[j] && dfs(j) {
				return true
			}
		}
		return false
	}
	return dfs(source)
}

TypeScript

function validPath(n: number, edges: number[][], source: number, destination: number): boolean {
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }

    const vis = new Set<number>();
    const dfs = (i: number) => {
        if (i === destination) {
            return true;
        }
        if (vis.has(i)) {
            return false;
        }

        vis.add(i);
        return g[i].some(dfs);
    };

    return dfs(source);
}

Rust

use std::collections::HashSet;

impl Solution {
    pub fn valid_path(n: i32, edges: Vec<Vec<i32>>, source: i32, destination: i32) -> bool {
        let mut vis = vec![false; n as usize];
        let mut g = vec![HashSet::new(); n as usize];

        for e in edges {
            let a = e[0] as usize;
            let b = e[1] as usize;
            g[a].insert(b);
            g[b].insert(a);
        }

        dfs(source as usize, destination as usize, &mut vis, &g)
    }
}

fn dfs(i: usize, destination: usize, vis: &mut Vec<bool>, g: &Vec<HashSet<usize>>) -> bool {
    if i == destination {
        return true;
    }
    vis[i] = true;
    for &j in &g[i] {
        if !vis[j] && dfs(j, destination, vis, g) {
            return true;
        }
    }
    false
}

Solution 2: BFS

We can also use BFS to determine whether there is a path from source to destination.

Specifically, we define a queue $q$ and initially add source to the queue. In addition, we use a set vis to record the vertices that have been visited to avoid repeated visits.

Next, we continuously take out the vertex $i$ from the queue. If $i = \text{destination}$, it means that there is a path from source to destination, and we return true. Otherwise, we traverse all adjacent vertices $j$ of $i$. If $j$ has not been visited, we add $j$ to the queue $q$ and mark $j$ as visited.

Finally, if the queue is empty, it means that there is no path from source to destination, and we return false.

The time complexity is $O(n + m)$, and the space complexity is $O(n + m)$. Where $n$ and $m$ are the number of nodes and edges, respectively.

Python3

class Solution:
    def validPath(
        self, n: int, edges: List[List[int]], source: int, destination: int
    ) -> bool:
        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)

        q = deque([source])
        vis = {source}
        while q:
            i = q.popleft()
            if i == destination:
                return True
            for j in g[i]:
                if j not in vis:
                    vis.add(j)
                    q.append(j)
        return False

Java

class Solution {
    public boolean validPath(int n, int[][] edges, int source, int destination) {
        List<Integer>[] g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        Deque<Integer> q = new ArrayDeque<>();
        q.offer(source);
        boolean[] vis = new boolean[n];
        vis[source] = true;
        while (!q.isEmpty()) {
            int i = q.poll();
            if (i == destination) {
                return true;
            }
            for (int j : g[i]) {
                if (!vis[j]) {
                    vis[j] = true;
                    q.offer(j);
                }
            }
        }
        return false;
    }
}

C++

class Solution {
public:
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        queue<int> q{{source}};
        vector<bool> vis(n);
        vis[source] = true;
        while (q.size()) {
            int i = q.front();
            q.pop();
            if (i == destination) {
                return true;
            }
            for (int j : g[i]) {
                if (!vis[j]) {
                    vis[j] = true;
                    q.push(j);
                }
            }
        }
        return false;
    }
};

Go

func validPath(n int, edges [][]int, source int, destination int) bool {
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	q := []int{source}
	vis := make([]bool, n)
	vis[source] = true
	for len(q) > 0 {
		i := q[0]
		q = q[1:]
		if i == destination {
			return true
		}
		for _, j := range g[i] {
			if !vis[j] {
				vis[j] = true
				q = append(q, j)
			}
		}
	}
	return false
}

TypeScript

function validPath(n: number, edges: number[][], source: number, destination: number): boolean {
    const g: number[][] = Array.from({ length: n }, () => []);

    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }

    const vis = new Set<number>();
    const q = [source];

    while (q.length) {
        const i = q.pop()!;
        if (i === destination) {
            return true;
        }
        if (vis.has(i)) {
            continue;
        }
        vis.add(i);
        q.push(...g[i]);
    }

    return false;
}

Rust

use std::collections::{ HashSet, VecDeque };

impl Solution {
    pub fn valid_path(n: i32, edges: Vec<Vec<i32>>, source: i32, destination: i32) -> bool {
        let mut g = vec![HashSet::new(); n as usize];
        for e in edges {
            let a = e[0] as usize;
            let b = e[1] as usize;
            g[a].insert(b);
            g[b].insert(a);
        }

        let mut q = VecDeque::new();
        q.push_back(source as usize);
        let mut vis = vec![false; n as usize];
        vis[source as usize] = true;

        while let Some(i) = q.pop_front() {
            if i == (destination as usize) {
                return true;
            }
            for &j in &g[i] {
                if !vis[j] {
                    vis[j] = true;
                    q.push_back(j);
                }
            }
        }

        false
    }
}

Solution 3: Union-Find

Union-Find is a tree-like data structure that, as the name suggests, is used to handle some disjoint set merge and query problems. It supports two operations:

  1. Find: Determine which subset an element belongs to. The time complexity of a single operation is $O(\alpha(n))$.
  2. Union: Merge two subsets into one set. The time complexity of a single operation is $O(\alpha(n))$.

For this problem, we can use the Union-Find set to merge the edges in edges, and then determine whether source and destination are in the same set.

The time complexity is $O(n \log n + m)$ or $O(n \alpha(n) + m)$, and the space complexity is $O(n)$. Where $n$ and $m$ are the number of nodes and edges, respectively.

Python3

class Solution:
    def validPath(
        self, n: int, edges: List[List[int]], source: int, destination: int
    ) -> bool:
        def find(x):
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        p = list(range(n))
        for u, v in edges:
            p[find(u)] = find(v)
        return find(source) == find(destination)

Java

class Solution {
    private int[] p;

    public boolean validPath(int n, int[][] edges, int source, int destination) {
        p = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
        for (int[] e : edges) {
            p[find(e[0])] = find(e[1]);
        }
        return find(source) == find(destination);
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

C++

class Solution {
public:
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        vector<int> p(n);
        iota(p.begin(), p.end(), 0);
        function<int(int)> find = [&](int x) -> int {
            if (p[x] != x) {
                p[x] = find(p[x]);
            }
            return p[x];
        };
        for (auto& e : edges) {
            p[find(e[0])] = find(e[1]);
        }
        return find(source) == find(destination);
    }
};

Go

func validPath(n int, edges [][]int, source int, destination int) bool {
	p := make([]int, n)
	for i := range p {
		p[i] = i
	}
	var find func(x int) int
	find = func(x int) int {
		if p[x] != x {
			p[x] = find(p[x])
		}
		return p[x]
	}
	for _, e := range edges {
		p[find(e[0])] = find(e[1])
	}
	return find(source) == find(destination)
}

TypeScript

function validPath(n: number, edges: number[][], source: number, destination: number): boolean {
    const p: number[] = Array.from({ length: n }, (_, i) => i);
    const find = (x: number): number => {
        if (p[x] !== x) {
            p[x] = find(p[x]);
        }
        return p[x];
    };
    for (const [a, b] of edges) {
        p[find(a)] = find(b);
    }
    return find(source) === find(destination);
}