comments

difficulty

edit_url

rating

source

2920. 收集所有金币可获得的最大积分

题目描述

有一棵由 n 个节点组成的无向树，以 0 为根节点，节点编号从 0 到 n - 1 。给你一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [a_i, b_i] 表示在树上的节点 a_i 和 b_i 之间存在一条边。另给你一个下标从 0 开始、长度为 n 的数组 coins 和一个整数 k ，其中 coins[i] 表示节点 i 处的金币数量。

从根节点开始，你必须收集所有金币。要想收集节点上的金币，必须先收集该节点的祖先节点上的金币。

节点 i 上的金币可以用下述方法之一进行收集：

收集所有金币，得到共计 coins[i] - k 点积分。如果 coins[i] - k 是负数，你将会失去 abs(coins[i] - k) 点积分。
收集所有金币，得到共计 floor(coins[i] / 2) 点积分。如果采用这种方法，节点 i 子树中所有节点 j 的金币数 coins[j] 将会减少至 floor(coins[j] / 2) 。

返回收集所有树节点的金币之后可以获得的最大积分。

示例 1：

输入：edges = [[0,1],[1,2],[2,3]], coins = [10,10,3,3], k = 5
输出：11                        
解释：
使用第一种方法收集节点 0 上的所有金币。总积分 = 10 - 5 = 5 。
使用第一种方法收集节点 1 上的所有金币。总积分 = 5 + (10 - 5) = 10 。
使用第二种方法收集节点 2 上的所有金币。所以节点 3 上的金币将会变为 floor(3 / 2) = 1 ，总积分 = 10 + floor(3 / 2) = 11 。
使用第二种方法收集节点 3 上的所有金币。总积分 =  11 + floor(1 / 2) = 11.
可以证明收集所有节点上的金币能获得的最大积分是 11 。

示例 2：

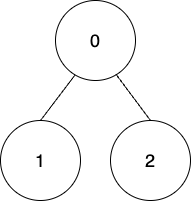
输入：edges = [[0,1],[0,2]], coins = [8,4,4], k = 0
输出：16
解释：
使用第一种方法收集所有节点上的金币，因此，总积分 = (8 - 0) + (4 - 0) + (4 - 0) = 16 。

提示：

n == coins.length
2 <= n <= 10⁵
0 <= coins[i] <= 10⁴
edges.length == n - 1
0 <= edges[i][0], edges[i][1] < n
0 <= k <= 10⁴

解法

方法一：记忆化搜索

我们先根据题目给定的边构建图 $g$，其中 $g[i]$ 表示节点 $i$ 的所有邻接节点。然后我们可以使用记忆化搜索的方法求解本题。

我们设计一个函数 $dfs(i, fa, j)$，表示当前节点为 $i$，父节点为 $fa$，当前节点的金币数需要右移 $j$ 位，所能获得的最大积分。

函数 $dfs(i, fa, j)$ 的执行过程如下：

如果我们使用第一种方法收集当前节点的金币，那么当前节点的积分为 $(coins[i] >> j) - k$，然后我们遍历当前节点的所有邻接节点 $c$，如果 $c$ 不等于 $fa$，那么我们将 $dfs(c, i, j)$ 的结果累加到当前节点的积分中。

如果我们使用第二种方法收集当前节点的金币，那么当前节点的积分为 $coins[i] >> (j + 1)$，然后我们遍历当前节点的所有邻接节点 $c$，如果 $c$ 不等于 $fa$，那么我们将 $dfs(c, i, j + 1)$ 的结果累加到当前节点的积分中。注意，由于题目中给定的 $coins[i]$ 最大值为 $10^4$，因此我们最多只能右移 $14$ 位，就使得 $coins[i] >> (j + 1)$ 的值为 $0$。

最后，我们返回当前节点使用两种方法中能获得的最大积分。

为了避免重复计算，我们使用记忆化搜索的方法，将 $dfs(i, fa, j)$ 的结果存储到 $f[i][j]$ 中，其中 $f[i][j]$ 表示当前节点为 $i$，父节点为 $fa$，当前节点的金币数需要右移 $j$ 位，所能获得的最大积分。

时间复杂度 $O(n \times \log M)$，空间复杂度 $O(n \times \log M)$。其中 $M$ 表示 $coins[i]$ 的最大值。

Python3

class Solution:
    def maximumPoints(self, edges: List[List[int]], coins: List[int], k: int) -> int:
        @cache
        def dfs(i: int, fa: int, j: int) -> int:
            a = (coins[i] >> j) - k
            b = coins[i] >> (j + 1)
            for c in g[i]:
                if c != fa:
                    a += dfs(c, i, j)
                    if j < 14:
                        b += dfs(c, i, j + 1)
            return max(a, b)

        n = len(coins)
        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        ans = dfs(0, -1, 0)
        dfs.cache_clear()
        return ans

Java

class Solution {
    private int k;
    private int[] coins;
    private Integer[][] f;
    private List<Integer>[] g;

    public int maximumPoints(int[][] edges, int[] coins, int k) {
        this.k = k;
        this.coins = coins;
        int n = coins.length;
        f = new Integer[n][15];
        g = new List[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        return dfs(0, -1, 0);
    }

    private int dfs(int i, int fa, int j) {
        if (f[i][j] != null) {
            return f[i][j];
        }
        int a = (coins[i] >> j) - k;
        int b = coins[i] >> (j + 1);
        for (int c : g[i]) {
            if (c != fa) {
                a += dfs(c, i, j);
                if (j < 14) {
                    b += dfs(c, i, j + 1);
                }
            }
        }
        return f[i][j] = Math.max(a, b);
    }
}

C++

class Solution {
public:
    int maximumPoints(vector<vector<int>>& edges, vector<int>& coins, int k) {
        int n = coins.size();
        int f[n][15];
        memset(f, -1, sizeof(f));
        vector<int> g[n];
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].emplace_back(b);
            g[b].emplace_back(a);
        }
        function<int(int, int, int)> dfs = [&](int i, int fa, int j) {
            if (f[i][j] != -1) {
                return f[i][j];
            }
            int a = (coins[i] >> j) - k;
            int b = coins[i] >> (j + 1);
            for (int c : g[i]) {
                if (c != fa) {
                    a += dfs(c, i, j);
                    if (j < 14) {
                        b += dfs(c, i, j + 1);
                    }
                }
            }
            return f[i][j] = max(a, b);
        };
        return dfs(0, -1, 0);
    }
};

Go

func maximumPoints(edges [][]int, coins []int, k int) int {
	n := len(coins)
	f := make([][]int, n)
	for i := range f {
		f[i] = make([]int, 15)
		for j := range f[i] {
			f[i][j] = -1
		}
	}
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	var dfs func(int, int, int) int
	dfs = func(i, fa, j int) int {
		if f[i][j] != -1 {
			return f[i][j]
		}
		a := (coins[i] >> j) - k
		b := coins[i] >> (j + 1)
		for _, c := range g[i] {
			if c != fa {
				a += dfs(c, i, j)
				if j < 14 {
					b += dfs(c, i, j+1)
				}
			}
		}
		f[i][j] = max(a, b)
		return f[i][j]
	}
	return dfs(0, -1, 0)
}

TypeScript

function maximumPoints(edges: number[][], coins: number[], k: number): number {
    const n = coins.length;
    const f: number[][] = Array.from({ length: n }, () => Array(15).fill(-1));
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    const dfs = (i: number, fa: number, j: number): number => {
        if (f[i][j] !== -1) {
            return f[i][j];
        }
        let a = (coins[i] >> j) - k;
        let b = coins[i] >> (j + 1);
        for (const c of g[i]) {
            if (c !== fa) {
                a += dfs(c, i, j);
                if (j < 14) {
                    b += dfs(c, i, j + 1);
                }
            }
        }
        return (f[i][j] = Math.max(a, b));
    };
    return dfs(0, -1, 0);
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

README.md

README.md

2920. 收集所有金币可获得的最大积分

题目描述

解法

方法一：记忆化搜索

Python3

Java

C++

Go

TypeScript

Files

README.md

Latest commit

History

README.md

File metadata and controls

2920. 收集所有金币可获得的最大积分

题目描述

解法

方法一：记忆化搜索

Python3

Java

C++

Go

TypeScript