Skip to content

Latest commit

 

History

History
267 lines (224 loc) · 9.37 KB

README_EN.md

File metadata and controls

267 lines (224 loc) · 9.37 KB
comments difficulty edit_url rating source tags
true
Medium
1939
Weekly Contest 370 Q3
Tree
Depth-First Search
Dynamic Programming

2925. Maximum Score After Applying Operations on a Tree

中文文档

Description

There is an undirected tree with n nodes labeled from 0 to n - 1, and rooted at node 0. You are given a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

You are also given a 0-indexed integer array values of length n, where values[i] is the value associated with the ith node.

You start with a score of 0. In one operation, you can:

  • Pick any node i.
  • Add values[i] to your score.
  • Set values[i] to 0.

A tree is healthy if the sum of values on the path from the root to any leaf node is different than zero.

Return the maximum score you can obtain after performing these operations on the tree any number of times so that it remains healthy.

 

Example 1:

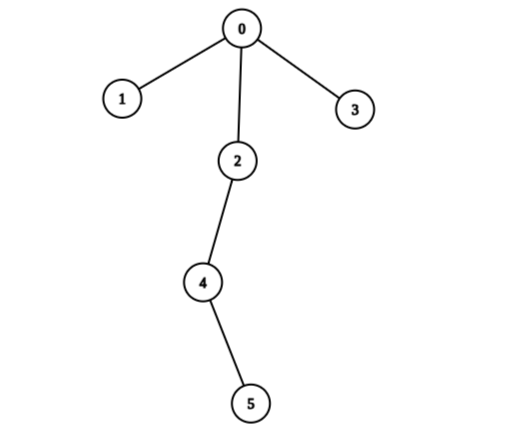
Input: edges = [[0,1],[0,2],[0,3],[2,4],[4,5]], values = [5,2,5,2,1,1]
Output: 11
Explanation: We can choose nodes 1, 2, 3, 4, and 5. The value of the root is non-zero. Hence, the sum of values on the path from the root to any leaf is different than zero. Therefore, the tree is healthy and the score is values[1] + values[2] + values[3] + values[4] + values[5] = 11.
It can be shown that 11 is the maximum score obtainable after any number of operations on the tree.

Example 2:

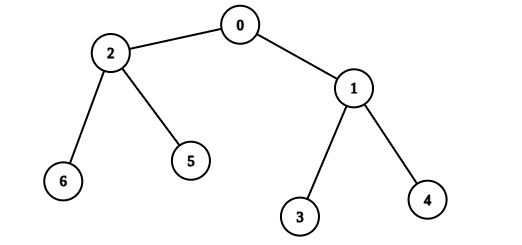
Input: edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], values = [20,10,9,7,4,3,5]
Output: 40
Explanation: We can choose nodes 0, 2, 3, and 4.
- The sum of values on the path from 0 to 4 is equal to 10.
- The sum of values on the path from 0 to 3 is equal to 10.
- The sum of values on the path from 0 to 5 is equal to 3.
- The sum of values on the path from 0 to 6 is equal to 5.
Therefore, the tree is healthy and the score is values[0] + values[2] + values[3] + values[4] = 40.
It can be shown that 40 is the maximum score obtainable after any number of operations on the tree.

 

Constraints:

  • 2 <= n <= 2 * 104
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • values.length == n
  • 1 <= values[i] <= 109
  • The input is generated such that edges represents a valid tree.

Solutions

Solution 1: Tree DP

The problem is actually asking us to select some nodes from all nodes of the tree so that the sum of these nodes' values is maximized, and there is one node on each path from the root node to the leaf node that is not selected.

We can use the method of tree DP to solve this problem.

We design a function $dfs(i, fa)$, where $i$ represents the current node with node $i$ as the root of the subtree, and $fa$ represents the parent node of $i$. The function returns an array of length $2$, where $[0]$ represents the sum of the values of all nodes in the subtree, and $[1]$ represents the maximum value of the subtree satisfying that there is one node not selected on each path.

The value of $[0]$ can be obtained directly by DFS accumulating the values of each node, while the value of $[1]$ needs to consider two situations, namely whether node $i$ is selected. If it is selected, then each subtree of node $i$ must satisfy that there is one node not selected on each path; if it is not selected, then all nodes of each subtree of node $i$ can be selected. We take the maximum of these two situations.

It should be noted that the value of $[1]$ of the leaf node is $0$, because the leaf node has no subtree, so there is no need to consider the situation where there is one node not selected on each path.

The answer is $dfs(0, -1)[1]$.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes.

Python3

class Solution:
    def maximumScoreAfterOperations(
        self, edges: List[List[int]], values: List[int]
    ) -> int:
        def dfs(i: int, fa: int = -1) -> (int, int):
            a = b = 0
            leaf = True
            for j in g[i]:
                if j != fa:
                    leaf = False
                    aa, bb = dfs(j, i)
                    a += aa
                    b += bb
            if leaf:
                return values[i], 0
            return values[i] + a, max(values[i] + b, a)

        g = [[] for _ in range(len(values))]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        return dfs(0)[1]

Java

class Solution {
    private List<Integer>[] g;
    private int[] values;

    public long maximumScoreAfterOperations(int[][] edges, int[] values) {
        int n = values.length;
        g = new List[n];
        this.values = values;
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        return dfs(0, -1)[1];
    }

    private long[] dfs(int i, int fa) {
        long a = 0, b = 0;
        boolean leaf = true;
        for (int j : g[i]) {
            if (j != fa) {
                leaf = false;
                var t = dfs(j, i);
                a += t[0];
                b += t[1];
            }
        }
        if (leaf) {
            return new long[] {values[i], 0};
        }
        return new long[] {values[i] + a, Math.max(values[i] + b, a)};
    }
}

C++

class Solution {
public:
    long long maximumScoreAfterOperations(vector<vector<int>>& edges, vector<int>& values) {
        int n = values.size();
        vector<int> g[n];
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].emplace_back(b);
            g[b].emplace_back(a);
        }
        using ll = long long;
        function<pair<ll, ll>(int, int)> dfs = [&](int i, int fa) -> pair<ll, ll> {
            ll a = 0, b = 0;
            bool leaf = true;
            for (int j : g[i]) {
                if (j != fa) {
                    auto [aa, bb] = dfs(j, i);
                    a += aa;
                    b += bb;
                    leaf = false;
                }
            }
            if (leaf) {
                return {values[i], 0LL};
            }
            return {values[i] + a, max(values[i] + b, a)};
        };
        auto [_, b] = dfs(0, -1);
        return b;
    }
};

Go

func maximumScoreAfterOperations(edges [][]int, values []int) int64 {
	g := make([][]int, len(values))
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	var dfs func(int, int) (int64, int64)
	dfs = func(i, fa int) (int64, int64) {
		a, b := int64(0), int64(0)
		leaf := true
		for _, j := range g[i] {
			if j != fa {
				leaf = false
				aa, bb := dfs(j, i)
				a += aa
				b += bb
			}
		}
		if leaf {
			return int64(values[i]), int64(0)
		}
		return int64(values[i]) + a, max(int64(values[i])+b, a)
	}
	_, b := dfs(0, -1)
	return b
}

TypeScript

function maximumScoreAfterOperations(edges: number[][], values: number[]): number {
    const g: number[][] = Array.from({ length: values.length }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    const dfs = (i: number, fa: number): [number, number] => {
        let [a, b] = [0, 0];
        let leaf = true;
        for (const j of g[i]) {
            if (j !== fa) {
                const [aa, bb] = dfs(j, i);
                a += aa;
                b += bb;
                leaf = false;
            }
        }
        if (leaf) {
            return [values[i], 0];
        }
        return [values[i] + a, Math.max(values[i] + b, a)];
    };
    return dfs(0, -1)[1];
}