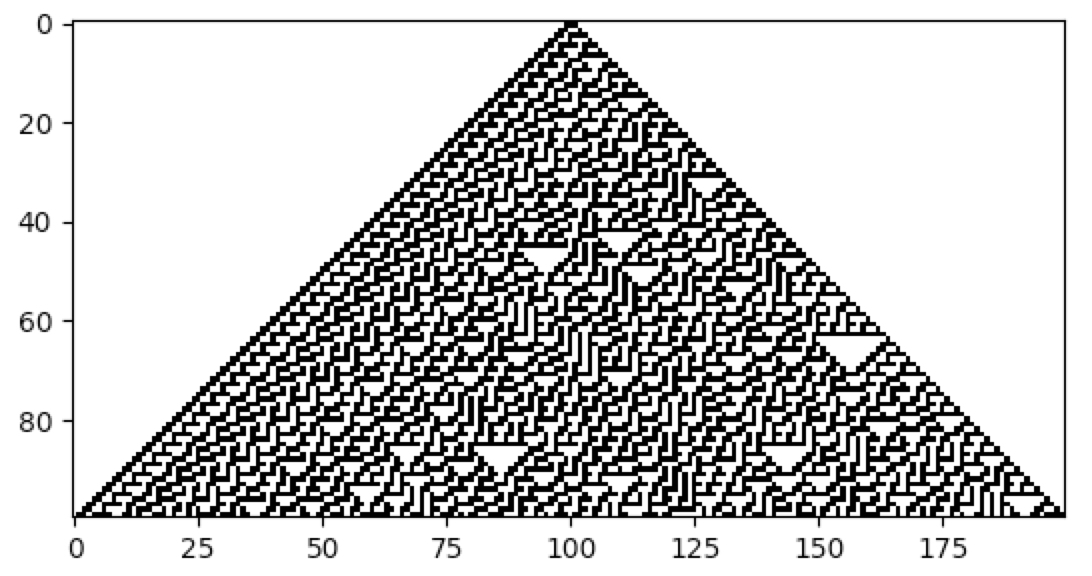
CellPyLib is a library for working with Cellular Automata, for Python. Currently, only 1- and 2-dimensional k-color cellular automata with periodic boundary conditions are supported. The size of the neighbourhood can be adjusted. While cellular automata constitute a very broad class of models, this library focuses on those that are constrained to a regular array or uniform grid, such as elementary CA, and 2D CA with Moore or von Neumann neighbourhoods. The cellular automata produced by this library match the corresponding cellular automata available at atlas.wolfram.com.
Example usage:
import cellpylib as cpl
# initialize a CA with 200 cells (a random initialization is also available)
cellular_automaton = cpl.init_simple(200)
# evolve the CA for 100 time steps, using Rule 30 as defined in NKS
cellular_automaton = cpl.evolve(cellular_automaton, timesteps=100, memoize=True,
apply_rule=lambda n, c, t: cpl.nks_rule(n, 30))
# plot the resulting CA evolution
cpl.plot(cellular_automaton)You should use CellPyLib if:
- you are an instructor or student wishing to learn more about Elementary Cellular Automata and 2D Cellular Automata on a uniform grid (such as the Game of Life, the Abelian sandpile, Langton's Loops, etc.)
- you are a researcher who wishes to work with Elementary Cellular Automata and/or 2D Cellular Automata on a uniform grid, and would like to use a flexible, correct and tested library that provides access to such models as part of your research
If you would like to work with Cellular Automata on arbitrary networks (i.e. non-uniform grids), have a look at the Netomaton project. If you would like to work with 3D CA, have a look at the CellPyLib-3d project.
CellPyLib can be installed via pip:
pip install cellpylib
Requirements for using this library are Python 3.6, NumPy, and Matplotlib. Have a look at the documentation, located at cellpylib.org, for more information.
The size of the cell neighbourhood can be varied by setting the parameter r when calling the evolve function. The
value of r represents the number of cells to the left and to the right of the cell under consideration. Thus, to
get a neighbourhood size of 3, r should be 1, and to get a neighbourhood size of 7, r should be 3.
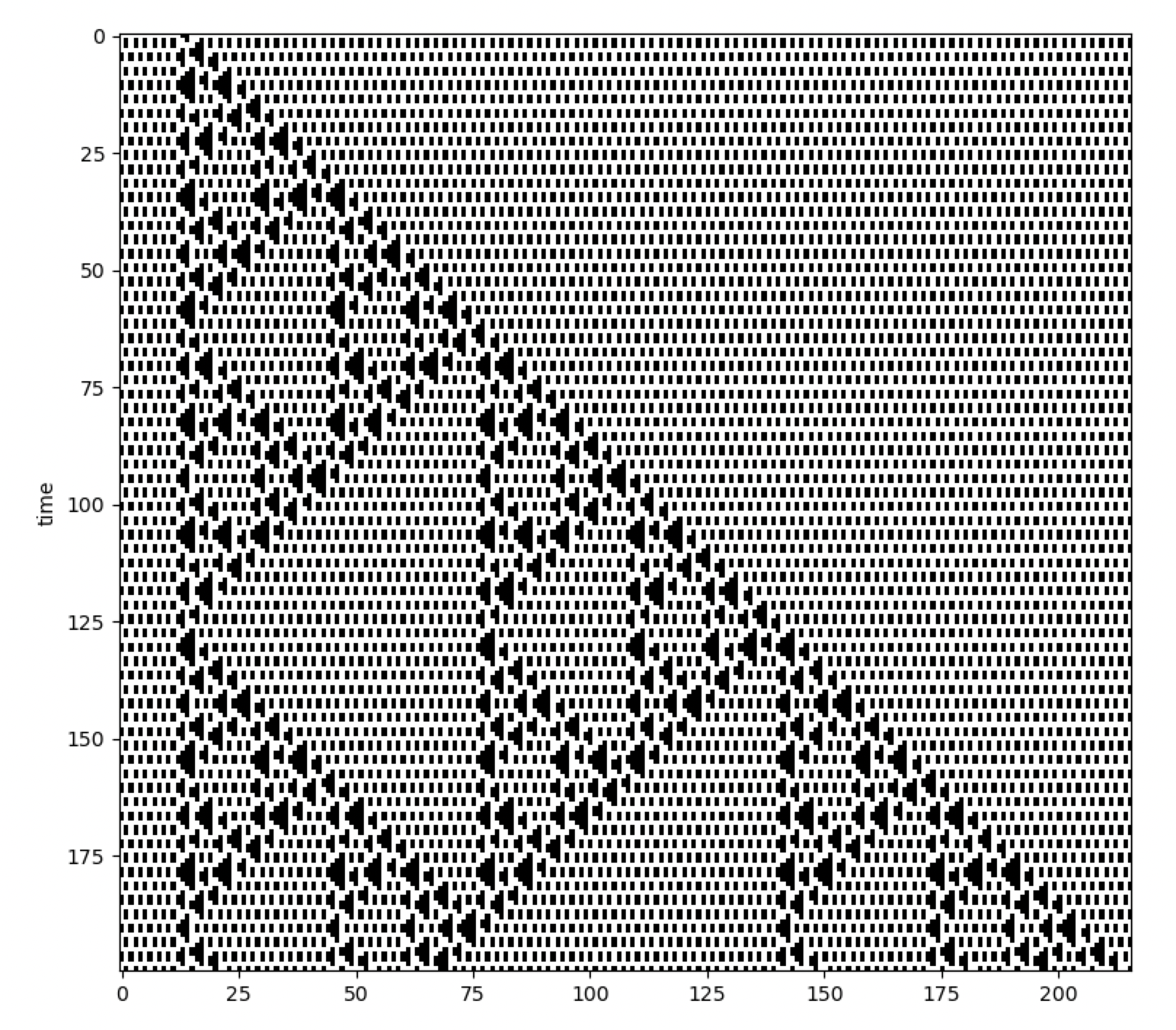
As an example, consider the work of M. Mitchell et al., carried out in the 1990s, involving the creation (discovery) of
a cellular automaton that solves the density classification problem: if the initial random binary vector contains
more than 50% of 1s, then a cellular automaton that solves this problem will give rise to a vector that contains only
1s after a fixed number of time steps, and likewise for the case of 0s. A very effective cellular automaton that solves
this problem most of the time was found using a Genetic Algorithm.
import cellpylib as cpl
cellular_automaton = cpl.init_random(149)
# Mitchell et al. discovered this rule using a Genetic Algorithm
rule_number = 6667021275756174439087127638698866559
# evolve the CA, setting r to 3, for a neighbourhood size of 7
cellular_automaton = cpl.evolve(cellular_automaton, timesteps=149,
apply_rule=lambda n, c, t: cpl.binary_rule(n, rule_number), r=3)
cpl.plot(cellular_automaton)For more information, see:
Melanie Mitchell, James P. Crutchfield, and Rajarshi Das, "Evolving Cellular Automata with Genetic Algorithms: A Review of Recent Work", In Proceedings of the First International Conference on Evolutionary Computation and Its Applications (EvCA'96), Russian Academy of Sciences (1996).
The number of states, or colors, that a cell can adopt is given by k. For example, a binary cellular automaton, in which a cell can
assume only values of 0 and 1, has k = 2. CellPyLib supports any value of k. A built-in function, totalistic_rule,
is an implementation of the Totalistic cellular automaton rule,
as described in Wolfram's NKS. The code snippet below illustrates using this rule.
A value of k of 3 is used, but any value between (and including) 2 and 36 is currently supported. The rule number is
given in base 10 but is interpreted as the rule in base k (thus rule 777 corresponds to '1001210' when k = 3).
import cellpylib as cpl
cellular_automaton = cpl.init_simple(200)
# evolve the CA, using totalistic rule 777 for a 3-color CA
cellular_automaton = cpl.evolve(cellular_automaton, timesteps=100,
apply_rule=lambda n, c, t: cpl.totalistic_rule(n, k=3, rule=777))
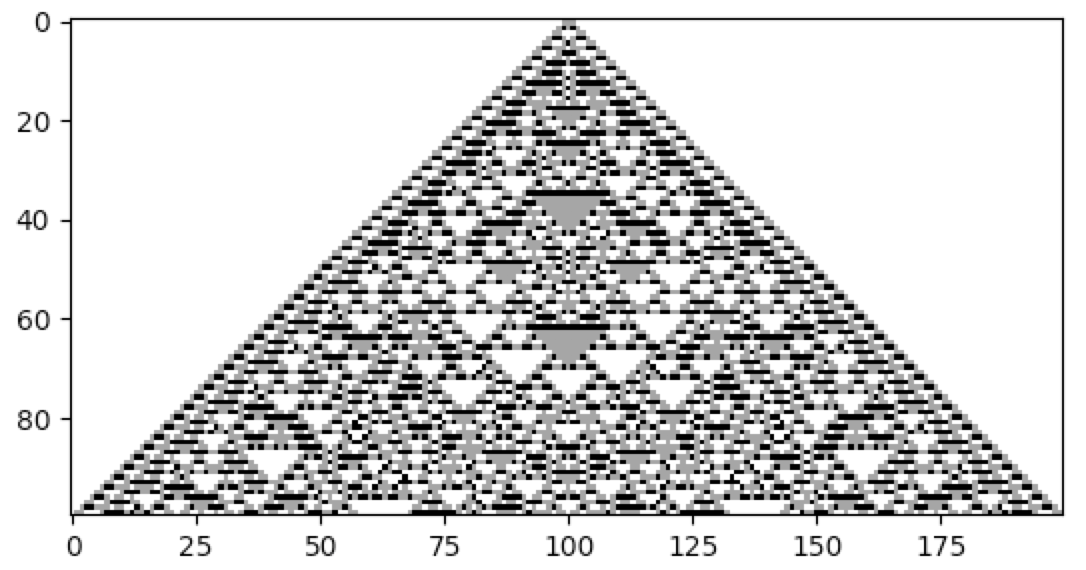
cpl.plot(cellular_automaton)One way to specify cellular automata rules is with rule tables. Rule tables are enumerations of all possible neighbourhood states together with their cell state mappings. For any given neighbourhood state, a rule table provides the associated cell state value. CellPyLib provides a built-in function for creating random rule tables. The following snippet demonstrates its usage:
import cellpylib as cpl
rule_table, actual_lambda, quiescent_state = cpl.random_rule_table(lambda_val=0.45, k=4, r=2,
strong_quiescence=True, isotropic=True)
cellular_automaton = cpl.init_random(128, k=4)
# use the built-in table_rule to use the generated rule table
cellular_automaton = cpl.evolve(cellular_automaton, timesteps=200,
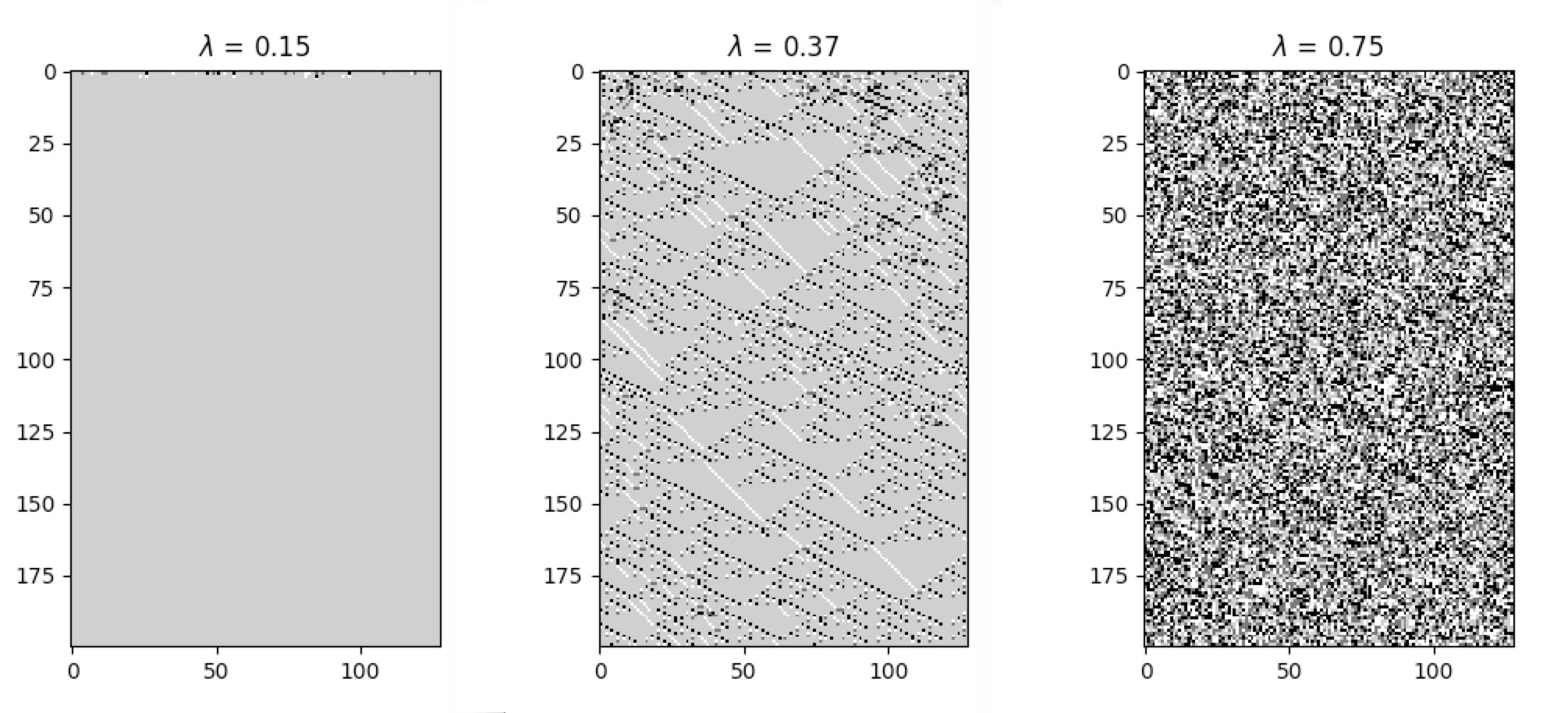
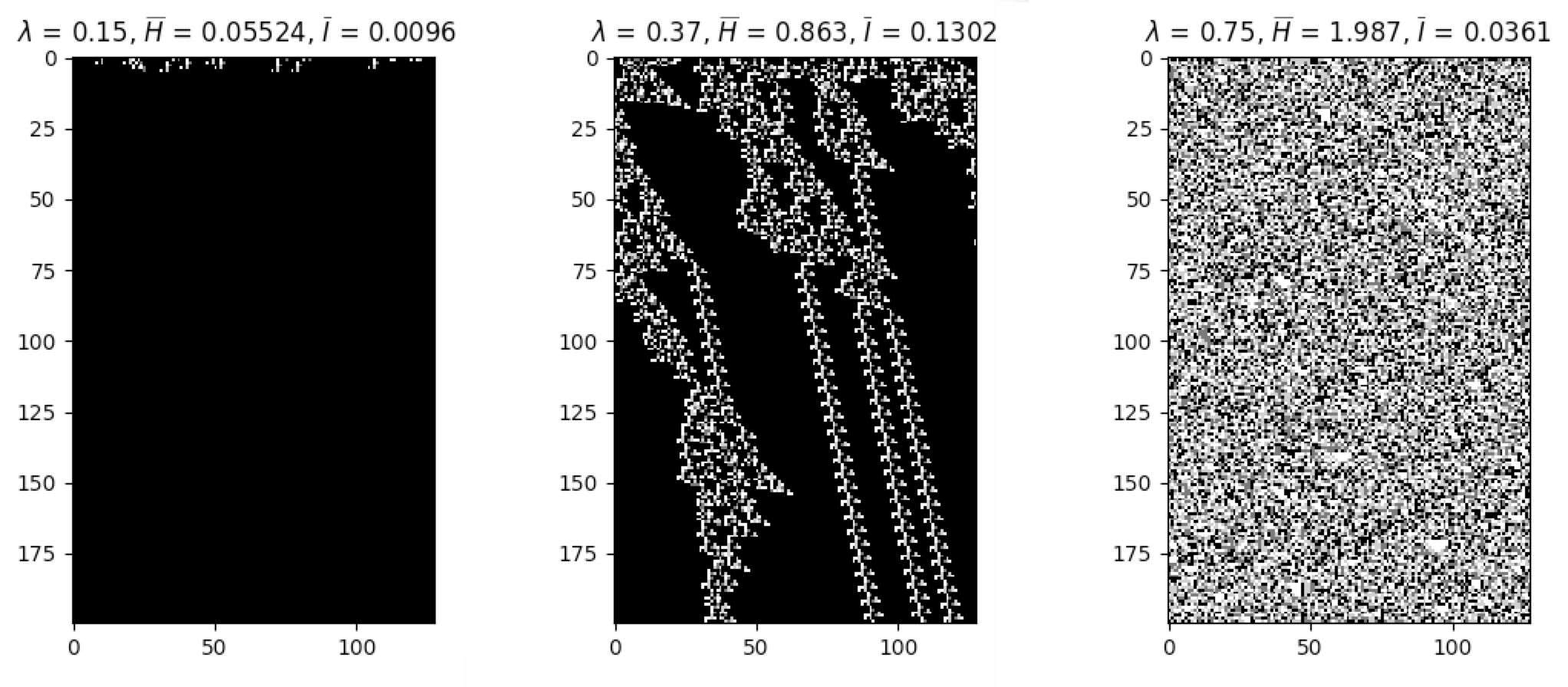
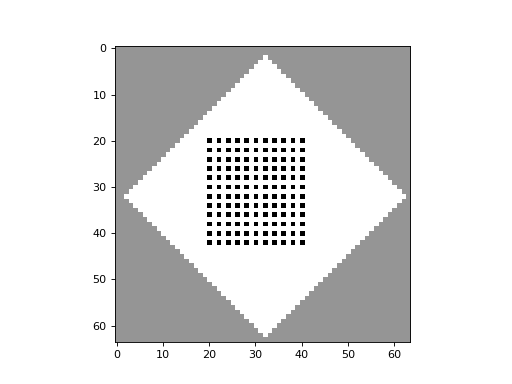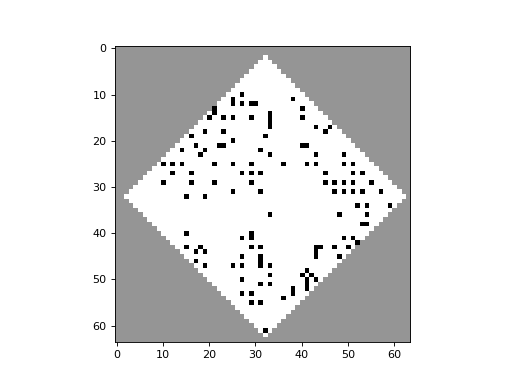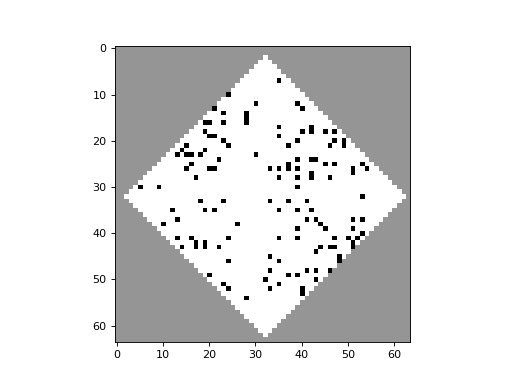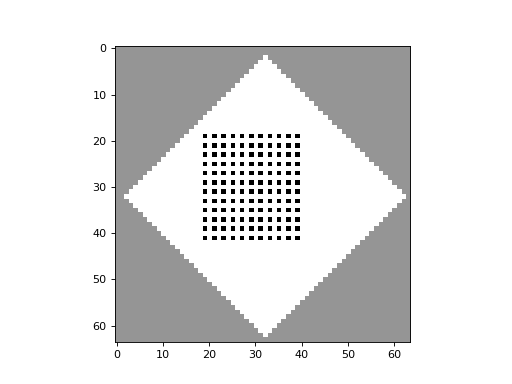
apply_rule=lambda n, c, t: cpl.table_rule(n, rule_table), r=2)The following plots demonstrate the effect of varying the lambda parameter:
C. G. Langton describes the lambda parameter, and the transition from order to criticality to chaos in cellular automata while varying the lambda parameter, in the paper:
Langton, C. G. (1990). Computation at the edge of chaos: phase transitions and emergent computation. Physica D: Nonlinear Phenomena, 42(1-3), 12-37.
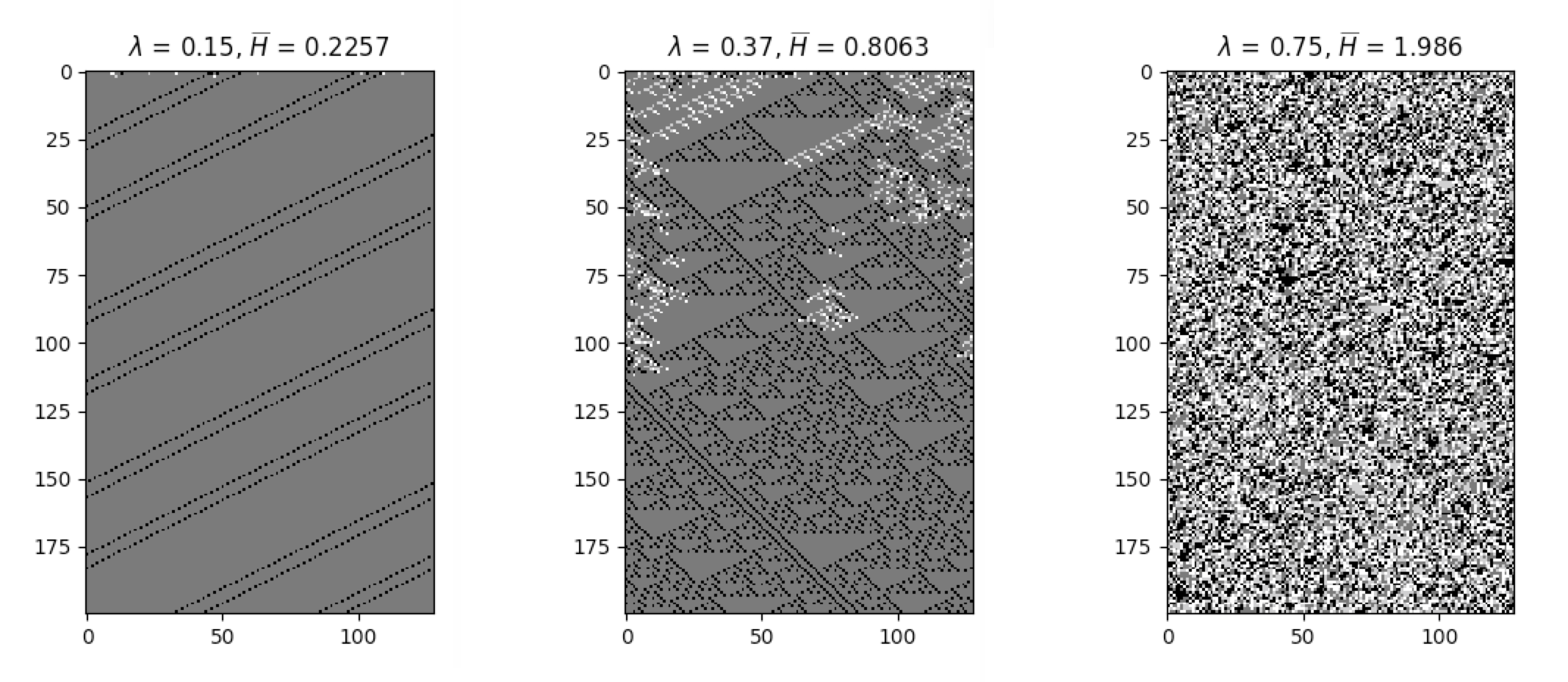
CellPyLib provides various built-in functions which can act as measures of complexity in the cellular automata being examined.
Average cell entropy can reveal something about the presence of information within cellular automata dynamics. The
built-in function average_cell_entropy provides the average Shannon entropy per single cell in a given cellular
automaton. The following snippet demonstrates the calculation of the average cell entropy:
import cellpylib as cpl
cellular_automaton = cpl.init_random(200)
cellular_automaton = cpl.evolve(cellular_automaton, timesteps=1000,
apply_rule=lambda n, c, t: cpl.nks_rule(n, 30))
# calculate the average cell entropy; the value will be ~0.999 in this case
avg_cell_entropy = cpl.average_cell_entropy(cellular_automaton)The following plots illustrate how average cell entropy changes as a function of lambda:
The degree to which a cell state is correlated to its state in the next time step can be described using mutual
information. Ideal levels of correlation are required for effective processing of information. The built-in function
average_mutual_information provides the average mutual information between a cell and itself in the next time step
(the temporal distance can be adjusted). The following snippet demonstrates the calculation of the average mutual
information:
import cellpylib as cpl
cellular_automaton = cpl.init_random(200)
cellular_automaton = cpl.evolve(cellular_automaton, timesteps=1000,
apply_rule=lambda n, c, t: cpl.nks_rule(n, 30))
# calculate the average mutual information between a cell and itself in the next time step
avg_mutual_information = cpl.average_mutual_information(cellular_automaton)The following plots illustrate how average mutual information changes as a function of lambda:
Elementary cellular automata can be explicitly made to be reversible. The following example demonstrates the creation of the elementary reversible cellular automaton rule 90R:
import cellpylib as cpl
cellular_automaton = cpl.init_random(200)
rule = cpl.ReversibleRule(cellular_automaton[0], 90)
cellular_automaton = cpl.evolve(cellular_automaton, timesteps=100,
apply_rule=rule)
cpl.plot(cellular_automaton)In addition to discrete values, cellular automata can assume continuous values. CellPyLib supports
continuous-valued automata. To create cellular automata with continuous values--or any kind of data type--simply
specify the dtype parameter when invoking any of the init and evolve built-in functions. For example, to create
a cellular automata with continuous values, one might specify the following parameter: dtype=np.float32.
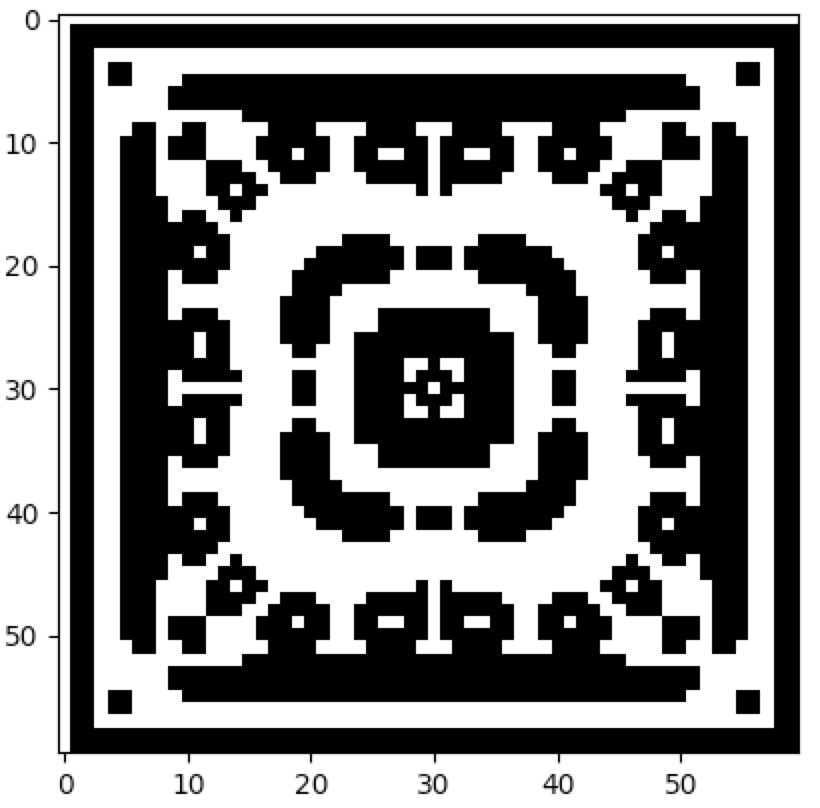
CellPyLib supports 2-dimensional cellular automata with periodic boundary conditions. The number of states, k, can be any whole number. The neighbourhood radius, r, can also be any whole number, and both Moore and von Neumann neighbourhood types are supported. The following snippet demonstrates creating a 2D totalistic cellular automaton:
import cellpylib as cpl
# initialize a 60x60 2D cellular automaton
cellular_automaton = cpl.init_simple2d(60, 60)
# evolve the cellular automaton for 30 time steps,
# applying totalistic rule 126 to each cell with a Moore neighbourhood
cellular_automaton = cpl.evolve2d(cellular_automaton, timesteps=30, neighbourhood='Moore',
apply_rule=lambda n, c, t: cpl.totalistic_rule(n, k=2, rule=126))
cpl.plot2d(cellular_automaton)The plot2d function plots the state of the cellular automaton at the final time step:
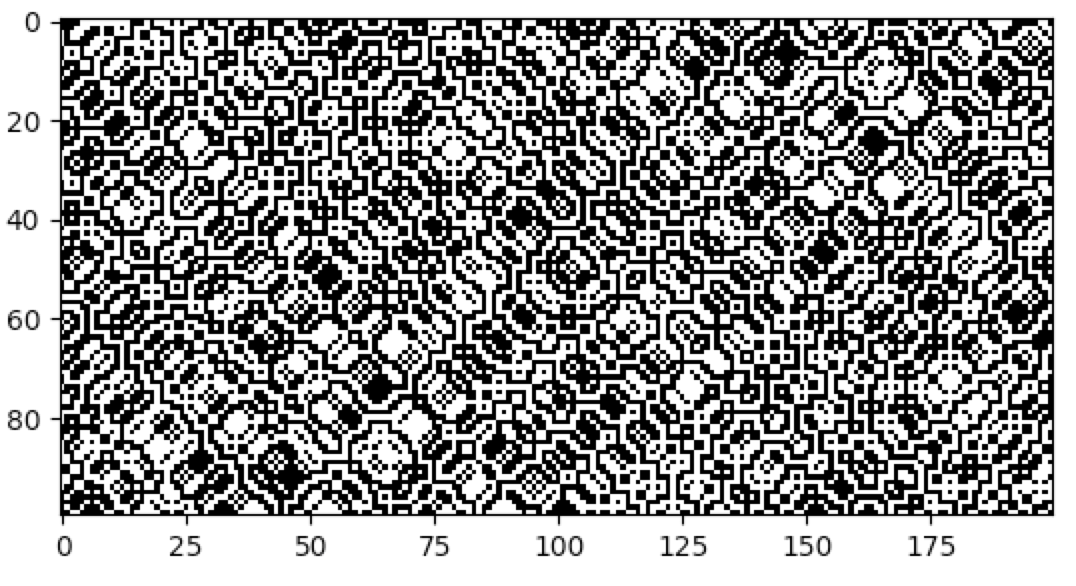
There are a number of built-in plotting functions for 2D cellular automata. For example, plot2d_animate will animate
the evolution of the cellular automaton. This is illustrated in the following snippet, which demonstrates the built-in
Game of Life rule:
import cellpylib as cpl
# Glider
cellular_automaton = cpl.init_simple2d(60, 60)
cellular_automaton[:, [28,29,30,30], [30,31,29,31]] = 1
# Blinker
cellular_automaton[:, [40,40,40], [15,16,17]] = 1
# Light Weight Space Ship (LWSS)
cellular_automaton[:, [18,18,19,20,21,21,21,21,20], [45,48,44,44,44,45,46,47,48]] = 1
# evolve the cellular automaton for 60 time steps
cellular_automaton = cpl.evolve2d(cellular_automaton, timesteps=60, neighbourhood='Moore',
apply_rule=cpl.game_of_life_rule, memoize='recursive')
cpl.plot2d_animate(cellular_automaton)For more information about Conway's Game of Life, see:
Conway, J. (1970). The game of life. Scientific American, 223(4), 4.
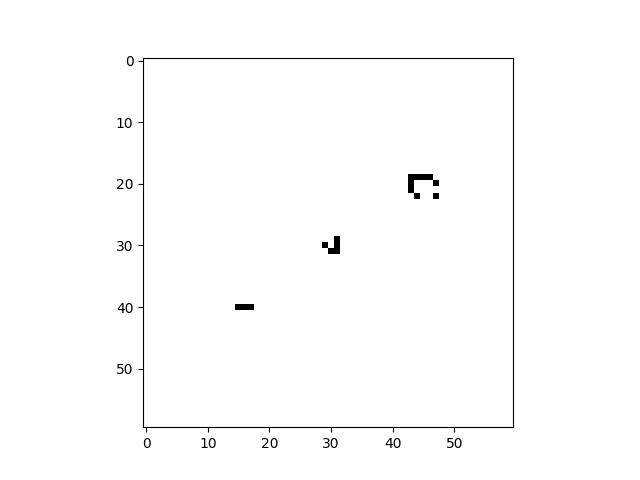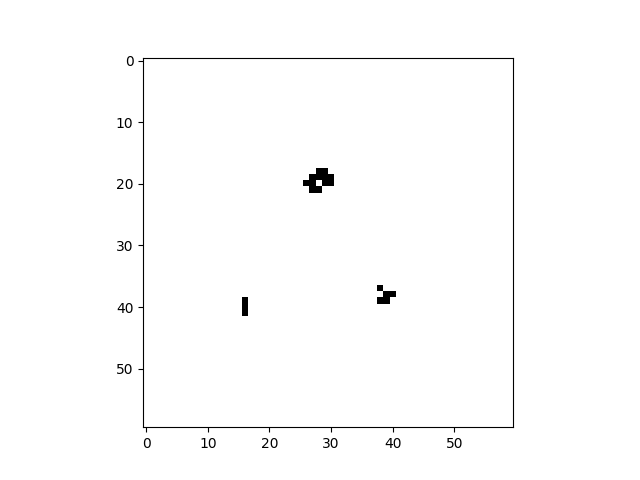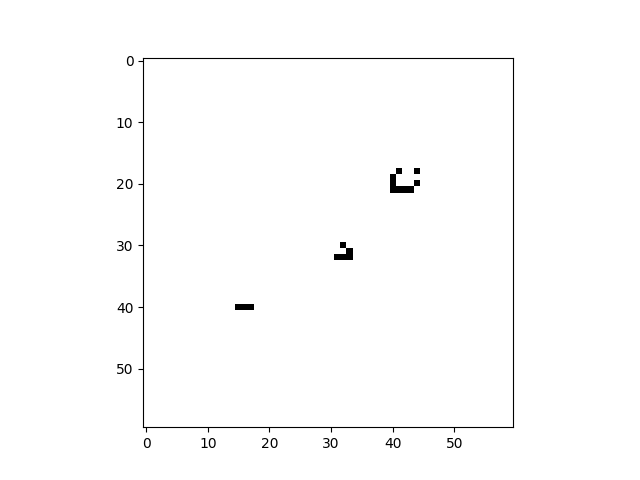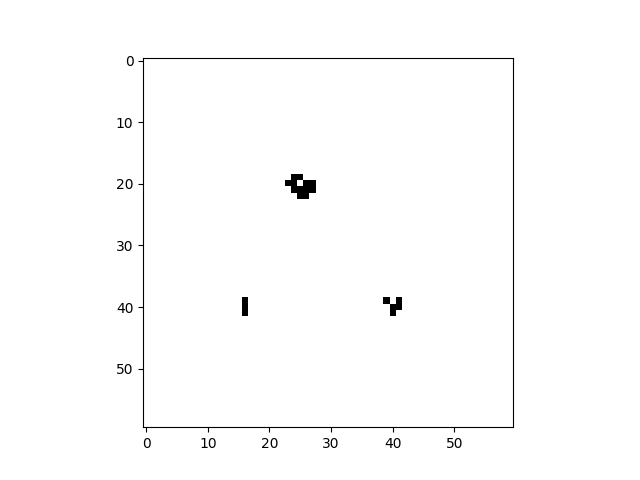
Instead of a rule applying to a single cell at a time (given its neighbourhood), a rule can apply to a block of cells, given only the states of the cells in the block. Such a system is called a block cellular automaton. For example, the following code reproduces the block CA at the bottom of page 460 of Wolfram's NKS:
import cellpylib as cpl
import numpy as np
initial_conditions = np.array([[0]*13 + [1]*2 + [0]*201])
def block_rule(n, t):
if n == (1, 1): return 1, 1
elif n == (1, 0): return 1, 0
elif n == (0, 1): return 0, 0
elif n == (0, 0): return 0, 1
ca = cpl.evolve_block(initial_conditions, block_size=2,
timesteps=200, apply_rule=block_rule)
cpl.plot(ca)Block cellular automata can also exist in 2 dimensions, as the following example demonstrates:
The full source code for this example can be found here.
Memoization is expected to provide an increase to execution speed when there is some overhead involved when invoking the rule. Only stateless rules that depend only on the cell neighbourhood are supported. Consider the following example of rule 30, where memoization is enabled:
import cellpylib as cpl
import time
start = time.time()
cpl.evolve(cpl.init_simple(1000), timesteps=500,
apply_rule=lambda n, c, t: cpl.nks_rule(n, 30), memoize=True)
print(f"Elapsed: {time.time() - start:.2f} seconds")The program above prints Elapsed: 0.33 seconds (actual execution time may vary, depending on the device used).
Without memoization, the program requires approximately 23 seconds to complete.
Create a Conda environment from the provided environment YAML file:
$ conda env create -f environment.yml
Documentation
To build the Sphinx documentation locally, from the doc directory:
$ make clean html
The generated files will be in _build/html.
To build the documentation for publication, from the doc directory:
$ make github
The generated files will be in _build/html and in the site/docs folder.
Testing
There are a number of unit tests for this project. To run the tests:
$ python -m pytest tests
If the pytest-cov package is installed, a coverage report can be generated by running the tests with:
$ python -m pytest tests/ --cov=cellpylib
If you have any questions or comments, or if you find any bugs, please open an issue in this project. Please feel free to fork the project, and create a pull request, if you have any improvements or bug fixes. We welcome all feedback and contributions.
This project has been published in the Journal of Open Source Software. This project may be cited as:
Antunes, L. M. (2021). CellPyLib: A Python Library for working with Cellular Automata. Journal of Open Source Software, 6(67), 3608.
BibTeX:
@article{Antunes2021,
doi = {10.21105/joss.03608},
url = {https://doi.org/10.21105/joss.03608},
year = {2021},
publisher = {The Open Journal},
volume = {6},
number = {67},
pages = {3608},
author = {Luis M. Antunes},
title = {CellPyLib: A Python Library for working with Cellular Automata},
journal = {Journal of Open Source Software}
}
Please star this repository if you find it useful, or use it as part of your research.