递归Recursion.md

递归需要满足的三个条件

1. 一个问题可以分解为几个子问题的解

2. 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样

3. 存在递归终止条件

如何编写递归代码

写出递推公式，找到终止条件

以爬梯子问题为例，假如这里有 n 个台阶，每次可以跨 1 个台阶或者 2 个台阶，请问走这 n 个台阶有多少种走法？

仔细思考，在第 n 个台阶的走法有两种，一种是走 1 阶，合计走法就是在 n - 1 个台阶的走法加上这一次这种；一种是走 2 阶，合计走法就是在 n - 2 个台阶的走法加上这一次这种。用公式表示就是：

f(n) = f(n - 1) + f(n - 2)

有了递推公式，再来找终止条件。当 n = 1 时，只有一种走法，f(1) = 1，当 n = 2 时，有两种走法，f(2) = 2。

合并递推公式和终止条件

int f(int n){
	if(n == 1) return 1;
  if(n == 2) return 2;
  return f(n - 1) + f(n - 2);
}

总结一下，写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。

对于递归代码，这种试图想清楚整个递和归过程的做法，实际上是进入了一个思维误区，很多时候理解起来都会比较吃力，给自己制造了理解障碍。

正确的思维方式应该是，如何一个问题 A 可以拆分为若干个子问题 B、C、D，可以假设 B、C、D 已经解决，在此基础上思考如何解决问题 A。而且只需要考虑 A 与 B、C、D 两层之间的关系即可，不需要一层一层去思考，计算机擅长做这些，人不擅长。

因此，编写递归代码的关键是，只要遇到递归，把它抽象成一个递推公式，不用想一层层的调用关系，不要试图用人脑去分解递归的每个步骤。

递归代码要警惕堆栈溢出

在实际开发中，编写递归代码时，我们会遇到很多问题。比如堆栈溢出。而堆栈溢出会造成系统性崩溃，后果非常严重。

递归代码要警惕重复计算

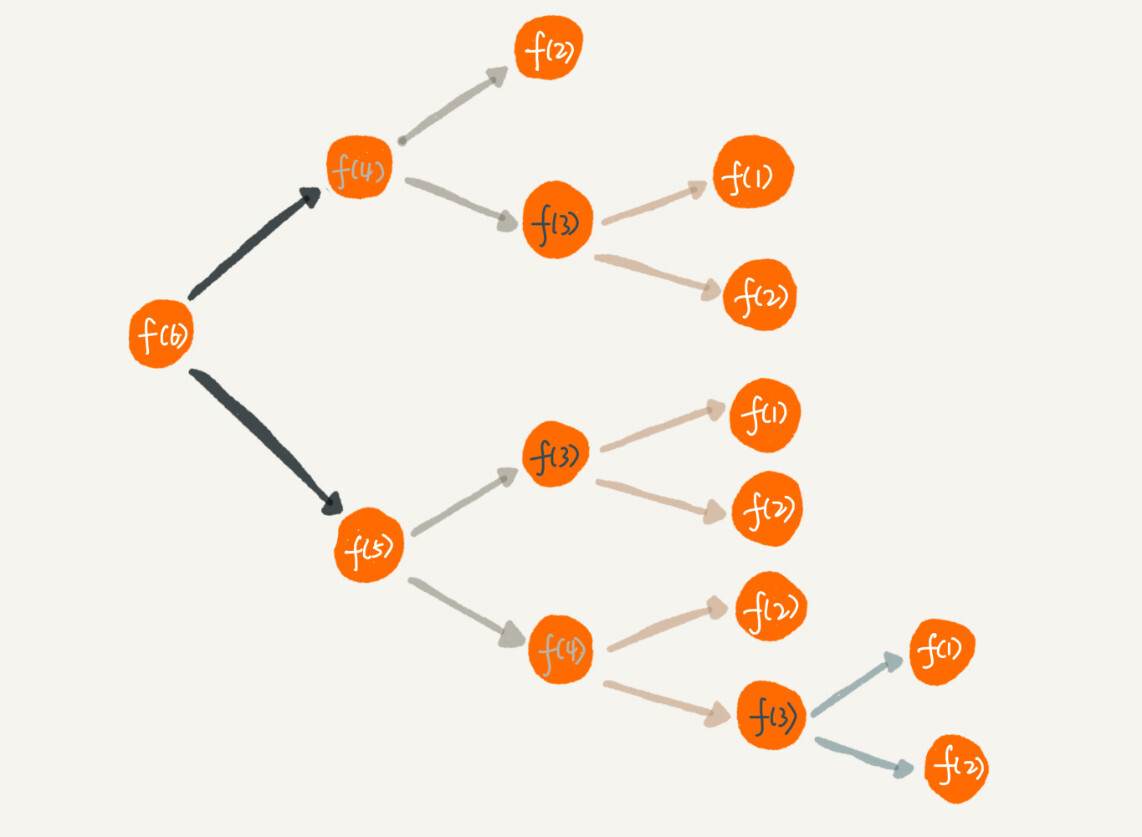
之前爬梯子的问题中，我们把递归过程分解一下

从图中可以很直观的发现，f(3) 与 f(4) 被计算了多次，这就是重复计算问题。

为了避免重复计算，我们可以通过一个数据结果（比如散列表）来保存已经求解过的 f(k)，这样当递归调用到 f(k) 时，就不需要重复计算就可以直接取值了。

public int f(int n){
  if(n == 1) return 1;
  if(n == 2) return 2;
  
  // hasSolvedList 可以理解为一个 Map，key 是 n，value 是 f(n)
  if(hasSolvedList.containsKey(n)){
    return hasSolvedList.get(n);
  }
  
  int ret = f(n - 1) + f(n -2);
  hasSolvedList.put(n, ret);
  return ret;
}

怎么将递归代码改写为非递归代码

递归有利有弊，利是递归代码的表达能力强，写起来非常简洁；而弊就是空间复杂度高、有堆栈溢出的危险、存在重复计算、过多的函数调用会耗时较多等问题。

所以实际开发过程中，应根据实际情况来选择是否需要使用递归来实现。

f(x) = f(x - 1) + 1可以改写为

int f(int n){
  int ret = 1;
  for(int i = 2; i <=n; ++i){
    ret = ret + 1;
  }
  return ret;
}

f(n) = f(n - 1) + f(n - 2)改写为

int f(int n){
  if(n == 1) return 1;
  if(n == 2) return 2;
  int ret = 0;
  int pre = 2;
  int prepre = 1;
  for(int i = 3; i <= n; ++i){
    ret = pre + prepre;
    prepre = pre;
    pre = ret;
  }
  return ret;
}

那是不是所有递归代码都可以改为这种迭代循环的非递归代码呢？

笼统的讲是这样的。因为递归本身就是借助栈来实现的，只不过我们使用的栈是系统或者虚拟机本身提供的，我们没有感知罢了。

但这种思路实际上是将递归改为了手动递归，本质并没有变，而且也没有解决前面讲到的某些问题，徒增了实现的复杂度。