A Python3 module for the analysis, elastic contact and fluid flow simulation of rock fractures.
| Platform | CI Status | Coverage |
|---|---|---|
| Linux, Python 3.6 |  |
 |
Clone the repo and cd into it using a virtual environment
git clone https://github.com/plang85/rough_surfaces.git
cd rough_surfaces
python3 -m venv venv
source venv/bin/activate
and verify that the tests are passing
pip install -e .[test]
pytest
do some damage and just PR against master.
To just use the module, it's still good practice to checkout the repo and use a venv, but then just do
pip install .
instead. As you can see recommenden practice is to use the head at all times (if you're adventureous).
We can generate an isotropic, self-affine surface like this
import rough_surface.params as rp
import rough_surface.generate as rg
surface_params = rp.SelfAffineParameters()()
N_power_of_two = 9
surface = rg.self_affine(surface_params, N_power_of_two)
where surface is essentially a two-dimensional numpy array with a lattice size attribute dxy.
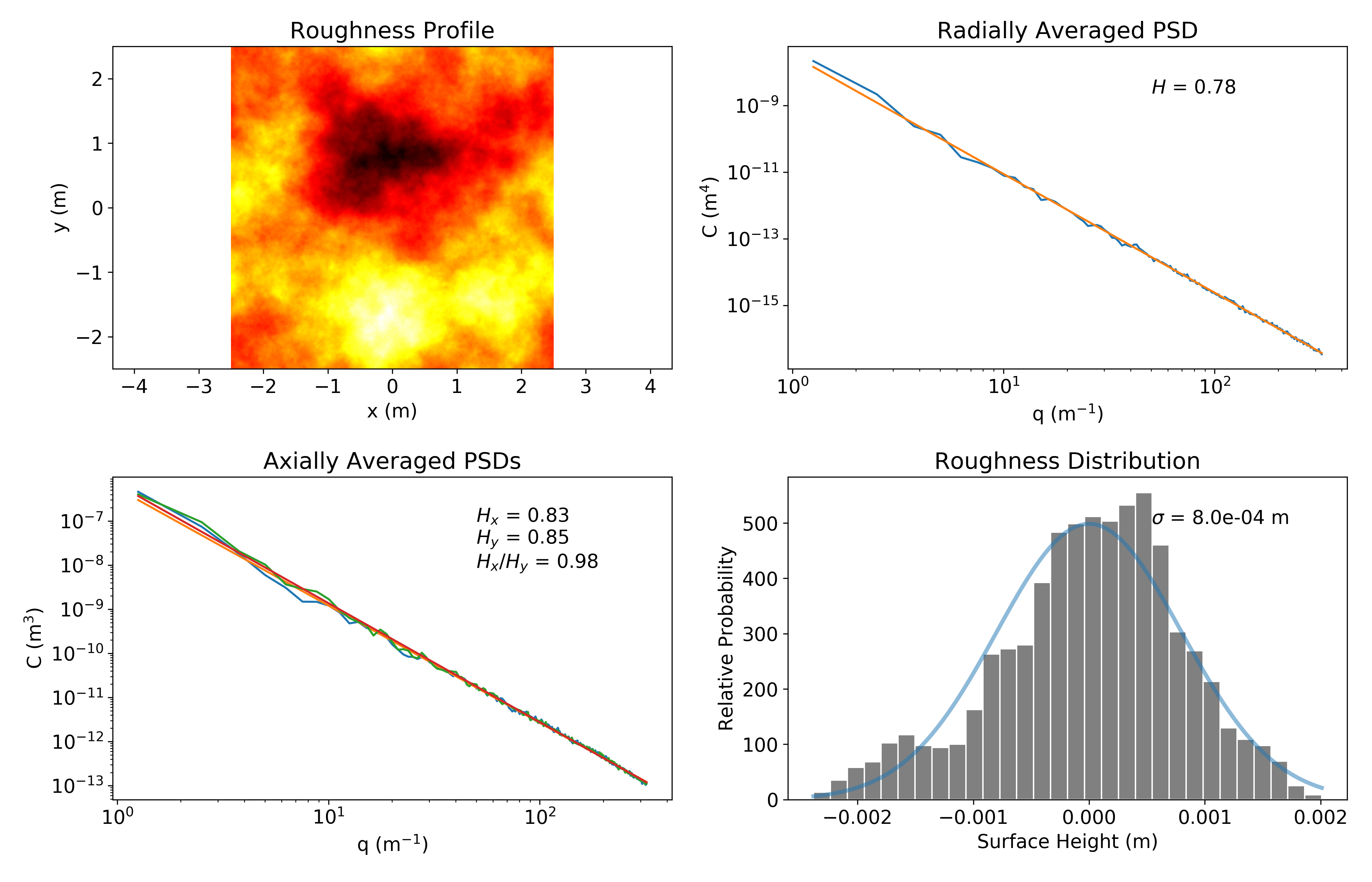
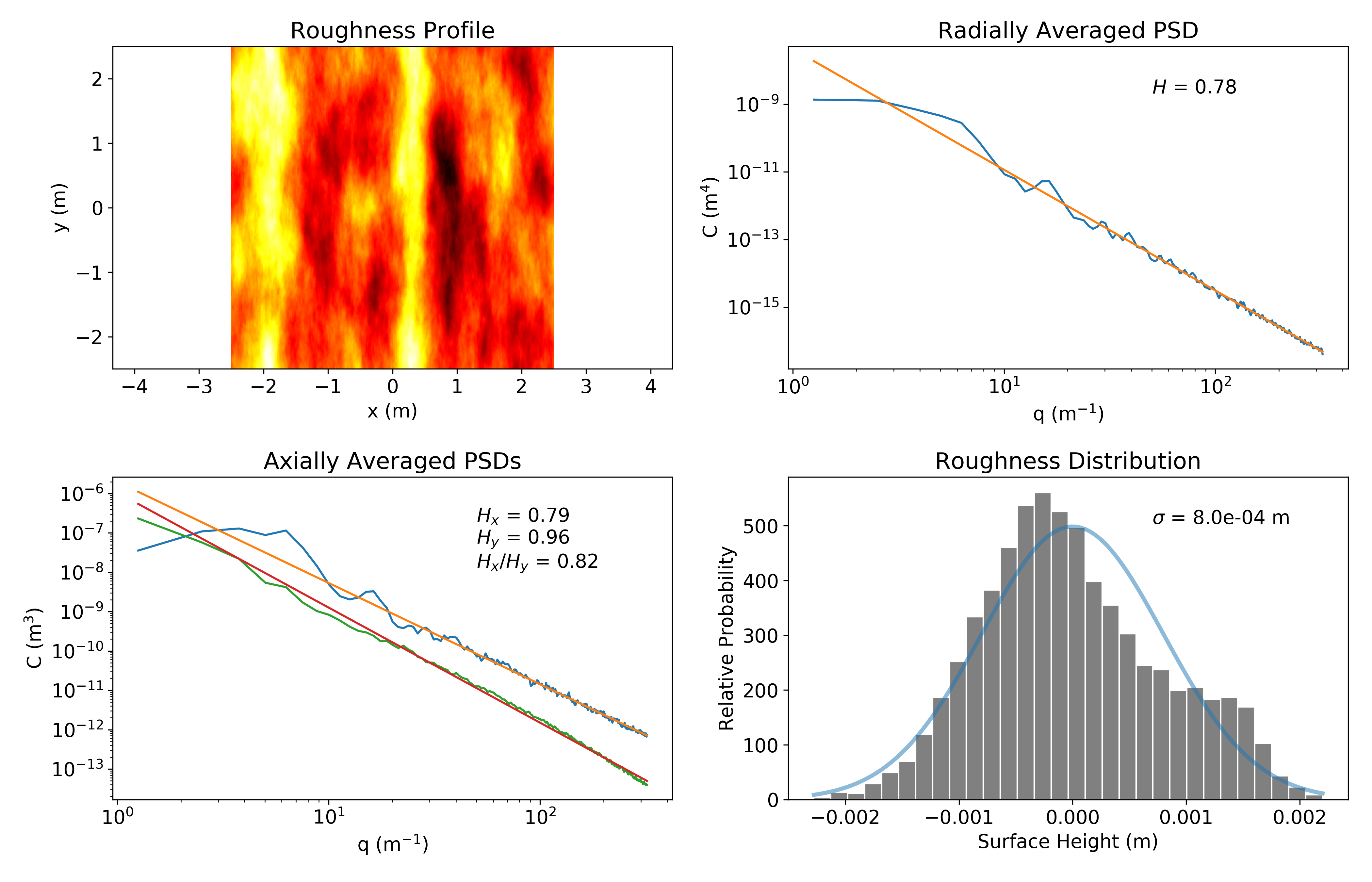
See example_analysis.py for a more complete overview and the provided plotting functions. In short, given a two-dimensional array h that represents discrete surface height uniformly spaced by dxy, the radially averaged power-spectrum can be obtained like this (this API is in flux)
import rough_surfaces.analyse as ra
spectrum = ra.radially_averaged_psd(surface)
invariants = ra.self_affine_psd_fit(*surface_spectrum)
print('Hurst = {0:.2f}'.format(invariants[1]))
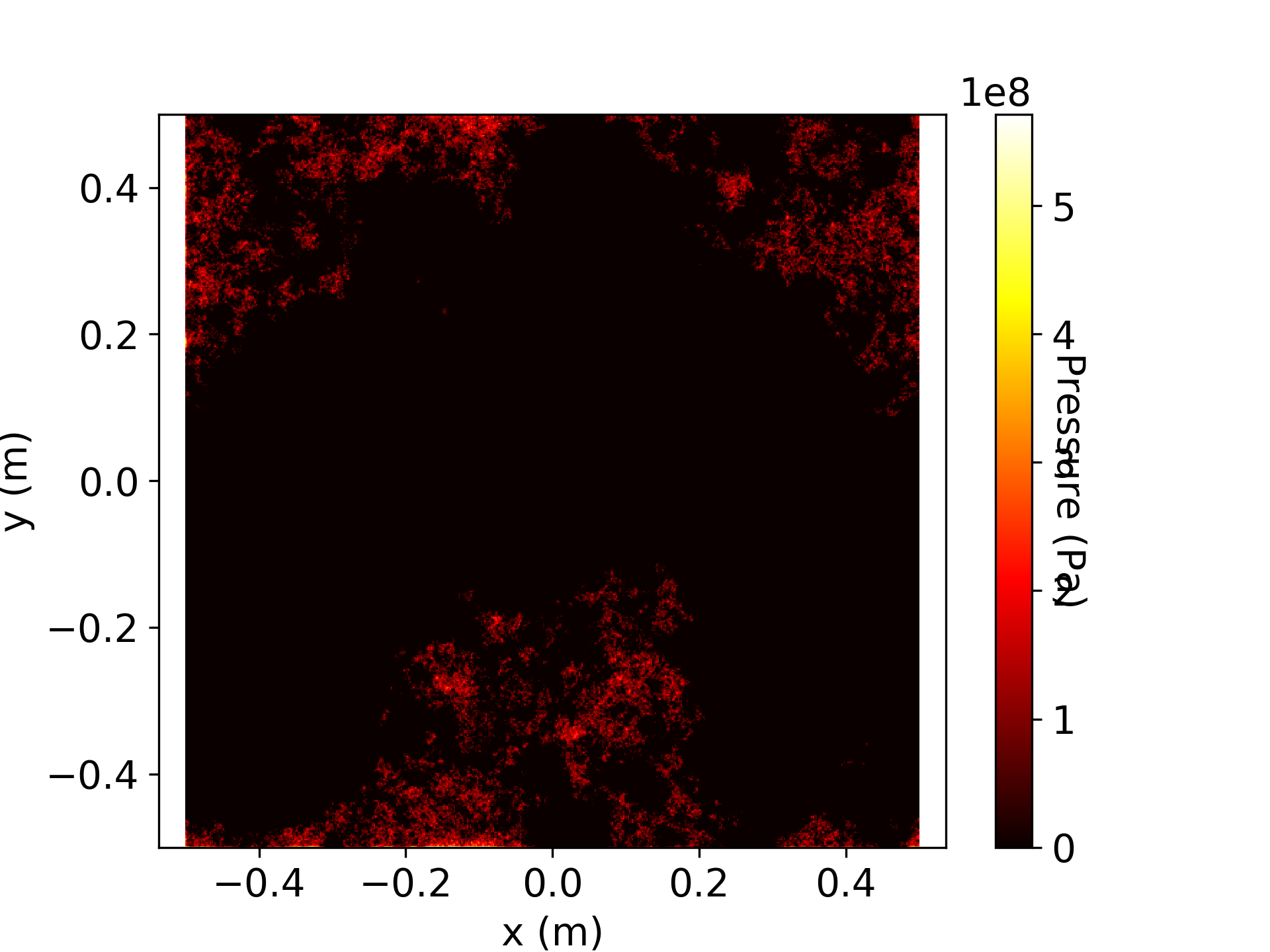
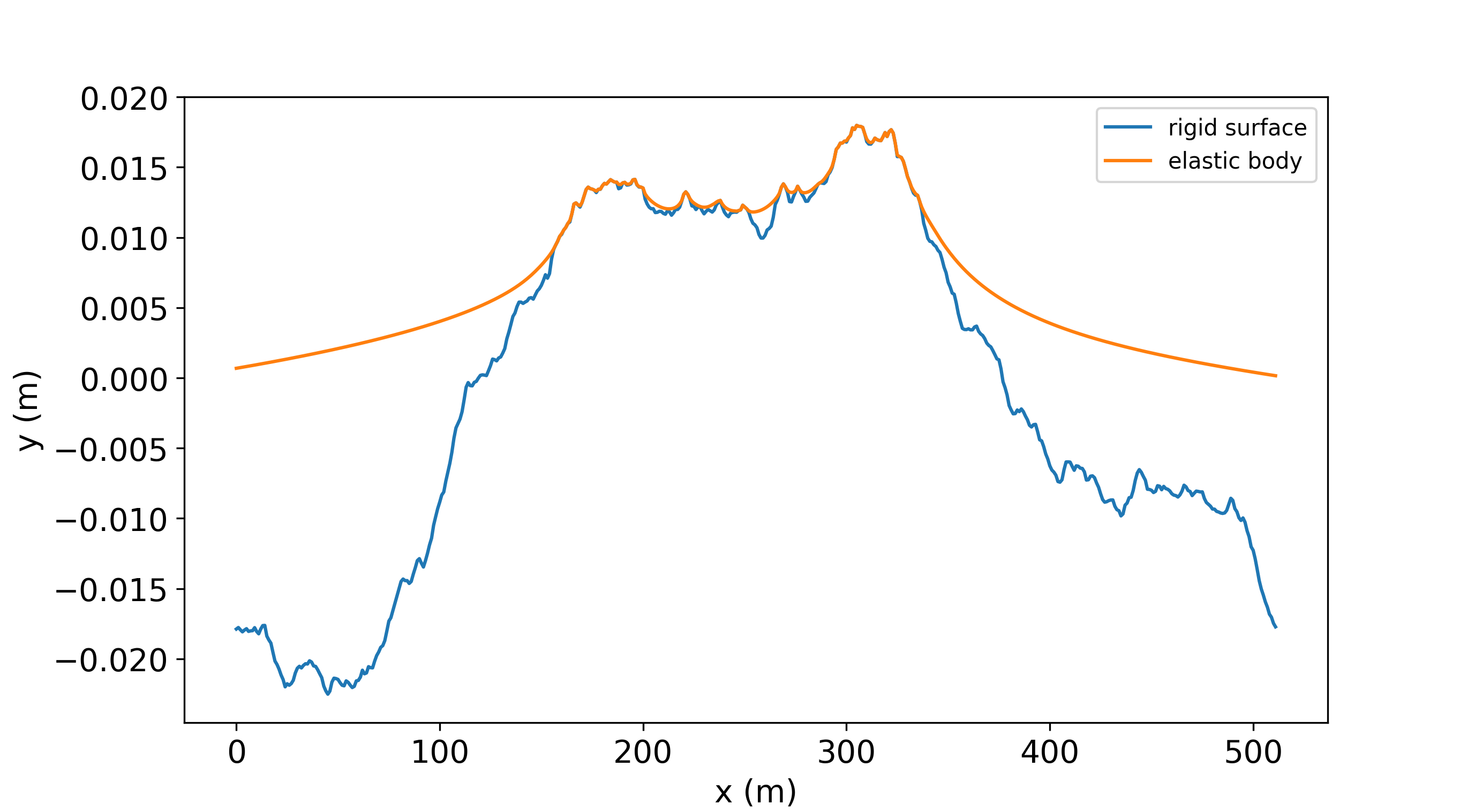
An isotropic surface is characterized by a near-ideal straight line radially averaged PSD and same-slope curves for the angularly averaged spectra.
We can solve the elastic frictionless contact between two rough surfaces by solving the equivalent problem of a rigid composite surface against an elastic, flat body of composite properties
import rough_surfaces.contact as rc
nominal_stress = 1.0E7
E = 1.0E+9
nu = 0.3
contact = rc.contact_FFT(composite_surface, nominal_stress, E, nu, verbose=1)
For a more detailed snippet see example_analysis.py.
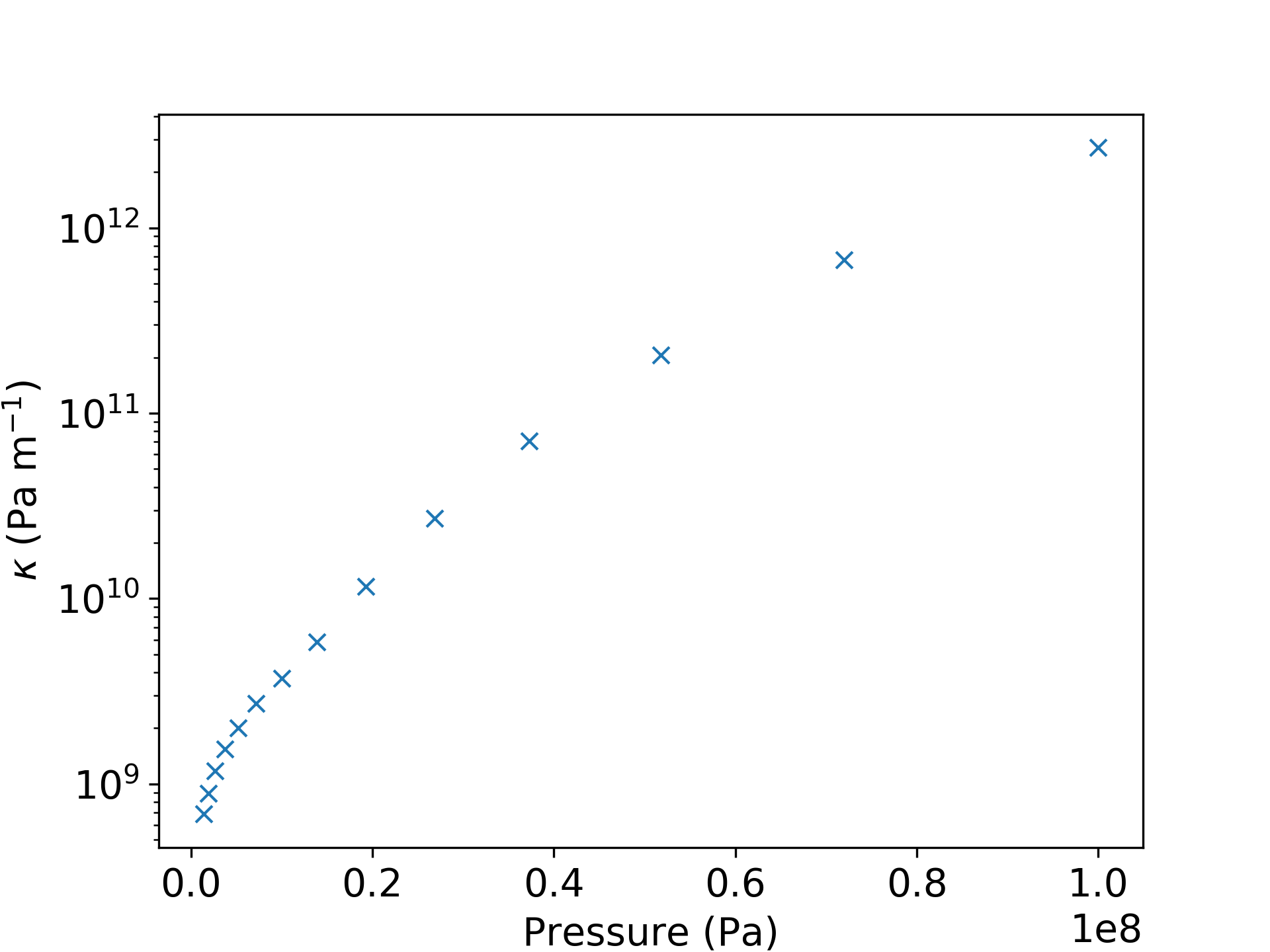
We can also use a high-level function to compute the stiffness over a range of stresses
nominal_stress = np.logspace(6, 8, 15)
stiffness = rc.stiffness(nominal_stress, surface, E, nu, err_lim=1.0E-8)
Working on porting this still...
Lang, P. S., Paluszny, A., & Zimmerman, R. W. (2015). Hydraulic sealing due to pressure solution contact zone growth in siliciclastic rock fractures. Journal of Geophysical Research: Solid Earth, 120(6), 4080–4101. http://doi.org/10.1002/2015JB011968
Lang, P. S., Paluszny, A., & Zimmerman, R. W. (2016). Evolution of fracture normal stiffness due to pressure dissolution and precipitation. International Journal of Rock Mechanics and Mining Sciences, 88, 12–22. http://doi.org/10.1016/j.ijrmms.2016.06.004
Lang, P. S. (2016). Multi-scale modelling of coupled thermo-hydro-mechanical-chemical processes in fractured rocks. Doctoral Thesis, Imperial College. http://hdl.handle.net/10044/1/45644